动态规划我理解的写法就是自底向上,自顶向下
自底向上:先初始化小问题,再层层递进,所以一般自底向上会有一步初始化
自顶向下:递归求解,但是每次求解都会存储,又叫记忆化搜索
一、小偷偷东西
问题描述:
你是一个专业的小偷,准备偷一条街上的房子,假设有四个吧,你不能偷相邻两个房子,因为这样会触发警报,所以你可以偷1和4 1和3 2和4 现在你需要做的就是偷最大值,假设每个房子的价值是{2,7,9,3,1,5,8}
自底向上算法思路:
我们先考虑只有一个房子的情况,那肯定偷
再考虑有两个房子,我们是不是要考虑偷不偷第二个房子,如果偷了,第一个房子就偷不了了,所以要比较第二个房子和第一个房子谁的价值大
那再考虑有三个房子,由于两个房子的情况已经考虑过了,所以只考虑第三个房子偷不偷,如果偷了,第二个房子就偷不了,那么此时的价值就是第三个房子的价值加第一个房子的价值,如果不偷,那是不是就等价于只考虑前两个房子的情况,这个时候把偷和不偷做比较就可以求出考虑三个房子的最大值
那么再考虑有四个房子,由于前三个房子的最优解已经考虑过了,所以这个时候只考虑第四个房子偷不偷,如果偷了第三个房子就不让偷,所以这个时候的价值就是第四个房子的价值加上只考虑前两个房子的最优解,如果不偷,那就相当于只考虑了前三个房子
大致思路如下
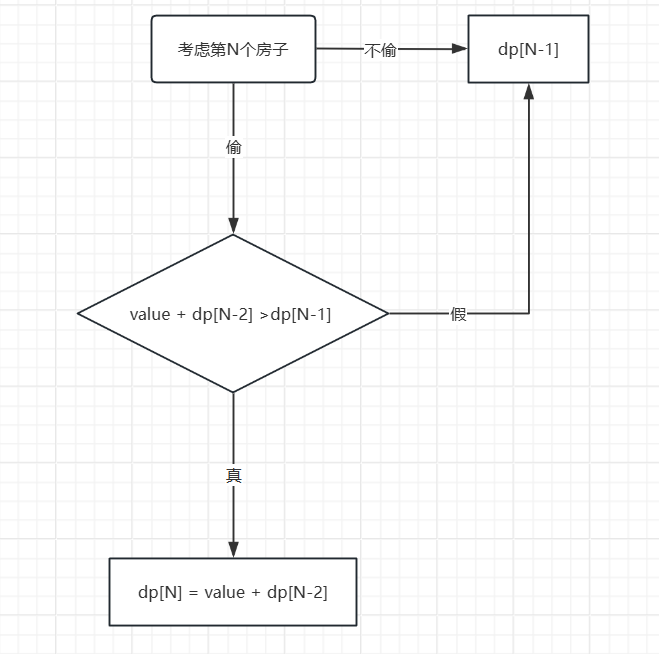
于是我们申明一个vector用来存放结果并先初始化为0,其中dp[i] 代表考虑前i个房子的情况,为什么数组长度为n+1,其实原因很简单,如果长度为n,我们想输出考虑前4个房子的最优解,是不是要输出dp[3],而不是dp[4],这样不好输出结果啊,所以就多申明了一列
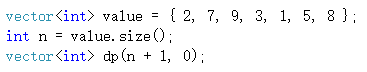
遍历房子的代码如下
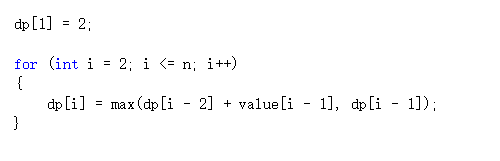
完整代码如下
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main() {
vector<int> value = { 2, 7, 9, 3, 1, 5, 8 };
int n = value.size();
vector<int> dp(n + 1, 0);
dp[1] = 2;
for (int i = 2; i <= n; i++)
{
dp[i] = max(dp[i - 2] + value[i - 1], dp[i - 1]);
}
cout << dp[n] << endl;
while (true);
}
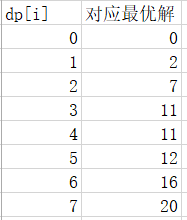
为了方便大家理解,大家自己写代码,也可以测试其中的任意一个值看看是否正确
二、01背包问题
问题描述:
当前你有一个背包重量为bagMax,有四个物品,每个物品都有自己的重量和价值,你需要考虑如何取物品才能让背包在不超容量的情况下价值最大
物品如下:
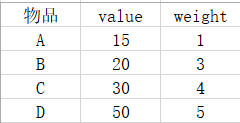
自底向上算法思路:
初始化两个数组用来存储weight 和 value
![]()
假设只考虑物品A,只需要考虑物品A放不放得进去,即 bagMax < weight 为真时候返回0,为假返回15 那么可以用一个数组存储结果 vectory<int> dp(bagMax,0),其中dp的长度是bagMax,并且每个值都初始化为0

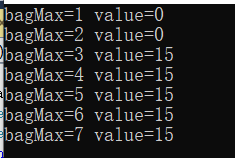
可以看到这样的写法有一个问题,由于vector访问元素的时候计数器是从0开始,我要获取bagMax=7的value的时候就得访问dp[7-1],这个地方和生活之中略有差异,生活中应该是我要获取bagMax=7的value,直接输出dp[7]就好了对吗?解决这个问题应该不难,直接多初始化一行数据就好了

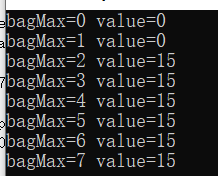
那么接下来,如果考虑物品A、B,怎么办?这个时候很容易想到用二维数组存放结果即 dp[i][j]
其中i代表考虑前i个物品,j代表bagMax=j的时候,所以dp[i][j]的意思就是说,考虑在前i个物品时,bagMax=j的时候的最优解
转换为代码就是,其中为什么wupinNums 要 +1 的理由和上面bagMax要 +1 的理由一样不再赘述了

接下来就是动态规划的思路了,先考虑第一个物品,即填充dp[1][j],思路也很简单,就是遍历bagMax,看看bagMax是不是比weight[0]大,如果大就填充其值为value[0],其实这个地方i可以从1开始,因为当i=0的时候bagMax也为0,就是说背包容量为0,那肯定是装不了东西的value一定为0,而我们初始化vector的时候已经赋值为0了,不过这里无所谓,不影响
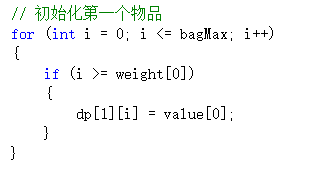
接下来就是考虑两个物品的情况,即填充dp[2][j]的值,由于第一个物品我们已经考虑过了,即dp[1][j] (j属于[0,bagMax]) 是全部已知的,所以这个时候相当于只考虑第二个物品放不放,或者说第二个物品和第一个物品只放一个的话,放哪个,或者说两个都放?
我们先说不放的情况,如果不放第二个物品,那么dp[2][j]是不是就应该等于dp[1][j],因为你不放第二个物品就完全等价于没考虑第二个物品,只考虑第一个物品
那么再说放,如果在dp[2][j]的时候要放该物品,那么背包剩余容量是不是等于 j - weight[1](这里虽然是weight[1]但是其实是第二个物品的重量),那这个剩余的容量还够不够放物品1呢?是不是值得考虑的一个事情?这个时候就是动态规划衔接上了, 即j - weight[1]放不放物品1,是不是等价于在背包容量为 j - weight[1] 时只考虑物品1的最大价值,即dp[1][j-weight[1]]的值
所以如果你要放第二个物品,那么此时的价值应该是value[1](这里虽然是value[1]但是其实是第二个物品价值) + dp[1][j-weight[1]]对吗?但是此时放了第二个物品就一定比不放的结果dp[1][j]大吗?不一定,所以要做比较,流程图大概就是这样的
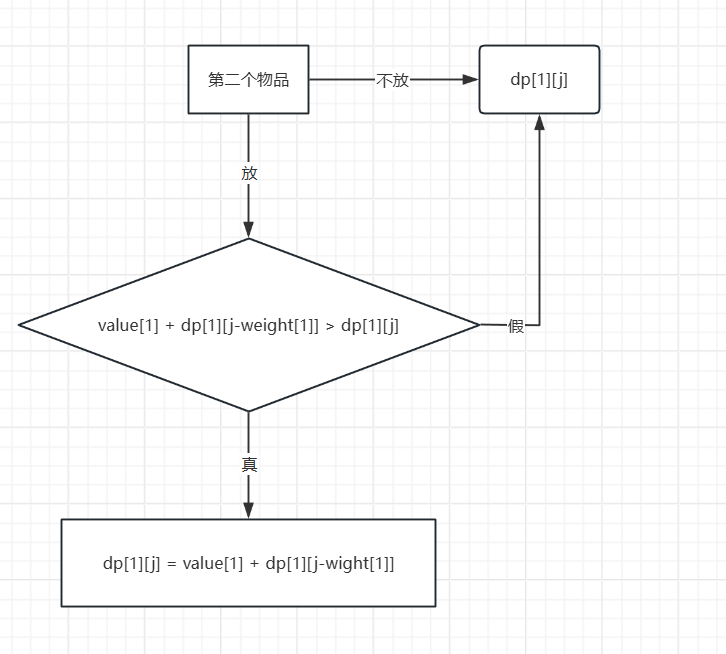
代码如下

这个时候再输出dp[i][j]就可以获取到,考虑i个物品,背包容量为j的时候的最大价值了
完整代码如下:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
/* 01背包问题二维数组 */
int main() {
vector<int> weight = { 1, 3, 4, 5 };
vector<int> value = { 15, 20, 30, 50 };
int wupinNums = weight.size();
int bagMax = 7;
vector<vector<int>> dp(wupinNums + 1, vector<int>(bagMax+1, 0));
// 初始化第一个物品
for (int i = 0; i <= bagMax; i++)
{
if (i >= weight[0])
{
dp[1][i] = value[0];
}
}
// 遍历后面的物品
for (int i = 2; i <= wupinNums; i++)
{
for (int j = 0; j <= bagMax; j++){
if (j >= weight[i-1])
{
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i-1]] + value[i-1]);
}
else
{
dp[i][j] = dp[i - 1][j];
}
}
}
cout << dp[wupinNums][bagMax] << endl;
while (true);
}
为了方便大家理解和测试我把当bagMax=7的时候的所有值都列举出来了
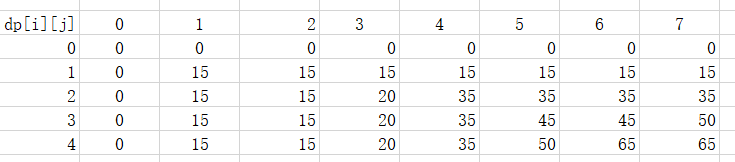




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








