HYSBZ-2660最多的方案-齐肯多夫定理+dp

原创于 2020-07-29 15:45:09 发布 · 648 阅读

1 ·

CC 4.0 BY-SA版权

本文探讨了如何将一个正整数n分解为不同斐波那契数之和的问题，通过齐肯多夫形式分解并使用动态规划方法计算最多可能的组合数。递推式与代码实现详细解析。

最多的方案 HYSBZ - 2660

现在给一个正整数 n，它可以写成一些斐波那契数的和的形式。如果我们要求不同的方案中不能有相同的斐波那契数，那么对一个 n 最多可以写出多少种方案呢？

考虑将数n分解成齐肯多夫形式，然后拆分成段逐位向下分解，显然每一段的贡献是坐标差/2向下取整。因为可能会出现段之间的0影响实际分解情况，所以用dp记录一下每个位置有没有分解。

递推式：
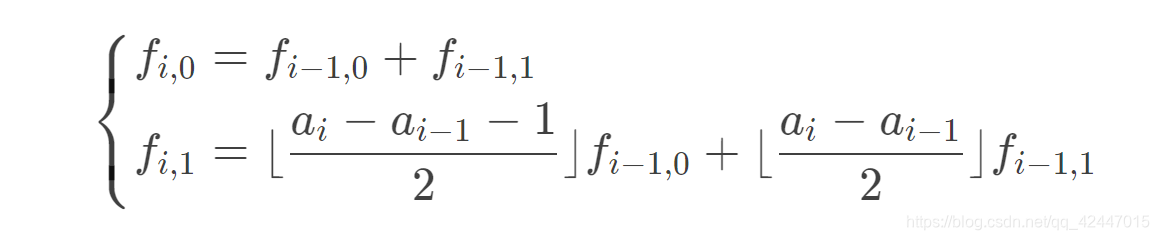
在这里插入图片描述

#include <bits/stdc++.h>

#define ll long long
using namespace std;
const int maxn = 110;
ll f[maxn];
int pos[maxn], g[maxn][2];

int main() {
    ll n;
    cin >> n;
    f[1] = 1, f[2] = 2;
    int m;
    for (m = 3; f[m - 1] <= n; m++)
        f[m] = f[m - 1] + f[m - 2];
//    cout << cnt <<' '<<f[cnt-1];//84 160500643816367088
    --m;
    //齐肯多夫分解
    int cnt = 0;
    for (int i = m; i >= 1; i--)
        if (n >= f[i]) {
            n -= f[i];
            pos[++cnt] = i;
        }
    sort(pos + 1, pos + 1 + cnt);

    //dp
    g[1][1] = 1, g[1][0] = pos[1] - 1 >> 1;
    for (int i = 2; i <= cnt; i++) {
        g[i][1] = g[i - 1][0] + g[i - 1][1];
        g[i][0] = g[i - 1][0] * (pos[i] - pos[i - 1] >> 1) + g[i - 1][1] * (pos[i] - pos[i - 1] - 1 >> 1);
    }
    cout << g[cnt][0] + g[cnt][1];

}