齐次除法（透视除法）的意义

                                          **

齐次除法（透视除法）的意义

我们首先要搞清楚，如何将一个三维坐标点(x, y, z)表示成一个等价的四维齐次坐标
(x, y, z, w)。
根据下列的矩阵变换：

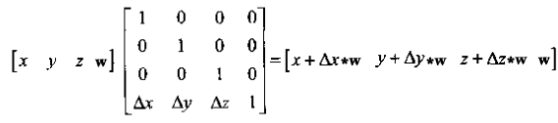
可知，只有当W为1的时候，这个三维坐标转换是等价的，因为这个时候我们才能保证位移的量是正确的，所以（x, y, z, 1）可以等价表示三维的坐标点。如果当W为0时，则没有位移（位移和0相乘得0），所以（x, y, z, 0）可以等价表示三维的向量。因为坐标点和向量井水不犯河水，所以这里也同时排除了坐标点除0的情况。
结论：只有当W=1时，三维坐标点转换成四维齐次坐标点才是等价的，所以一旦发现W不等于1时，就要让W等于1！
<注：此处的概念可以扩展到N维，如二维齐次坐标(x, y, w)中的W的表示，所影响的二维坐标的性质>

那如果W != 1,要如何才能让W=1呢？接下来请看下图。下图中，是一个2D齐次坐标系（即X轴Y轴W轴所构成的三维空间），假设有一平面平行于X和Y轴，且W坐标为1，我们暂且把这个平面叫做W=1平面。在W=1平面上有一点（x,y），二