徒手挖地球十二周目

徒手挖地球十二周目

NO.36 有效数独 中等

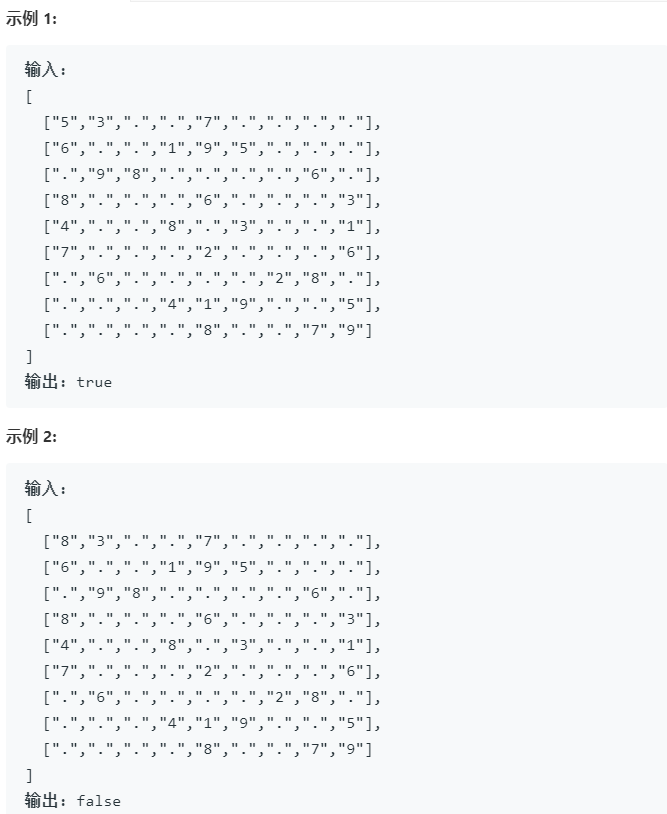
思路一：暴力法 依次遍历完每一行，每一列，每一个一个子数独。

public boolean isValidSudoku(char[][] board) {
        if (board==null||board.length<9)return false;
        Set<Character> set=new HashSet<>();
        //遍历每一行判断是否有重复
        for (int i=0;i<9;i++){
            //遍历完一行之后清空set
            set.clear();
            for (int j=0;j<9;j++){
                //如果这个元素是1-9，则判断是否重复元素
                if (board[i][j]>='1'&&board[i][j]<='9'){
                    if (set.contains(board[i][j])){
                        return false;
                    }else {
                        set.add(board[i][j]);
                    }
                }
            }
        }
        //遍历每一列判断是否有重复元素
        for (int j=0;j<9;j++){
            set.clear();
            for (int i=0;i<9;i++){
                if (board[i][j]>='1'&&board[i][j]<='9'){
                    if (set.contains(board[i][j])){
                        return false;
                    }else {
                        set.add(board[i][j]);
                    }
                }
            }
        }
        //遍历每一个3*3矩阵是否有重复元素
        for (int k=0;k<3;k++){
            for (int m=0;m<3;m++){
                set.clear();
                for (int i=0;i<3;i++){
                    for (int j=0;j<3;j++){
                        if (board[i+(3*m)][j+(3*k)]>='1'&&board[i+(3*m)][j+(3*k)]<='9'){
                            if (set.contains(board[i+(3*m)][j+(3*k)])){
                                return false;
                            }else {
                                set.add(board[i+(3*m)][j+(3*k)]);
                            }
                        }
                    }
                }
            }
        }
        return true;
    }

时间复杂度：对所有元素进行三次遍历，O(3n)，在这个题目的约束下(都是9*9的数独)，对81个元素三次遍历，时间复杂度可以看做常数次，即O(1)。

思路二：优化暴力法，一次遍历 空间换时间，定义27个数组(9行+9列+9个子数独)。只需要遍历一次，将每个元素与其对应的行数组、列数组、子数独数组中判断是否出现重复即可。

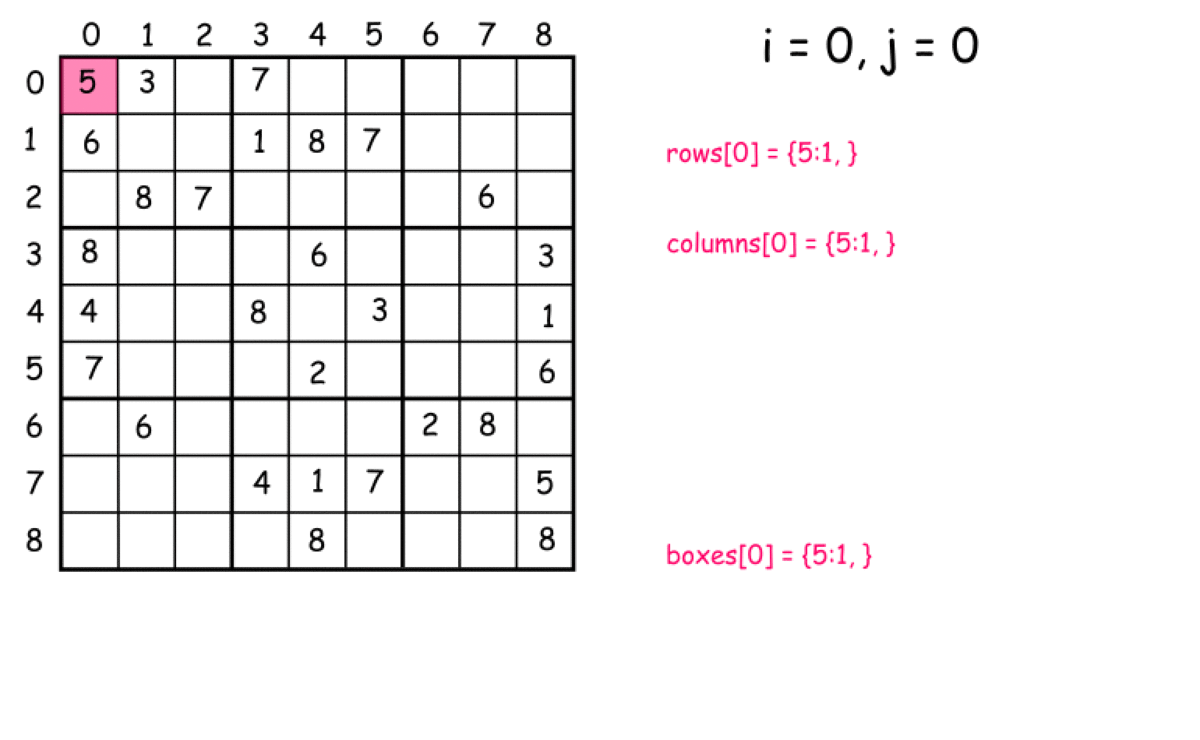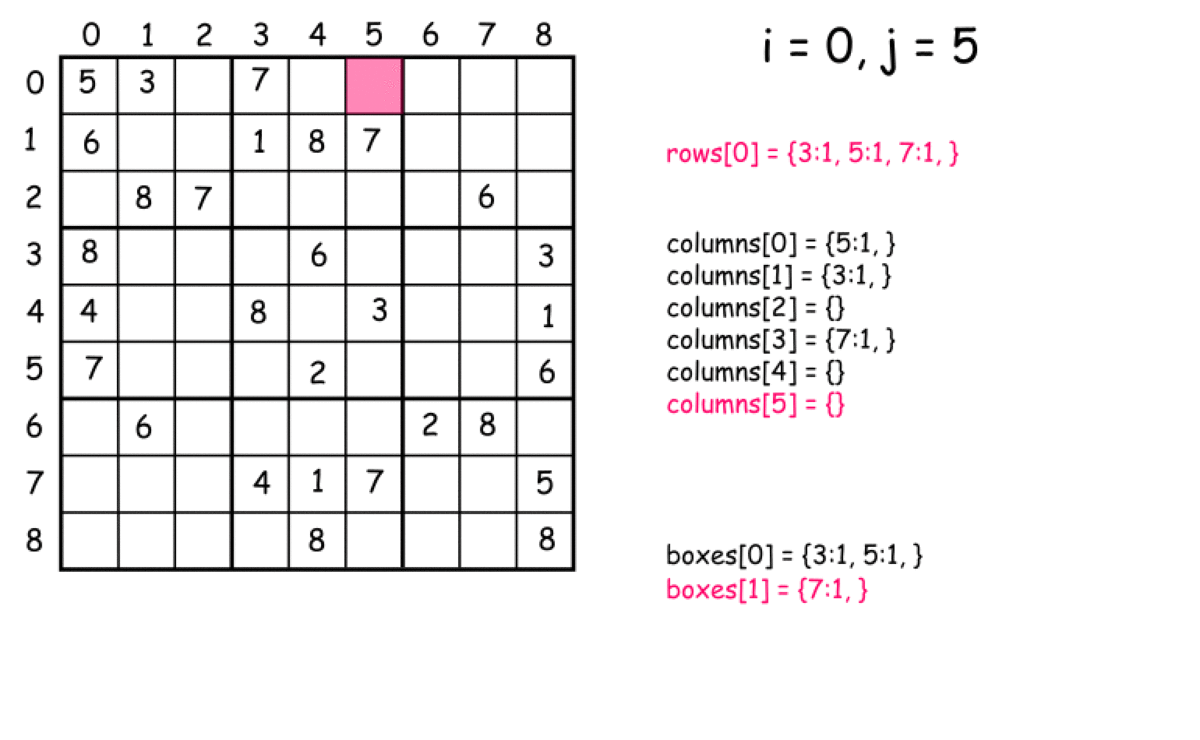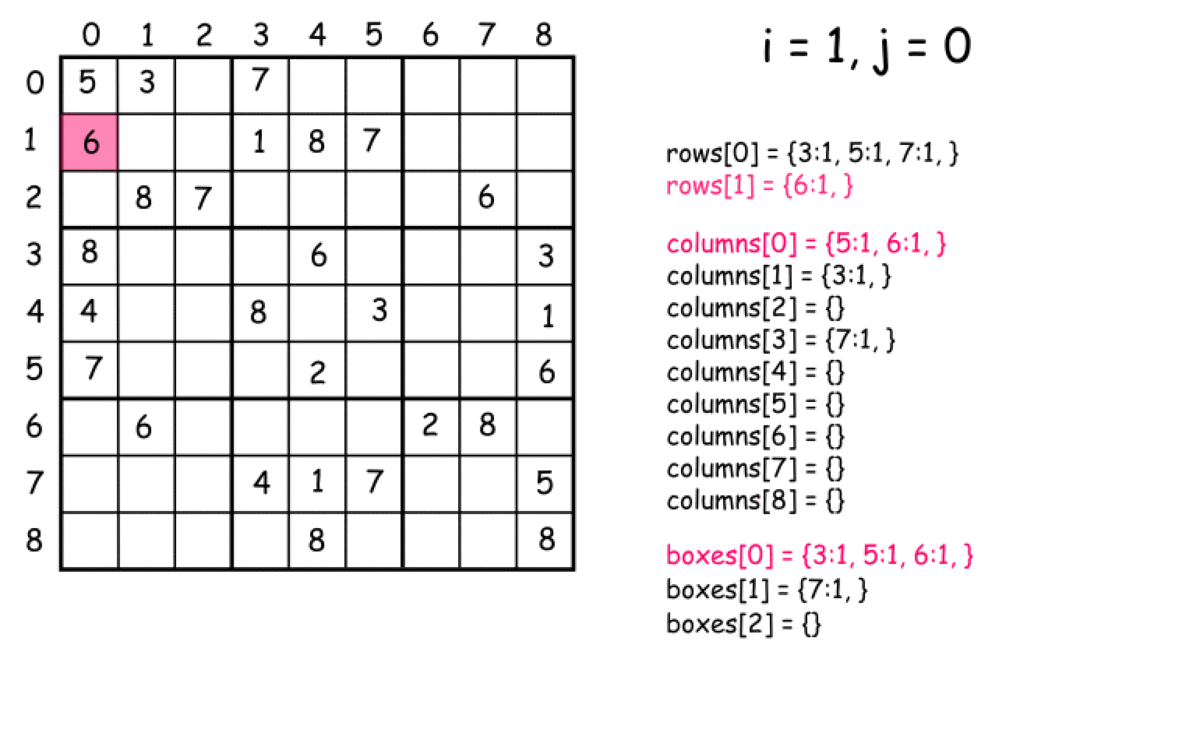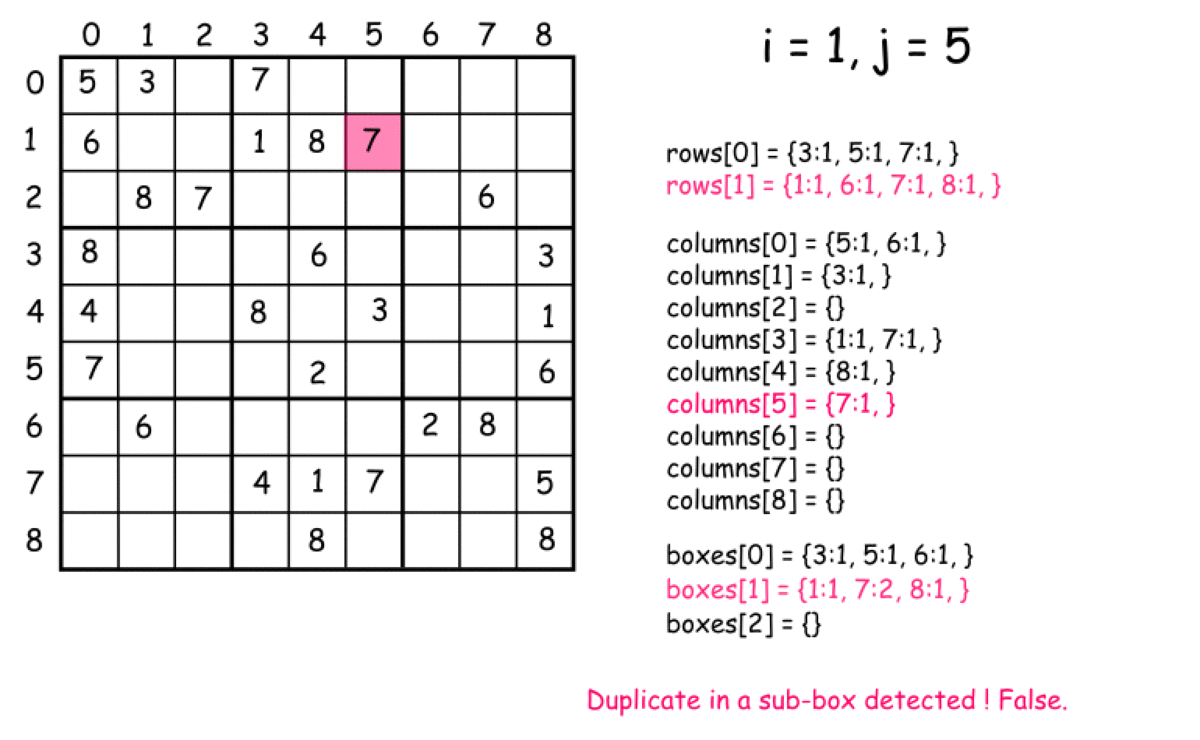
判断元素所属的行和列是很容易的，如何判断每个元素属于第几个子数独需要思考：box_index=(i/3)*3+j/3

public boolean isValidSudoku(char[][] board) {
        //用三个二维数组分别分别记录9行、9列、9个子数独中的元素，用来判断是否重复
        int[][] rows=new int[9][9];
        int[][] cols=new int[9][9];
        int[][] boxes=new int[9][9];
        //遍历数独中每个元素
        for (int i=0;i<9;i++){
            for (int j=0;j<9;j++){
                char c = board[i][j];
                //如果被遍历元素是数字，则添加到其对应的数组中进行记录
                if (c>='1'&&c<='9'){
                    int box_index=(i/3)*3+j/3;
                    rows[i][c-'0'-1]++;
                    cols[j][c-'0'-1]++;
                    boxes[box_index][c-'0'-1]++;
                    //判断是否出现重复
                    if (rows[i][c-'0'-1]>1||cols[j][c-'0'-1]>1||boxes[box_index][c-'0'-1]>1)return false;
                }
            }
        }
        return true;
    }

时间复杂度：数独中9*9个元素遍历一次，O(n)，但是在这个题目的约束下(都是9*9的数独)，对81个元素一次遍历，时间复杂度可以看做常数次，即O(1)。

思路三：一次遍历，移位编码，位图法 思路二相对于思路一虽然只需要一次遍历，但是空间上付出的“代价”让人不爽，可以借助位图进行优化。这里就不赘述各种算术运算符的作用了，有需要的请百度，都比我说得好。

很容易发现，导致空间浪费的原因是我们申请了int(32位)类型的数组，但是每个元素最大只需要表示到2，也就是每个元素数值部分实际上只需要2位即可。那么我们很容易想到：申请byte(8位)类型就好了。这确实是一种方法，但是我们使用位图这种数据结构来完成，节省空间的同时，还可以使算法的速度得到优化。

我们需要申请一个int类型的数组map，但是我们将每个32位元素的前0-8位分别表示同一数字出现在第几行中，9-17位分别表示同一数字出现在第几列中，18-26位分别表示数字出现在第几个子数独中，对应位上0表示该数字未出现过，1表示该数字出现过。上述情况可以使用左移运算来实现，还需要使用按位与运算实现判断某行、某列、某子数独是否存在重复情况，使用按位或运算将数字加入对应的数组元素。

public boolean isValidSudoku(char[][] board) {
    int[] map=new int[9];
    for (int row=0;row<9;row++){
        for (int col=0;col<9;col++){
            char c = board[row][col];
            if (c!='.'){
                //0-8位表示行号，9-17位表示列号，18-26位表示第几个子数独
                int index=1<<(0+row)|1<<(9+col)|1<<(18+row/3*3+col/3);
                //按位与等于0说明该数字不曾在同一行、列、子数独中出现过
                if ((map[c-'0'-1]&index)==0){
                    //按位或将数字加入数组对应元素
                    map[c-'0'-1]|=index;
                }else {
                    return false;
                }
            }
        }
    }
    return true;
}

时间复杂度：数独中9*9个元素遍历一次，O(n)，但是在这个题目的约束下(都是9*9的数独)，对81个元素一次遍历，时间复杂度可以看做常数次，即O(1)。

NO.38 外观数列 简单

这道题读题花了我好一会儿，最后还是在别人的帮助下理解题意。。。这个外观数列的意思是：第一项 “1”；第二项描述第一项：1个1，“11”；第三项描述第二项：2个1，“21”；第四项描述第三项：1个2和1个1，“1211”；第五项描述第四项：1个1和1个2和2个1，“111221”。。。。

思路一：按序生成每个数列 按顺序依次生成每个“外观数列”，其实就是BF。

public String countAndSay(int n) {
    //第一项外观数列为"1"
    if (n==1)return "1";
    String s="1";
    //按序生成n个外观数列，从第二项开始
    for (int i=0;i<n-1;i++){
        //temp是当前生成的外观数列、c初始化为前一项的第一个字符、count记录前一项连续相等的的字符
        StringBuilder temp=new StringBuilder();
        char c = s.charAt(0);
        int count=1;
        //遍历前一项外观数列的每个字符
        for (int j=1;j<s.length();j++){
            //如果连续的字符相等，则count计数器增加
            if (c==s.charAt(j)){
                count++;
            }else {
                //如果连续字符不相等，则将连续字符数量和字符拼接至temp
                temp.append(count).append(c);
                //c更新为当前遍历的字符，计数器重置为1
                c=s.charAt(j);
                count=1;
            }
        }
        //注意，很容易遗漏的一步：将最后未拼接的字符加入temp
        temp.append(count).append(c);
        //更新s
        s=temp.toString();
    }
    return s;
}

时间复杂度不会算。。。

NO.39 组合总数 中等

思路一：深度遍历，回溯法 深度遍历得到”全排列“的过程中回溯剪枝。目标值作为根节点，每个分做减法，如果目标值被减为0则结算此分支路径上的减数集合，如果目标值被减为负数则剪枝即可。

去重：每个分支节点上的减数的下标不能比本分支上一层节点的减数的下标小。即，上层节点的减数下标为3，则同分支下一层节点的减数下标要从3开始。(这样每个分支就不会重复使用之前使用过的元素)

List<List<Integer>> res=new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
    if (candidates==null)return res;
    dfs(target,0,new Stack<Integer>(),candidates);
    return res;
}
//深度遍历
private void dfs(int target, int index, Stack<Integer> pre, int[] candidates) {
    //等于零说明结果符合要求
    if (target==0){
        res.add(new ArrayList<>(pre));
        return;
    }
    //遍历，index为本分支上一节点的减数的下标
    for (int i=index;i<candidates.length;i++){
        //如果减数大于目标值，则差为负数，不符合结果
        if (candidates[i]<=target){
            pre.push(candidates[i]);
            //目标值减去元素值
            dfs(target-candidates[i],i,pre, candidates);
            //每次回溯将最后一次加入的元素删除
            pre.pop();
        }
    }
}