天勤2022数据结构（六）图

最新推荐文章于 2023-07-04 14:47:07 发布
最新推荐文章于 2023-07-04 14:47:07 发布
阅读量933 收藏 13
点赞数
分类专栏： 考研 数据结构 文章标签： 数据结构 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_43130927/article/details/115975113
版权

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

天勤2022数据结构（六）图

前言

邻接矩阵

typedef struct{
	int no;	顶点编号
	char info;
}VertexType; 

typedef struct{
	int edges[maxSize][maxSize];
	int n, e;	顶点数，边数
	VertexType[maxSize];
}MGraph;

邻接表

typedef struct ArcNode{
	int adjvex;	边指向的结点
	struct ArcNode *nextarc;
	int info;
}ArcNode; 

typedef struct{
	char data;
	ArcNode *firstarc;
}VNode;

typedef struct{
	VNode adjlist[maxSize];
	int n, e;
}AGraph;

强连通图：

当且仅当G中有一个回路，它至少包含每个节点一次

一、基础算法

存储结构：邻接表

  1. DFS（类似树先序

    int visit[maxSize];
void DFS(AGraph *G, int v){
	ArcNode *p;
	visit[v] = 1;
	Visit(v);
	p = G->adjlist[v].firstarc;
	while(p!=NULL){
		if(visit[p->adjvex] == 0){
			DFS(G, p->adjvex);
		}
		p = p->nextarc;
	}
}

void dfs(AGraph *g){
	for(int i = 0; i<g->n; i++){
		if(visit[i] == 0){
			DFS(g, i);
		}
	}
}

  2. BFS（类似树层次

    void BFS(AGraph *G, int v, int visit[maxSize]){
	ArcNode *p;
	int que[maxSize], front = 0, rear = 0;
	int j;
	Visit(v);
	visit[v] = 1;
	rear = (rear + 1) % maxSize;
	que[rear] = v;
	while(front != rear){
		front = (front + 1) % maxSize;
		j = que[front];
		p = G->adjlist[j].firstarc;
		while(p != NULL){
			if(visit[p->adjvex] == 0){
				Visit(p->adjvex);
				visit[p->adjvex] = 1; 
				rear = (rear + 1) % maxSize;
				que[rear] = p->adjvex;
			}
			p = p->nextarc;
		}
	}
}

void bfs(AGraph *g){
	for(int i = 0; i<g->n; i++){
		if(visit[i] == 0){
			BFS(g, i, visit);
		}
	}
}

    例题

    1. 求不带权无向连通图G中距离顶点最远的一个顶点

      返回广搜最后一个结点

      int BFS(AGraph *G, int v){
	ArcNode *p;
	int que[maxSize], front = 0, rear = 0;
	int visit[maxSize];
	int i, j;
	for(i = 0; i<G->n; i++){
		visit[i] = 0;
	}
	rear = (rear + 1) % maxSize;
	que[rear] = v;
	visit[v] = 1;
	while(front != rear){
		front = (front + 1) % maxSize;
		j = que[front];
		p = G->adjlist[j].firstarc;
		while(p != NULL){
			if(p -> adjvex == 0){
				visit[p->adjvex] == 1;
				rear = (rear + 1) % maxSize;
				que[rear] = p->adjvex;
			}
			p = p->nextarc;
		}
	}
	return j;
}

    2. 判断无向图G是否是一棵树。若是树，返回1，否则返回0

      无向图是树：①n-1条边 ②n个顶点 ③连通图

      void DFS(AGrapg *G, int v, int &vn, int &en){
	ArcNode *p;
	visit[v] = 1;
	++vn; vn顶点计数器
	p = G->adjlist[v].firstarc;
	while(p != NULL){
		++en；边计数器
		if(visit[p->adjvex] == 0){
			DFS(G, p->adjvex, vn, en);
		} 
		p = p->nextarc;
	}
}

int GisTree(AGraph *G){
	int vn = 0, en = 0, i;
	for(i = 0; i<G->n; ++i){
		visit[i] = 0;
	}
	DFS(G, 1, vn, en);
	if(vn == G->n && (G->n-1) == en/2)
		return 1;
	return 0;
}

    3. 邻接表判断顶点 i i i和顶点 j j j（ i ! = j i!=j i!=j）之间是否有路径

      i i i开始深搜，遇到 j j j则有

      int dfs(AGraph *G, int i, int j){
	int k;
	for(k = 0; k<G->n; k++){
		visit[k] = 0;
	}
	DFS(G, i);
	if(visit[j] == 1)
		return 1;
	return 0;
}

Prim算法

v s e t [ i ] vset[i] vset[i] 顶点是否生成树中
l o w c o s t [ i ] lowcost[i] lowcost[i] 当前生成树到剩余各顶点最短边的权值

void Prim(MGraph g, int v0, int &sum){
	int lowcost[maxSize], vset[maxSize], v;
	int i, j, k, min;
	v = v0;
	for(int i = 0; i<g.n; i++){
		vset[i] = 0;
		lowcost[i] = g.edges[v0][i];
	}
	vset[v0] = 1;
	sum = 0;
	for(i = 0; i<g.n-1; i++){
		//找相邻最小边
		min = INF;
		for(j = 0; j<g.n; j++){
			if(vset[j] == 0 && lowcost[j] < min){
				min = lowcost[j];
				k = j;
			}
		}
		v = k;
		vset[k] = 1;
		sum += min;
		// 更新/维护
		for(j = 0; j<g.n; j++){
			if(vset[j] == 0 && g.edges[v][j] < lowcost[j]){
				lowcost[j] = g.edges[v][j];
			}
		} 
	}
}

Kruskal算法

typedef struct{
	int a, b;
	int w;
}Road;

Road road[maxSize];
int v[maxSize];

int getRoot(int a){
	while(a != v[a])
		a = v[a];
	return a;
}

void Kruskal(MGraph g, int &sum, Road road[]){
	int i;
	int N, E, a, b;
	N = g.n;E = g.e;sum = 0;
	for(i = 0; i<N; i++){
		v[i] = i;
	}
	sort(road, E);
	for(i = 0; i<E; i++){
		a = getRoot(road[i].a);
		b = getRoot(road[i].b);
		if(a != b){
			v[a] = b;
			sum += road[i].w;
		}
	}
}

Dijkstra算法

d i s t [ v i ] dist[v_i] dist[vi​]     当前已找到的从v0到每个终点vi的最短路径总长度
p a t h [ v i ] path[v_i] path[vi​]    从v0到vi最短路径上vi的前一个顶点
s e t [ v i ] set[v_i] set[vi​]       标记数组

void Dijkstra(MGraph g, int v, int dist[], int path[]){
	int set[maxSize];
	int min, i, j, u;
	// Initialize
	for(i = 0; i<g.n; i++){
		dist[i] = g.edges[v][i];
		set[i] = 0;
		if(g.edges[v][i] < INF)
			path[i] = v;
		else
			path[i] = -1;
	}
	set[v] = 1;
	path[v] = -1;
	// Find shortest path
	for(i = 0; i<g.n-1; i++){
		min = INF;
		// Find a node which dist is shortest
		for(j = 0; j<g.n; j++){
			if(set[j] == 0 && dist[j] < min){
				u= j;
				min = dist[j];
			}
		}
		set[u] = 1;
		// Update dist[] and path[]
		for(j = 0; j<g.n; j++){
			if(set[j] == 0 && dist[u] + g.edges[u][j] < dist[j]){
				dist[j] = dist[u] + g.edges[u][j];
				path[j] = u;
			}
		}
	}
}

Floyd算法

d i s t [ v i ] dist[v_i] dist[vi​]     当前已找到的任意两顶点的最短路径长度
p a t h [ v i ] path[v_i] path[vi​]    从v0到vi最短路径上vi的前一个顶点

void Floyd(MGraph *g, int path[][maxSize], int dist[][maxSize]){
	int i, j, k;I
	// Initialize
	for(i = 0; i<g->n; i++){
		for(j = 0; j<g->n; j++){
			dist[i][j] = g->edges[i][j];
			path[i][j] = -1;
		}
	}
	// Find and update
	for(k = 0; k<g->n; k++){
		for(i = 0; i<g->n; i++){
			for(j = 0; j<g->n; j++){
				if(dist[i][k] + dist[k][j]<dist[i][j]){
					dist[i][j] = dist[i][k] + dist[k][j];
					path[i][j] = k;
				}
			}
		}
	}
}

void printPath(int u, int v, int path[][maxSize], int dist[][maxSize]){
	if(dist[u][v] == INF)
		return;
	else{
		if(path[u][v] == -1){
			printf("<%d,%d>", u, v);
		}else{
			int mid = path[u][v];
			printPath(u, mid, path, dist);
			printPath(mid, v, path, dist);
		}
	}
}

拓扑排序

typedef struct{
	int data;
	int count;
	ArcNode* first;
}VNode;

int TopSort(AGraph *G){
	int i, j, n = 0;
	int stack[maxSize], top = -1;
	ArcNode *p;
	// Initialize
	for(i = 0; i<G->n; i++){
		if(G->adjList[i].count == 0){
			top++;
			stack[top] = i;
		}
	}
	// Find
	while(top != -1){
		i = stack[top];
		top--;
		n++;
		cout<<i<<" ";
		
		p = G->adjList[i].first;
		while(p != NULL){
			j = p->adjV;
			(G->adjList[j].count)--;
			if(G->adjList[j].count == 0){
				top++;
				stack[top] = j;
			}
			p = p->next;
		}
	}
}

二、综合应用题

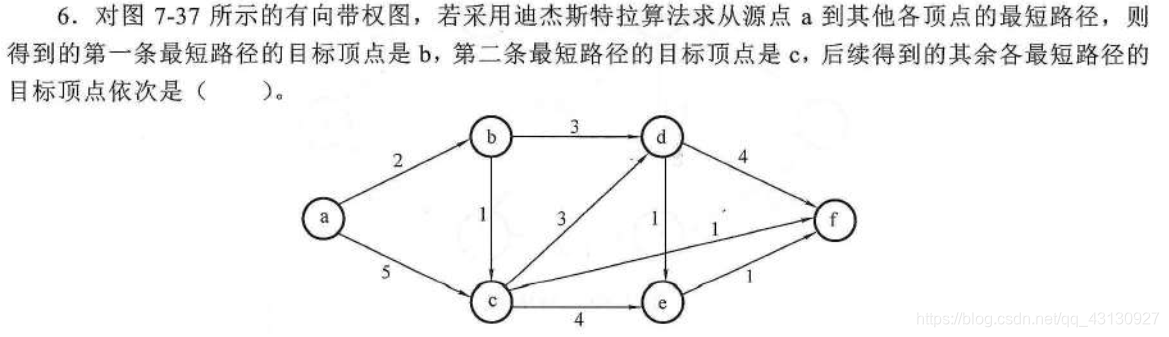
  • 附加在这里插入图片描述

    已并入的顶点dist[a], pre[a]dist[b] , pre[b]dist[c], pre[c]dist[d], pre[d]dist[e], pre[e]dist[f], pre[f]
    a-2,-5,----
    a, b3,b5,b
    a, b, c5,b9,c6,c
    a, b, c, d9,c6,c
    a, b, c, d, f9,c
    a, b, c, d, f, e
    • 用邻接矩阵表示图时，矩阵元素的个数与顶点个数是否有关？与边的条数是否有关？

    与顶点个数有关 边的条数无关

  2. 请回答关于图的下列问题:

    1. 有n个顶点的有向强连通图最多有多少条边？最少有多少条边？

      最多： 两两相连    n(n-1)
      最少： 围成一圈    n

    2. 对于一个有向图，不用拓扑排序，实现判断图中是否存在经过给定顶点v0的环的算法

      思路：
      深搜邻接表，回溯（因为下次寻找路径，路径中的结点可能重复遇到，因此要还原现场）

      bool DFS(AGraph *G, int v, bool visited[]){
	bool flag;
	ArcNode *p;
	visited[v] = true;
	for(p = G->adjList[v].first; p!=NULL; p = p->next){
		if(vistied[p->adjV] == true)
			return true；
		else
			flag = DFS(G, p->adjV, visited);
		
		if(flag == true)
			return true;
		visited[p->adjV] = 0;
	}
	return false;
}

  3. 设G＝（V，E）以邻接表存储，如图所示，试画出图的深度优先和广度优先生成树
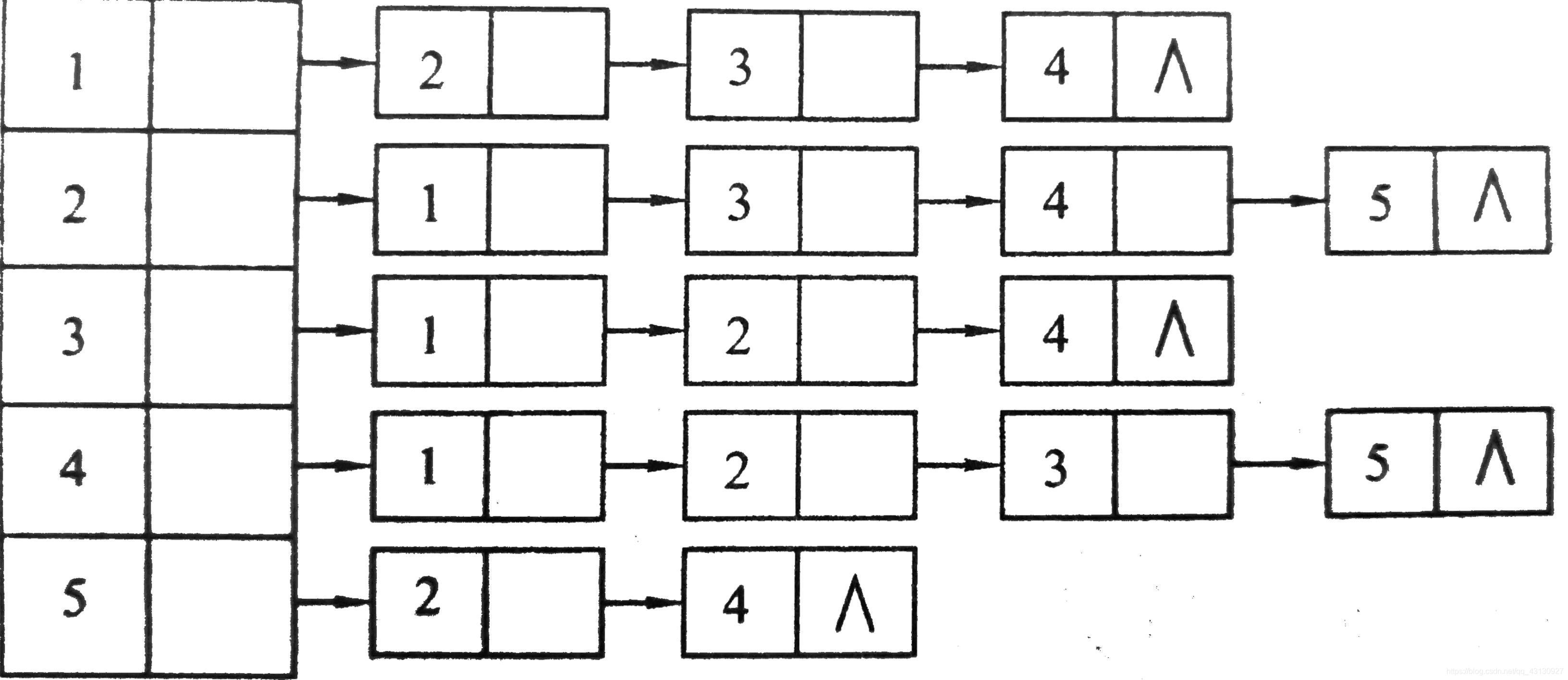
    在这里插入图片描述

    1. 写出遍历序列：
      深度优先遍历序列：
      <1,2> <2,3> < 3,4> <4,5>
      广度优先遍历序列
      <1,2> <1,3> <1,4> <2,5>
    2. 由边的序列画出搜索生成树
      深度优先生成树：
      深度优先生成树
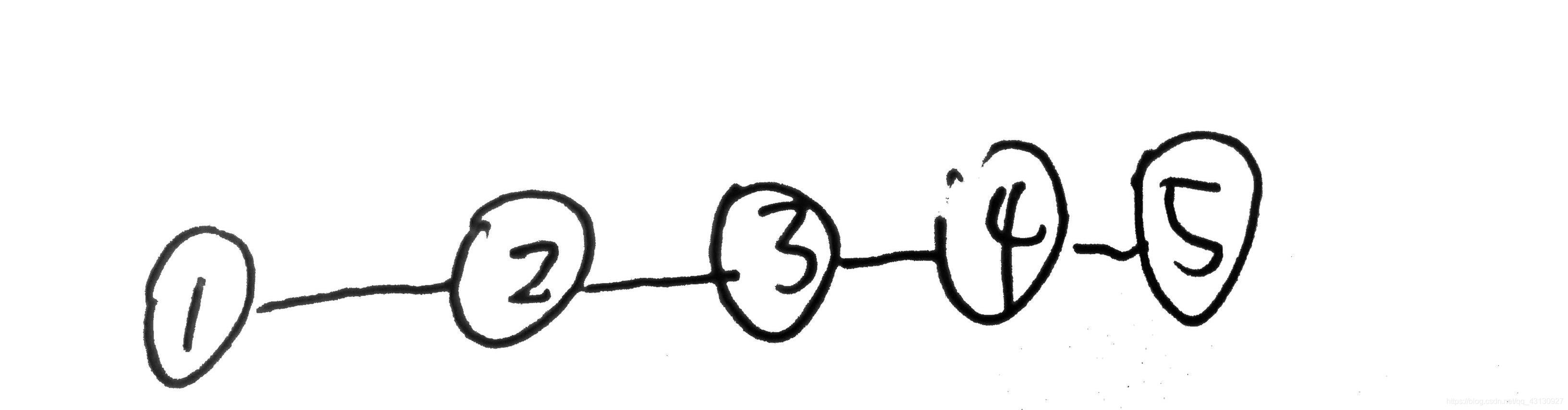
      广度优先生成树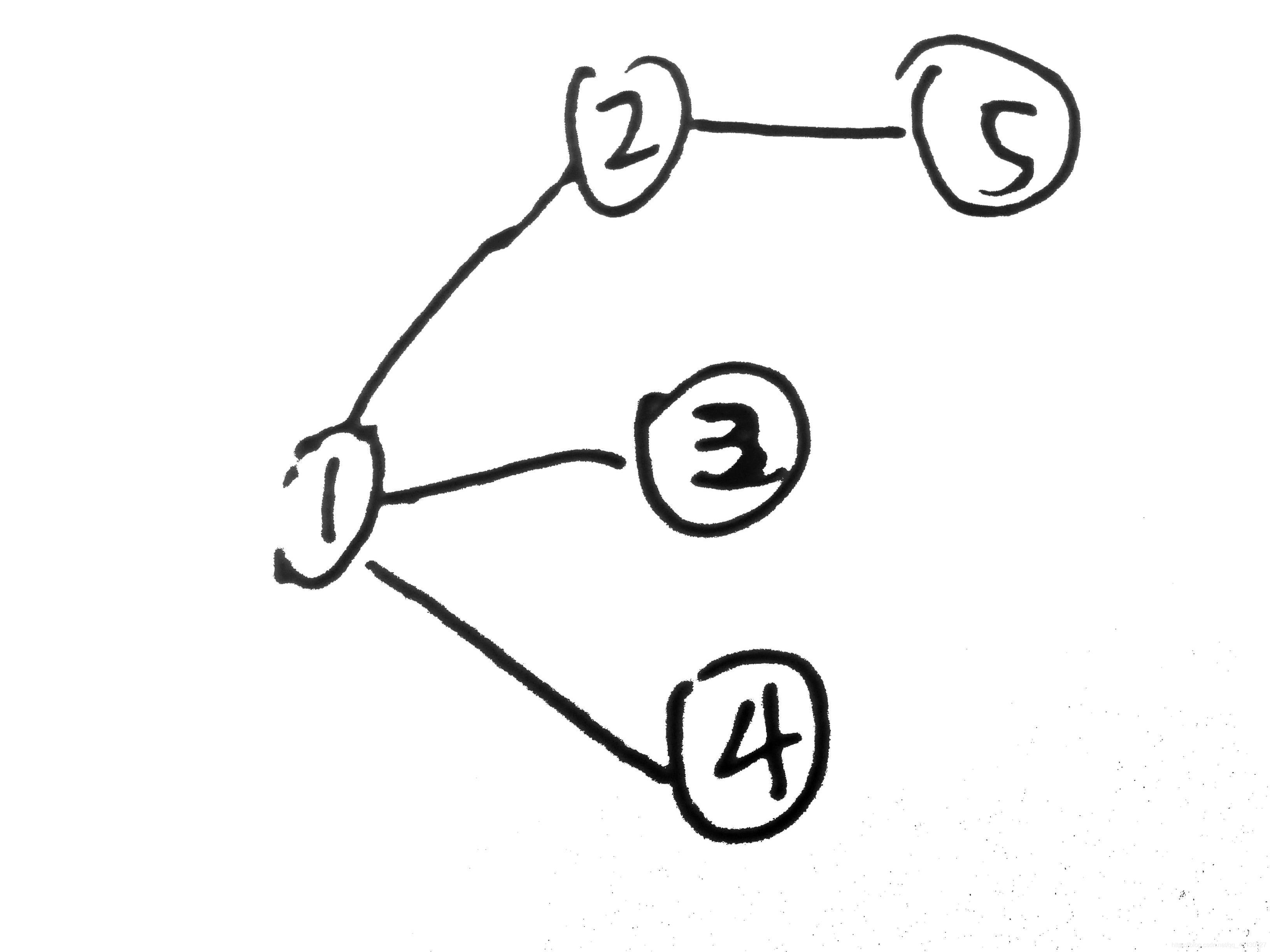：广度优先生成树

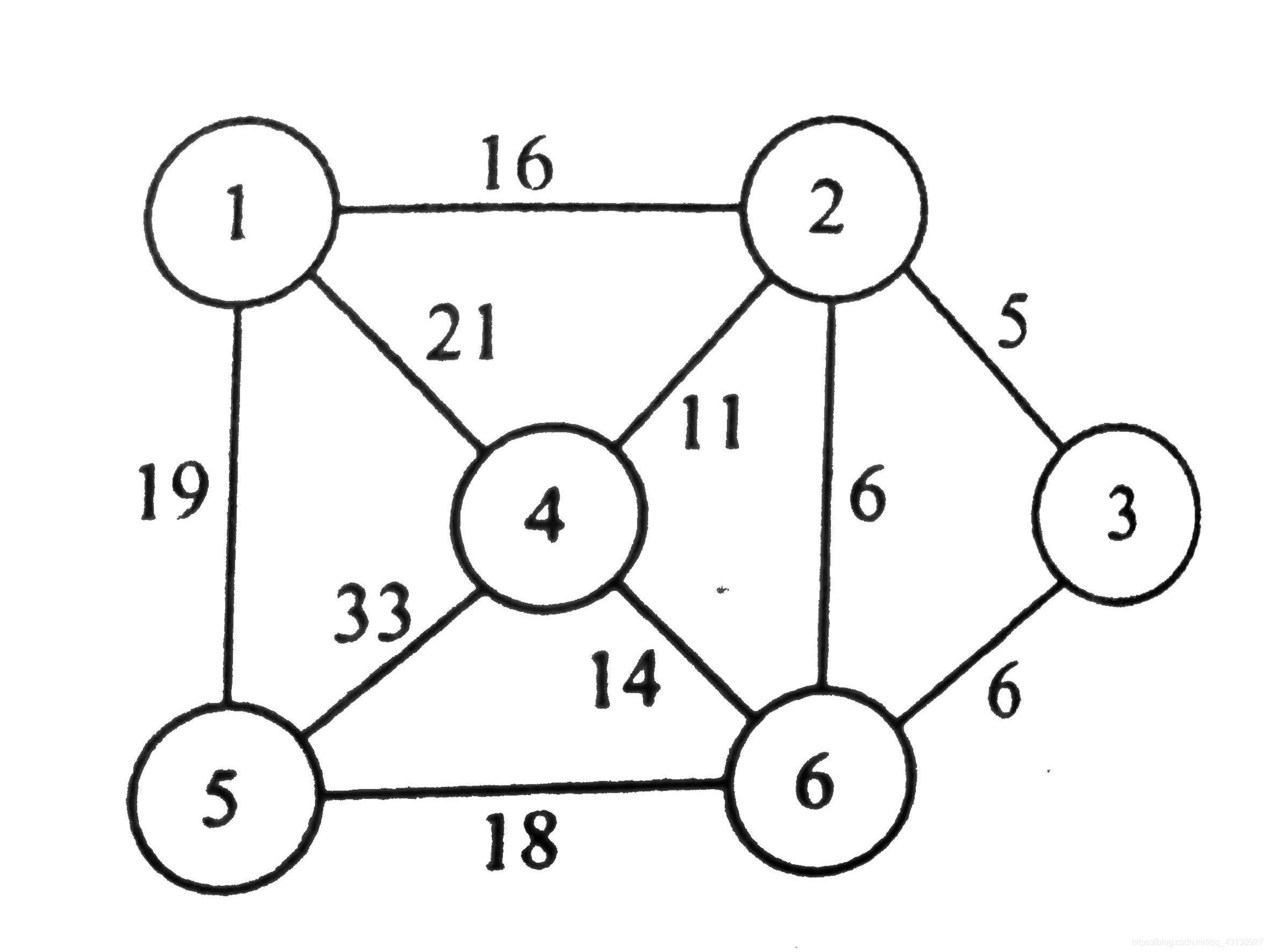
  4. 如图所示为一个地区的通信网，边表示城市间的通信线路，边上的权表示架设线路花费的代价，如何选择能沟通每个城市且总代价最省的n-1条线路，画出所有可能的选择。在这里插入图片描述

总结

提示：这里对文章进行总结：

HDU-Dade
关注
  • 0
    点赞
  • 踩
  • 13
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
数据结构的知识梳理图.zip
03-27
该思维导图结合wang_dao tian_qin以及个人平时做的题，凝练而成，值得初学计算机的朋友使用。 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
五分钟学编程：如何学好数据结构与算法？
weixin_72959097的博客
07-17 108
简介学习编程，数据结构是你必须要掌握的基础知识，那么数据结构到底是什么呢？根据百度百科的介绍，数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下，精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。听听这是人话么，我帮你们翻译一下，其实数据结构就是用来描述计算机里存储数据的一种数学模型，因为计算机里要存储很多乱七八糟的数据，所以也需要不同的数据结构来描述。本文思维导图为什么要学数据结构。
算法数据结构 思维导图学习系列（1）- 数据结构 8种数据结构 数组（Array）链表（Linked List）队列（Queue）栈（Stack）树（Tree）散列表（Hash）堆（Heap）图
sinat_22510827的博客
10-22 240
算法数据结构 思维导图学习系列（1）- 数据结构 8种数据结构 数组（Array）链表（Linked List） 队列（Queue） 栈（Stack） 树（Tree）散列表（Hash） 堆（Heap） 图（Graph） 树的高度和深度 深度定义是从上往下的，高度定义是从下往上的。（其实不用在意这个，反正树的深度高度怎么数都一样的）。 深度和高度涉及到结点的层数，有的教材规定根结点在第0层，有的则规定根结点在第1层。原理都是一样的，因教材而异。树从根结点开始往下数，叶子结点所在的最大层数称为 树.
算法最后一次作业
m0_53555511的博客
10-21 125
//邻接矩阵和邻接表的dfs算法 #include <iostream> #include <stdio.h> using namespace std; #define INF 1000000 #define MAXL 100 #define MAXV 100 //图的邻接矩阵类型的声明 typedef struct{ int no;//顶点编号 char data[MAXL];//顶点其他信息 }VertexType; typedef struct{ int edges[.
考研天勤 数据结构 图（自用回顾）
qq_52483547的博客
10-10 1020
数据结构-图的相关算法
2024数据结构考研笔记（王道精讲课+天勤高分笔记）
weixin_51252109的博客
07-04 3870
(https://cdn.jsdelivr.net/gh/Tarench/image@master/20230316130938.png)]插入删除查找。
【天勤|数据结构】二叉树
ljc2330419164的博客
04-10 104
对于一般的树加两个限制条件每个结点最多只有两个子树字数有左右之分，不能颠倒。
无向图的最短路径代码（prim, kruskal）
Hu_Linson的博客
12-19 679
以下代码来自天勤数据结构 Prim //prim算法是每次寻找当前树距离其他顶点最短的边（不构成回路） void Prim(Mgraph g,int v0,int &sum) { int lowcost[maxsize],vset[maxsize],v; int i,j,k,min; v=v0; for(i=0;i<g.n;i++) { lowcost[i]=g.edges[v0][i]; vset[i]=0; } vset[v0]=1;//将v0并入数中 s
天勤数据结构——绪论
xun08042的博客
07-19 747
数据类型 结构型 结构体 指针型 int *a；//指向字符型变量的指针a，这里只是定义一个变量名，还没指向地址 如果a是个指针型变量，且它已经指向了一个变量b，则a中存放变量 b所在的地址。*a就是取变量b的内容（x=*a;等价于x=b;)，&b就是取变量b的地址，语句 a=&b;就是将变量b的地址存于a中，即大家常说的指针a指向b。 结点的构造 链表结点 typedef struct Node { int data ; //这里默认的是int型，如需其他类型可修改 struc
数据结构思维导图，超全！超详细！
热门推荐
SuperOnly2222的博客
04-17 1万+
文章目录数据结构思维导图一、数据结构基本概念二、线性表三、栈和队列四、树五、图六、查找七、排序八、二叉树与树与森林 数据结构思维导图 我在一个平台（忘记了）上发现了一个博主制作的数据结构思维导图，感觉很好就下载了下来，但原图太大，没有办法上传，我就一章节一章节的截成了8张图，希望对你有帮助。 一、数据结构基本概念 二、线性表 三、栈和队列 四、树 五、图 六、查找 七、排序 八、二叉树与树与森林 ...
2019天勤数据结构高分笔记
08-29
分享给时间不够又急于找资源的同学们，实在木有积分的可以私信。
2019天勤数据结构
09-05
简单易懂的数据结构PDF，适合零基础理解晦涩难懂的数据 结构
天勤数据结构
08-15
解压后,包含两个PDF文件,天勤数据结构近两年的版本(2018版/2019版),资源不用介绍,你们都有备而来,一起学习吧
天勤数据结构视频资料学习.zip
09-14
考研天勤视频课，天勤相对王道来说易懂一些，比较通俗易懂
天勤2019数据结构无水印可打印
12-11
天勤2019数据结构计算机考研复习指导电子版PDF 天勤2019计算机组成原理计算机考研复习指导无水印版. 天勤2019年计算机网络(高清版)
天勤2019数据结构
11-17
天勤2019数据结构，pdf版本，推荐新手学习，非常适合考研到计算机专业的学生，有利于广大学生的编程思想的形成。
2020 天勤数据结构 高分笔记 + 习题
03-31
数据结构 考研 官方用书 pdf高清版，另有习题。
天勤2022数据结构（一）线性表
Zheng_LH
03-16 2338
天勤2022数据结构（一）线性表前言一、基础题二、使用步骤1.引入库2.读入数据总结 前言 提示：全文为作者手打，仅供个人复习使用 一、基础题 线性表可用顺序表和链表存储，试问： 如果有n个表同时并存，并且在处理过程中各表的长度会动态发生变化，表的总数也可能自动改变，在此情况下，应选用哪种存储表示？为什么？ 用链表。如果采用顺序表，在多个表并存的情况下，一旦发现某个表有存满并溢出的情况，很可能 若表的总数基本稳定，且很少进行插入和删除但要求以最快的速度存取表中的元素，这时用哪种存储表示？为
【计算机复试】计算机网络模块复习
Zheng_LH
03-06 1089
研究生复试巩固TCP/IP 位于哪一层UDP有哪些应用计算机网络中有哪些流量控制，缓存满了怎么调度子网掩码的作用交换机、路由器和集线器的区别 自己给自己出题目 TCP/IP 位于哪一层 TCP/IP 有几层，为什么没有物理层 四层，应用层、TCP/UDP、IP、网络接口层 因为数据链路层和物理层合并为网络接口层 TCP和UDP有什么区别 UDP：无连接，尽最大可能交付，没有拥塞控制，面向报文，支持一对一、一对多、多对多，首部只有8个字节 TCP：面向连接，提供可靠交付，有流量控制，拥塞
天勤数据结构2024版
最新发布
10-12
关于天勤数据结构2024版，我不太清楚具体情况，但是我可以告诉你一些关于数据结构的基础知识。 数据结构是计算机科学中的一个重要概念，它是指数据对象在计算机中的组织方式。常见的数据结构包括数组、链表、栈、...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值