【C基础】15 位运算和位域

一、移位运算

运算符	含义
<<	左移
>>	右移

1.1 << 左移

• i << j
  • 将 i 中的所有位向左移动 j 个位置，右边补 0；
  • 所有小于 int 的类型，移位以 int 的方式来做，结果是 int 类型。
• x << 1 等价于 x *= 2
• x << n 等价于 x *= 2ⁿ
• 一个数**每左移1位，等价于乘2**

1.2 >> 右移

• i >> j
  • 将 i 中的所有位向右移动 j 个位置，左边补 0；
  • 所有小于 int 的类型，移位以 int 的方式来做，结果是 int 类型。
  • 对于 unsigned 类型，左边补 0。对于signed类型的负数 i ，实际情况由具体实现来定义，有些是补0，有些是保留符号位补1
  • 对于 signed 类型，左边补原来的最高位数字（0或1，保持符号不变）
• x >> 1 等价于 x /= 2
• x >> n 等价于 x /= 2ⁿ
• 一个数**每右移1位，等价于除2**

int a = 0x80000000;
unsigned int b = 0x80000000;
printf("   a = %d\n", a);
printf("   b = %u\n", b);
printf("a>>16 = %d\n", a>>16);
printf("b>>16 = %u\n", b>>16);

输出结果：

1.3 注意

左移或右移的位数不要设置为负数，否则将导致未定义行为。

二、按位运算

按位运算符：

运算符	含义
&	按位与
`	`
~	按位取反
^	按位异或

2.1 &按位与

• 如果(x)_i == 1 且 (y)_i == 1，则 (x & y)_i = 1。否则 (x & y)_i = 0；
• 有0必为0，同是1才为1
• 和 0 相与 必为 0，和 1 相与 则不变

举例：
0101 1010 & 10001 100 = 0000 1000（5A & 8C = 08）

按位与常见应用：

• 让某一位或某些位为0：x & 0xFE（让x最低位为0）
• 取一个数中的一段： x & 0xFF（取x最低的1个字节，其余为0）

举例：
1010 0101 & 0xFE = A5 & FE = A4
1010 1010 1010 1010 & 0xFF = AAAA & FF = AA（125252 & FF = 252）

2.2 |按位或

• 如果(x)_i == 1 且 (y)_i == 1，则 (x | y)_i = 1。否则 (x | y)_i = 0；
• 有1必为1，同是0才为0
• 和 1 相或 必为 1，和 0 相或 则不变

按位与常见应用：

• 使得一位或几个位为1：x | 0x01（让x最低位为1）
• 把两个数拼接起来：0x00FF | 0xFF00 = 0xFFFF

2.3 ~按位取反

• ( ~x )_i = 1 - ( x )_i
• 01互换。

举例：
~1010 1010 = 0101 0101（~AA = 55）

按位取反与求补码不同：

• 按位取反是将各个位上的01翻转；
  • ~1010 1010 = 0101 0101
• 求补码：
  • 正数的补码等于原码；
  • 负数的补码，符号位不变，其余位取反后加1.

2.4 ^按位异或

• 如果 ( x )_i == ( y )_i，那么( x ^ y )_i = 0，否则为1；
• 相同为0，相异为1
• 对一个变量用同一个值异或两次，等于什么也没做。 x ^ y ^ y = x

2.5 逻辑运算和按位运算

逻辑运算与按位运算是不同的，不可混淆，但可以将逻辑运算视为将所有非0值变成1，再进行按位运算。

• 5 & 4 = 4  而 5 && 4 ——> 1 & 1 = 1
• 5 | 4 = 5   而 5 || 4 ——> 1 | 1 = 1
• ~4 = 3    而 !4 ——> !1 = 0

三、访问特定位

3.1 将特定位 置1

n |= 1<<j;			//将n的第j位 置1

const unsigned int BIT5 = 1u<<5;
n |= BIT5；			//将n的第5位 置1

3.2 将特定位 置0

n &= ~(1<<j);		//将n的第j位 置0

const unsigned int BIT5 = 1u<<5;					//此处也可使用宏定义
n &= ~BIT5；			//将n的第5位 置0

3.3 测试特定位 的值

//测试n的第j位是否为1
if( n & 1<<j ){
	...
}

• 左移运算符<<的优先级高于按位与运算符&

四、位域 （bit field）

位域 —— 一组连续的位

4.1 获取位域

（1）获取最右端的位域：

举例：获取第0~2位

//方法1：
j = i & 0x0007;						//获取第0~2位

//方法2：
const unsigned int BIT02 = 1u | 1u<<1 | 1u<<2
j = i & BIT02;

（2）获取其他位置的位域：

• 先将所需位域移动到最右端，再获取右端的位域

举例：获取第4~6位

j = (i>>4) & 0x0007;				//获取第4~6位

4.2 修改位域

修改位域的步骤：
- 清除位域（相关位清零，按位与&）；
- 设置位域（按位或|）。

举例：将第4~6位设为101

i = i & ~0x0070 | 0x0050;		//先按位与,相关位清零,再按位或设置目标值

注意：设置位域之前必须先将相关位清零。
例如上例中，若不清零，则只是将第4位和第6位设为1，而第5位不变。

五、结构中的位域

信息存储时不需要占用一个完整的字节，只需要占用一个或几个二进制位，结构中使用:表示位域。

5.1 位域的声明

声明格式：

struct 位域结构标记 {
	类型说明符 位域名 : 位域长度；
};

举例：MS-DOS操作系统使用16个二进制位存储日期。

//位域声明
struct file_date{
	unsigned int year : 7;				//占7个二进制位, year为此位域的位域名称
	unsigned int month : 4;
	unsigned int day : 5;
};

//简化声明
struct file_date {unsigned int year: 7, month: 4, day: 5; };

//位域的访问与修改
struct file_date fd;
fd.year = 42;			//2022年
fd.month = 8;
fd.day = 10;

scanf("%u", &fd.year);		//非法
printf("%u", fd.year);		//合法

• DOS中将1980年视为起始年份，因此只需7位二进制即可表示年份，year 中存储的是偏移值。
• 位域类型必须是 int，unsigned int，或 signed int。使用 int 可能会引起二义性，因为某些编译器会将位域的最高位视为符号位。
• 将所有的位域统一声明为unsigned int或signed int可以提高可移植性。
• 注意： 位域没有地址，可以使用取结构成员的方式（.运算符）访问或修改位域，但无法通过地址访问。
• 由于内存对齐，上述例子中，sizeof(file_date) = 4 。
• 位域名可省略

5.2 位域的存储

• 编译器将位域逐个放入存储单元中，相邻的同类型位域之间没有空隙，直到剩下的空间不够存放下一个位域。
• 此时，某些编译器会跳转到下一个存储单元再存储下一个位域，某些编译器会将此位域拆开，跨单元存放。（由实现来定义）
• 位域的存放顺序也依据大小端决定。
• C语言允许省略位域名，未命名的位域常用于字段间的填充，以保证其他位域存放在适当的位置。
• 位域长度可以为0

struct s {
	unsigned int a : 4;
	unsigned int : 0;
	unsigned int b : 8;
};

长度为0的位域，可以使编译器将下一个位域在一个存储单元的起始位置对齐。

5.3 位域的内存对齐

5.3.1 同类型位域

//sizeof(s1) == 1
struct s1{
	char a : 2;
	char b : 3;
	char c : 1;
} s1;

//sizeof(s2) == 2
struct s2 {
	char a : 2;
	char b : 3;
	char c : 7;				//调转到第2个存储单元存储
} s2;

5.3.2 不同类型位域

//sizeof(s3) == 12
struct s3 {
	char a : 2;
	int b : 2;				//粒度为4
	char c : 2;
} s3;

//sizeof(s4) == 12
struct s4 {
	char a : 2;
	char b : 2;				//a,b在第一个存储单元
	long c : 2;				//c在第2个存储单元
	char d : 2;				//d在第3个存储单元
} s4;

5.4 应用举例：修改位域

void prtBin(unsigned int number);
struct U0{
	unsigned int leading : 3;	//成员后的冒号:后的数是该成员所占比特数，从低位开始
	unsigned int FLAG1 : 1;
	unsigned int FLAG2 : 1;
	int trailing : 27;			//保证总共占32位,unsigned int所占位数
};

int main(){
	struct U0 uu;
	uu.leading = 2;
	uu.FLAG1 = 0;
	uu.FLAG2 = 1;
	uu.trailing = 0;
	printf("sizeof(uu)=%lu\n", sizeof(uu));
	prtBin(*(int*)&uu);		//将uu内的数据强制转换为int类型(本来是struct U0类型)
	
	return 0;
}

void prtBin(unsigned int number)
{
	unsigned mask = 1u<<31;
	for(; mask; mask >>=1){
		printf("%d", number & mask ? 1:0);
	}
	printf("\n");
}

输出结果：

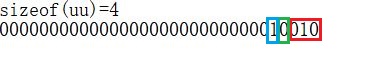
说明：

• 最低的3位为uu.leading = 2，其次为 uu.FLAG1 = 0，uu.FLAG2 = 1。其余为 uu.trailing = 0。
• 若结构定义里 trailing 改为占据28位，则总结构位数超过32位，编译器会增加一个 int，输出的 sizeof(uu) = 8 。

注意

• 将特定位组合成位域之后，可直接通过位域名称来访问。比移位、与、或更方便
• 编辑器会安排其中的位的排列，不具有可移植性，例如某些编辑器从最右端的位开始，有些从最左端开始。
• 当所需的位超过一个 int 时，会采用多个 int。

六、位运算举例

6.1 输出一个数的二进制数

int number;
scanf("%d", &number);
unsigned mask = 1u<<31;		//unsigned与变量之间省略类型,默认是unsigned int类型
							//1u表示为unsigned int类型的1
							//1u<<31 = 10000...00(31个0)
unsigned short bin = 0;
//跳过前面的0
for( ;mask ; mask >>= 1){
	bin = number & mask ? 1 : 0;
	if(bin) break;
}
							
for(; mask; mask>>=1){		//mask右移1位
	bin = number & mask ? 1 : 0;
	printf("%u", bin);
}
printf("\n");

6.2 控制一个数的特定位

const unsigned int SBS = 1u<<2;		//SBS = 00...0100
const unsigned int PE = 1u<<3;		//PE = 00...01000

U0LCR |= SBS | PE;			//让U0LCR的第2位和第3位为1,其余位不变(SBS|PE = 00...01100)
U0LCR &= ~(SBS | PE);		//让U0LCR的第2位和第3位为0,其余位不变

6.3 XOR加密

将每一个字符(ASCII码)与一个密钥进行异或(XOR)运算，实现简单的数据加密。

#include <ctype.h>				//isprint,判断是否为打印字符
#include <stdio.h>

const char KEY = '&';	//密钥

int main(){
	int orig_char, new_char;
	
	while((orig_char = getchar()) != EOF){
		new_char = orig_char ^ KEY;
		if(isprint(orig_char) && isprint(new_char))
			putchar(new_char);
		else
			putchar(orig_char);
	}
	
	return 0;
}

6.4 查看二进制的 0 / 1 的个数

6.4.1 查看 1 的个数

//方法1：移位法
int count1(int x)
{
	int cnt = 0;
	while(x){
		cnt += (x & 0x01);
		x >>= 1;
	}
	return cnt;
}

//方法2：消1法
int count1(int x)
{
	int cnt = 0;
	while(x){
		cnt++;
		x &= (x-1);
	}
	return cnt;
}

• 方法1的时间复杂度为 O(log₂x)，log₂x为x的二进制数的位数
• 方法2的时间复杂度为 O(M)，M为x的二进制数中1的个数。方法2的时间复杂度更低。

方法1的思路：
  每次将x右移一位，不断判断最低位是否为1

方法2的思路：
  通过x &= (x-1)将 x 的最右端的1（不一定是第0位）变为0，每消除一次最右端的1，记一次数，直到1完全消除，此时x=0。

6.4.2 查看 0 的个数

int count0(int x)
{
	int cnt = 0;
	while(x+1){
		cnt++;
		x |= (x+1);
	}
	return cnt;
}

思路：
  通过x |= (x+1)将x最右侧的0变为1，直至全1，循环结束。
全1时，x = -1 。全1就是-1的补码，保证加1后结果为0。

补充：如何通过补码求真值

• 判断是有符号数还是无符号数
• 若是无符号数：
  • 补码 = 原码，直接求真值
• 若是有符号数：由最高位判断正数还是负数
  • 正数：补码 = 原码，直接求
  • 负数：补码减1，得反码，然后全部按位取反(含符号位)，求得相应正数的原码，由此原码计算该正数，取相反数即为真值。