简单二叉树 - Java实现

前言

因为是简单二叉树的创建，那么就需要自己输入二叉树各个节点的位置，使用先序创建二叉树。

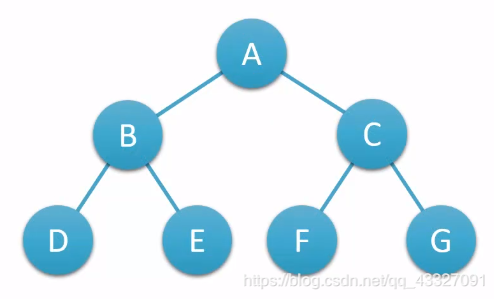
如果我想创建上图所示的二叉树，那么输入的顺序为：
{“A”, “B”, “D”, “#”, “#”, “E”, “#”, “#”, “C”, “F”, “#”, “#”, “G”, “#”, “#”}

代码实现

BinaryTree.java

import java.util.ArrayDeque;
import java.util.LinkedList;

public class BinaryTree<T> {

    private TreeNode<T> root;

    private static class TreeNode<T> {
        private T data;
        private TreeNode<T> leftChild;
        private TreeNode<T> rightChild;

        public TreeNode(T data) {
            this.data = data;
        }

        public TreeNode(T date, TreeNode<T> leftChild, TreeNode<T> rightChild) {
            this.data = date;
            this.leftChild = leftChild;
            this.rightChild = rightChild;
        }

        public T getData() {
            return data;
        }

        public void setData(T data) {
            this.data = data;
        }

        public TreeNode<T> getLeftChild() {
            return leftChild;
        }

        public void setLeftChild(TreeNode<T> leftChild) {
            this.leftChild = leftChild;
        }

        public TreeNode<T> getRightChild() {
            return rightChild;
        }

        public void setRightChild(TreeNode<T> rightChild) {
            this.rightChild = rightChild;
        }

        @Override
        public String toString() {
            return data + " ";
        }
    }

    public BinaryTree() {
        root = null;
    }

    // 建立树
    public void buildTree(LinkedList<T> list) {
        root = createTree(root, list);
    }

    // 使用先序遍历递归创建树
    private TreeNode<T> createTree(TreeNode<T> node, LinkedList<T> list) {

        String element = (String)list.removeFirst();

        if (element.trim().equals("#")) {
            return null;
        } else {
            node = new TreeNode<T>((T)element);
            node.setLeftChild(createTree(node.leftChild, list));
            node.setRightChild(createTree(node.rightChild, list));
            return node;
        }
    }

    // 先序遍历
    public void preOrder() {
        preOrder(root);
    }
    private void preOrder(TreeNode<T> root) {
        if (root != null) {
            System.out.print(root.data);
            preOrder(root.leftChild);
            preOrder(root.rightChild);
        }
    }

    // 中序遍历
    public void inOrder() {
        inOrder(root);
    }
    private void inOrder(TreeNode<T> root) {
        if (root != null) {
            inOrder(root.leftChild);
            System.out.print(root.data);
            inOrder(root.rightChild);
        }
    }

    // 后序遍历
    public void postOrder() {
        postOrder(root);
    }
    private void postOrder(TreeNode<T> root) {
        if (root != null) {
            postOrder(root.leftChild);
            postOrder(root.rightChild);
            System.out.print(root.data);
        }
    }

    // 非递归先序遍历 根-左-右
    // - 访问根结点，根结点进栈，遍历左孩子(循环访问)，如果左孩子为空，根结点出栈，遍历右孩子
    public void preOrder_() {
        preOrder_(root);
    }
    private void preOrder_(TreeNode<T> root) {
        ArrayDeque<TreeNode> stack = new ArrayDeque<>();
        TreeNode curr = root;
        while(curr != null || !stack.isEmpty()) {
            while(curr != null) {
                System.out.print(curr.data);
                stack.push(curr);
                curr = curr.leftChild;
            }
            if (!stack.isEmpty()) {
                curr = stack.pop();
                curr = curr.rightChild;
            }
        }
    }

    // 非递归中序遍历 左-根-右
    // - 根结点进栈，遍历左孩子(循环访问)，如果左孩子为空，访问根结点，根结点出栈，遍历右孩子
    public void inOrder_() {
        inOrder_(root);
    }
    private void inOrder_(TreeNode<T> root) {
        ArrayDeque<TreeNode> stack = new ArrayDeque<>();
        TreeNode curr = root;
        while(curr != null || !stack.isEmpty()) {
            while(curr != null) {
                stack.push(curr);
                curr = curr.leftChild;
            }
            if (!stack.isEmpty()) {
                curr = stack.pop();
                System.out.print(curr.data);
                curr = curr.rightChild;
            }
        }
    }

    // 非递归后序遍历
    // - 后序遍历难点在于：因为根结点是最后一次访问，我们需要判断当前访问结点的左子树是否
    // 被访问，右结点是否被访问，我们可以使用一个引用存储上一次访问的结点，如果上一次
    // 访问的结点是当前结点的右结点或者当前结点的右结点为空，那么就访问这个结点，否则
    // 就遍历当前结点的右子树
    public void postOrder_() {
        postOrder_(root);
    }
    public void postOrder_(TreeNode<T> root) {
        ArrayDeque<TreeNode> stack = new ArrayDeque<>();
        TreeNode curr = root;
        TreeNode pre = null;

        while(curr != null || !stack.isEmpty()) {
            // 存在左子树那么就遍历
            while(curr != null) {
                stack.push(curr);
                curr = curr.leftChild;
            }
            // 获得当前结点
            curr = stack.peek();
            // 当前结点访问的前提是：右子树为空，或者已被访问
            if (curr.rightChild == null || curr.rightChild == pre) {
                System.out.print(curr.data);
                stack.pop();
                pre = curr;

                // 如果当前结点被访问，那么就会出栈，置为null，会遍历当前结点的父结点
                curr = null;
            } else {
                curr = curr.rightChild;
            }
        }
    }

    // 层序遍历
    public void levelOrder() {
        levelOrder(root);
    }
    private void levelOrder(TreeNode<T> root) {
        ArrayDeque<TreeNode> queue = new ArrayDeque<>();
        TreeNode curr = root;

        if (curr == null)
            return;
        queue.add(curr);

        while (!queue.isEmpty()) {
            curr = queue.remove();
            System.out.print(curr.data);
            if (curr.leftChild != null)
                queue.add(curr.leftChild);
            if (curr.rightChild != null)
                queue.add(curr.rightChild);
        }
    }

    // 统计二叉树叶子结点的个数
    public int getLeafNodes() {
        return getLeafNodes(root);
    }
    private int getLeafNodes(TreeNode<T> root) {
        if (root.leftChild == null && root.rightChild == null)
            return 1;
        return getLeafNodes(root.leftChild) + getLeafNodes(root.rightChild);
    }
    
    // 计算树的深度 - 递归遍历左右子树
    public int getDepth() {
        return getDepth(root);
    }
    private int getDepth(TreeNode<T> root) {
        return root == null ? 0 : (1 + Math.max(getDepth(root.leftChild), getDepth(root.rightChild)));
    }
    
}

注意：我们可以看到每个方法都有重载了一个私有、一个公有方法，这样是为了将公有给外界使用，具体的实现细节留在私有方法里面。

BinaryTreeTest.java

import java.util.LinkedList;

public class BinaryTreeTest {

    public static void main(String[] args) {
        BinaryTree<String> tree = new BinaryTree<>();
        LinkedList<String> linkedList = new LinkedList<>();
        String[] strings = {"A", "B", "D", "#", "#", "E", "#", "#", "C", "F", "#", "#", "G", "#", "#"};
        for (String str :
                strings) {
            linkedList.add(str);
        }
        tree.buildTree(linkedList);
        System.out.println("先序遍历:");
        tree.preOrder();
        System.out.println();
        tree.preOrder_();
        System.out.println();

        System.out.println("中序遍历:");
        tree.inOrder();
        System.out.println();
        tree.inOrder_();
        System.out.println();

        System.out.println("后续遍历");
        tree.postOrder();
        System.out.println();
        tree.postOrder_();
        System.out.println();

        int num = tree.getLeafNodes();
        System.out.println("叶子结点个数：" + num);

		int depth = tree.getDepth();
        System.out.println("树的深度：" + depth);
    }
}