- 声明:仅为个人学习笔记,如有误及侵权请私信联系
1、分类
Logistic要解决的问题:预测变量y是离散值情况下的分类。
特点:算法的输出/预测值一直介于[0,1]之间。
逻辑(Logistic)回归,虽然叫做回归,但是一种分类算法,“回归”只是由于历史缘故得名。
2、假设陈述
线性回归假设函数hθ(x)=θTx,Logistic回归假设g(z)=1/(1+e^(-z))
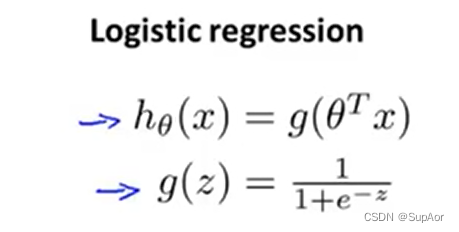
g(z)也成为sigmoid函数
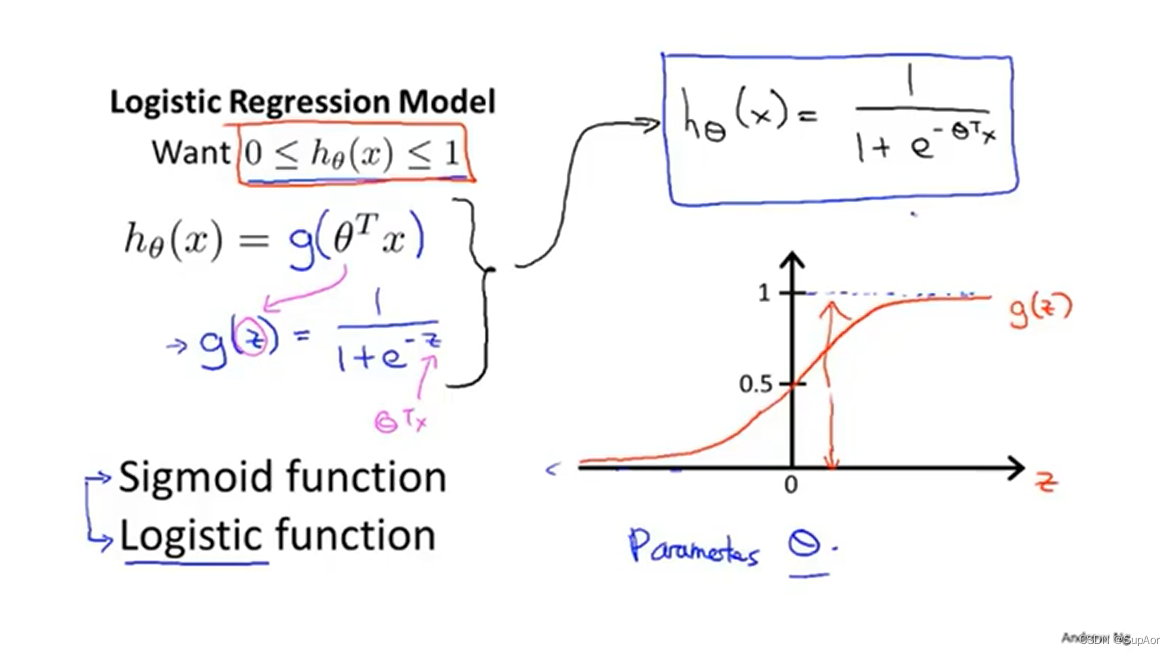 假设例子:
假设例子:

3、决策界限
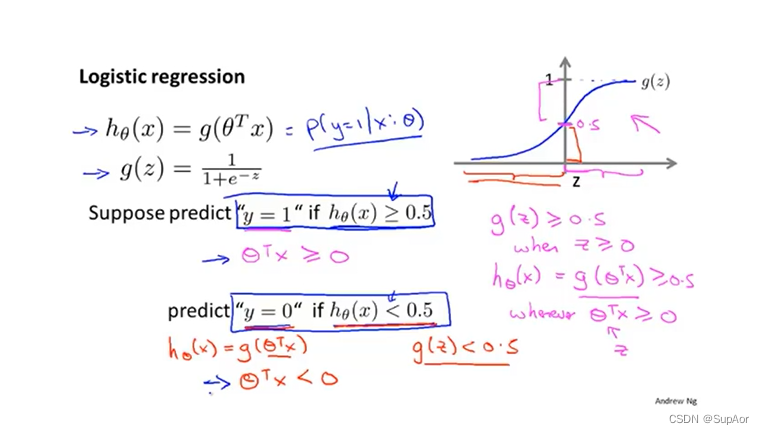
决策公式:
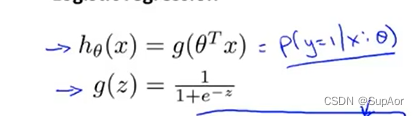
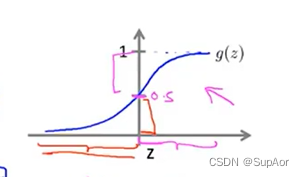
由决策公式,结合sigmoid函数图像,
若要g(z)>=0.5,则z>0,即θT>=0
g(z)<0.5,则z<0,即θT<0.
 假定条件,利用sigmoid函数,得到x1+x2的范围,令其等于0求解交点。本例中直线x1+x2=3将两个区域分隔开,这条直线被称为决策边界。
假定条件,利用sigmoid函数,得到x1+x2的范围,令其等于0求解交点。本例中直线x1+x2=3将两个区域分隔开,这条直线被称为决策边界。
此时x1+x2=3对应假设函数预测y=0.5的情况,直线一端假设函数预测y=0,另一端假设函数预测为y=1.
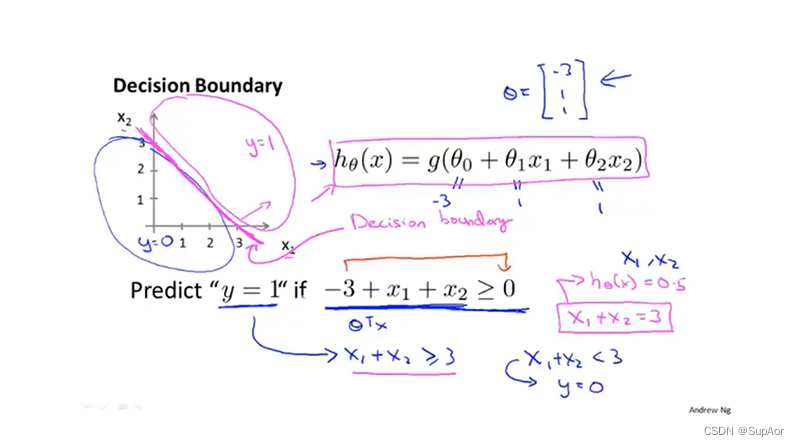
更复杂情况下,可以增加参数:

注意:决策边界不是训练集的属性,而是假设本身及其参数的属性!!!θ确定后,决策边界就确定了。使用训练集来确定θ。
4、代价函数
给定假设,有Question如何拟合参数θ:

目前存在的问题,现在的代价函数不是线性函数,假设函数变成了sigmoid函数,所以如果再想使用梯度下降法,比一定能找到全局最优点,可能只是局部最优,图一是非凸函数,图二是凸函数。
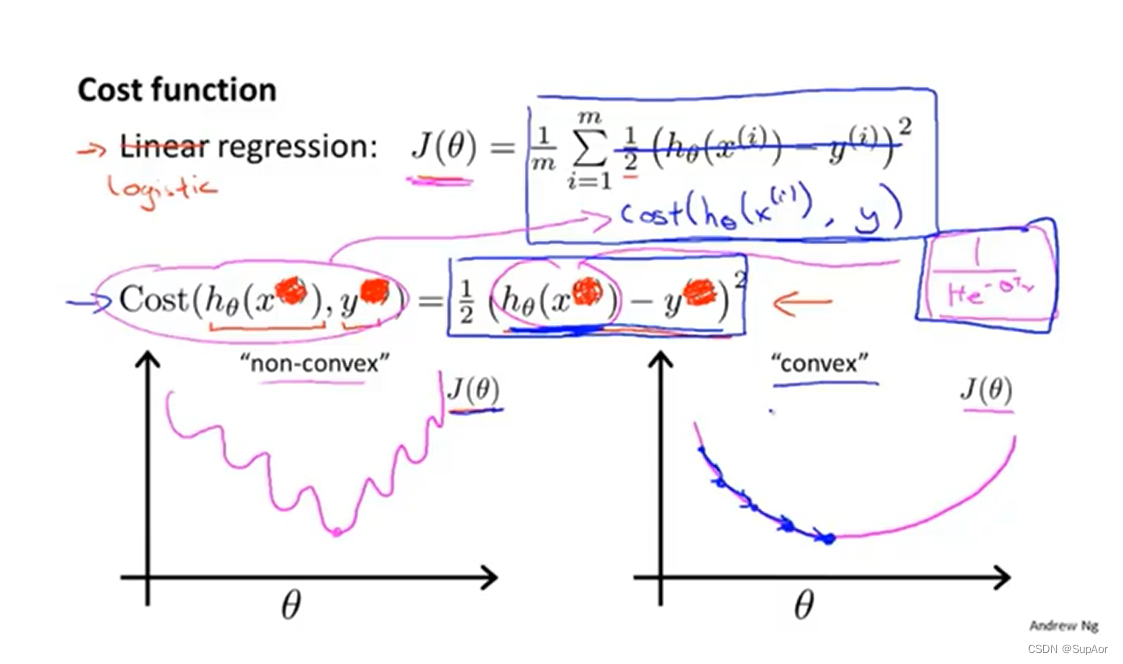 代价函数定义:
代价函数定义:


当y=1时,如果hθ(x)=0,则Cost=0
但是当hθ(x)–>0,则Cost–>oo
故而如果预测有误,则会赋予一个巨大的代价来惩罚这个学习算法
当y=0时,如果hθ(x)=0,则Cost=0
但是当hθ(x)–>1,则Cost–>oo
故而如果预测有误,则会赋予一个巨大的代价来惩罚这个学习算法
5、简化代价函数与梯度下降

上式当y=1时消掉一项,当y=0时消掉另一项。
Step:
 主要目标是怎样使J(θ)最小化。
主要目标是怎样使J(θ)最小化。
最小化代价函数的方法是使用梯度下降法
 线性回归和逻辑回归利用梯度下降法计算的公式一致,仅仅是假设函数不一样。
线性回归和逻辑回归利用梯度下降法计算的公式一致,仅仅是假设函数不一样。

线性回归中特征缩放提高梯度下降的收敛速度的方法在logistics中同样适用。
6、高级优化
高级优化算法优化:梯度下降、共轭梯度、BFGS、L-BFGS
后三种优化算法优点:
1、不需要手动选择;
2、收敛速度比梯度下降更快
后三种优化算法缺点:
1、比梯度下降法复杂
Example:

7、多元分类:一对多
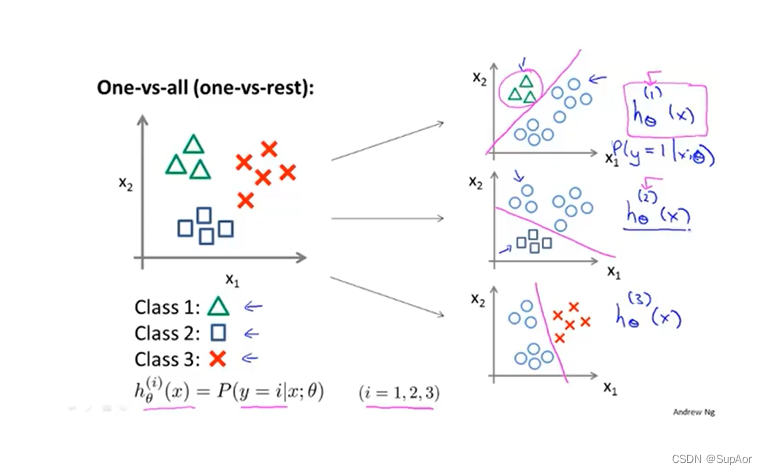 上例中,有三类,构造三个逻辑回归二分类分类器,预测i类别y=i的概率,最后,为了做出预测,我们可以给出一个新的输入值x,期望获得预测,我们要做的就是在三个分类器中运行输入x,选择使h最大的类别,即:置信度、可信度最高的分类器,作为最终分类器。
上例中,有三类,构造三个逻辑回归二分类分类器,预测i类别y=i的概率,最后,为了做出预测,我们可以给出一个新的输入值x,期望获得预测,我们要做的就是在三个分类器中运行输入x,选择使h最大的类别,即:置信度、可信度最高的分类器,作为最终分类器。
8、Logistic回归python编程实战
在训练的初始阶段,我们将要构建一个逻辑回归模型来预测,某个学生是否被大学录取。设想你是大学相关部分的管理
者,想通过申请学生两次测试的评分,来决定他们是否被录取。现在你拥有之前申请学生的可以用于训练逻辑回归的训
练样本集。对于每一个训练样本,你有他们两次测试的评分和最后是被录取的结果。为了完成这个预测任务,我们准备
构建一个可以基于两次测试评分来评估录取可能性的分类模型。
8.1导入数据并查看特征
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = 'ex2data1.txt'
data = pd.read_csv(path,header=None,names = ['Exam 1','Exam 2','Admitted'])
data.head()
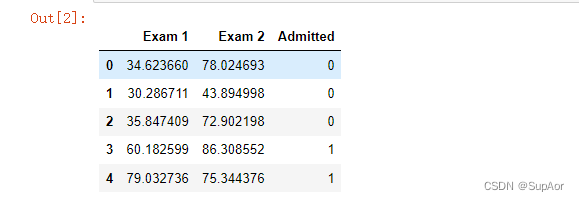
创建两个分数的散点图,可视化,定义正样本是录取,负样本是未录取:
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig ,ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['Exam 1'],positive['Exam 2'],s = 50,c='b',marker='o',label = 'Admitted')
ax.scatter(negative['Exam 1'],negative['Exam 2'],s = 50,c='r',marker='o',label = 'Not Admitted')
ax.legend()
ax.set_xlabel('Exam 1 score')
ax.set_xlabel('Exam 2 score')
plt.show()
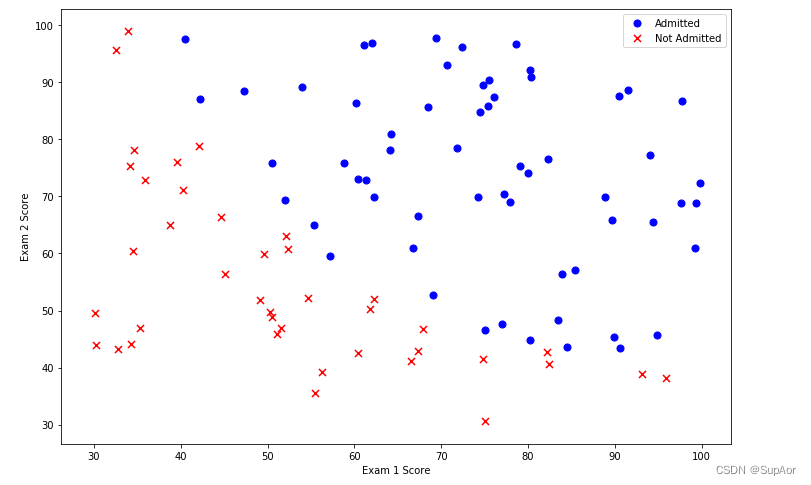 看起来在两类间,有一个清晰的决策边界。现在我们需要实现逻辑回归,那样就可以训练一个模型来预测结果。
看起来在两类间,有一个清晰的决策边界。现在我们需要实现逻辑回归,那样就可以训练一个模型来预测结果。
8.2 引入sigmoid函数
 定义sigmoid函数:
定义sigmoid函数:
def sigmoid(z):
return 1/(1+np.exp(-z))
画图测试sigmoid函数是否能用:
nums = np.arange(-10,10,step=1)
fig,ax =plt.subplots(figsize=(12,8))
ax.plot(nums,sigmoid(nums),'r')
plt.show()
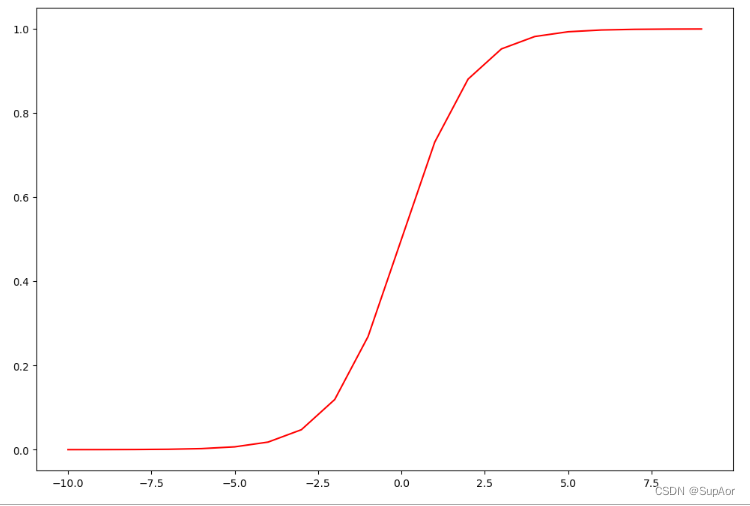 编写代价函数来评估结果:
编写代价函数来评估结果:
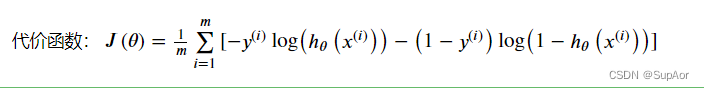
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
return np.sum(first - second) / (len(X))
现在,我们要做一些设置,和我们在练习1在线性回归的练习很相似。包括矩阵转换调整:
# add a ones column - this makes the matrix multiplication work out easier
data.insert(0, 'Ones', 1)
# set X (training data) and y (target variable)
cols = data.shape[1]
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]
# convert to numpy arrays and initalize the parameter array theta
X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(3)
检查矩阵维度:
X.shape,theta.shape,y.shape
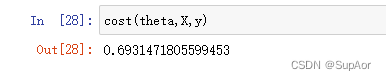
 计算代价:
计算代价:
cost(theta,X,y)





 文章介绍了Logistic回归的基本概念,包括分类问题、假设陈述、决策边界的确定、代价函数及其简化、梯度下降优化方法。此外,还探讨了多元分类问题,并提供了一个使用Python进行Logistic回归编程实战的例子,包括数据导入、sigmoid函数的实现以及代价函数的计算。
文章介绍了Logistic回归的基本概念,包括分类问题、假设陈述、决策边界的确定、代价函数及其简化、梯度下降优化方法。此外,还探讨了多元分类问题,并提供了一个使用Python进行Logistic回归编程实战的例子,包括数据导入、sigmoid函数的实现以及代价函数的计算。

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










