逻辑回归--机器学习基础

---

逻辑回归

logistic回归是一种广义线性回归（generalized linear model），因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 w‘x+b，其中w和b是待求参数。

---

一、逻辑回归中的条件概率

1.1逻辑回归的应用

  逻辑回归是二分类问题的神器，非常简单实用，是在线上系统中使用率最高的模型。

经典的二分类问题有
预测贷款违约情况（违约/不会违约）

情感分析（正面/负面）

预测广告点击率（会点击/不会点击）

预测疾病（阳性/阴性）

1.2理解基准

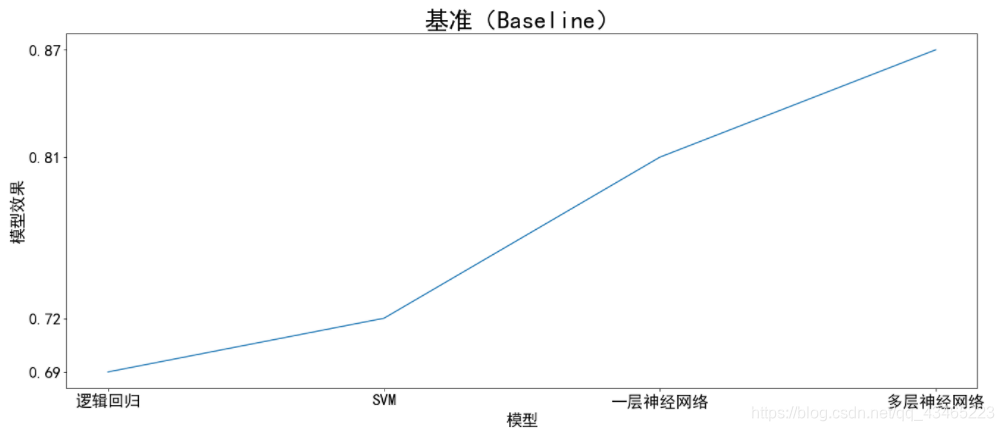
基准（Baseline）：逻辑回归是很靠谱的基准（Baseline），搭建任何分类模型是首先可以考虑逻辑回归，之后在逐步尝试更复杂的模型。

  基准(baseline)在建模过程中非常重要。简单来讲,在设计模型的阶段,首先试图通过简单的方法来快速把系统搭起来,之后逐步把模块细化,从而不断得到更好的解决方案。对于分类任务, 逻辑回归 模型可以称得上是最好的基准,也是比较靠谱的基准。

例如：最开始选取逻辑回归最为模型，模型效果为0.69，然后进行优化，选择SVM，发现为0.72，有所提升，进一步更换为一层神经网络，变为0.81，从而判断是否还需要进一步的进行优化，（这里我的数字是我举例随便想的），假如当使用多层神经网络模型参数为0.82，那么我们就可以判断我们没有必要再使用同一方法继续优化下去。

1.3分类问题

例如：
学习输入到输出的映射：
$$F:X\to y$$
由年龄、工资、学历三个特征，来腿短还款是否逾期

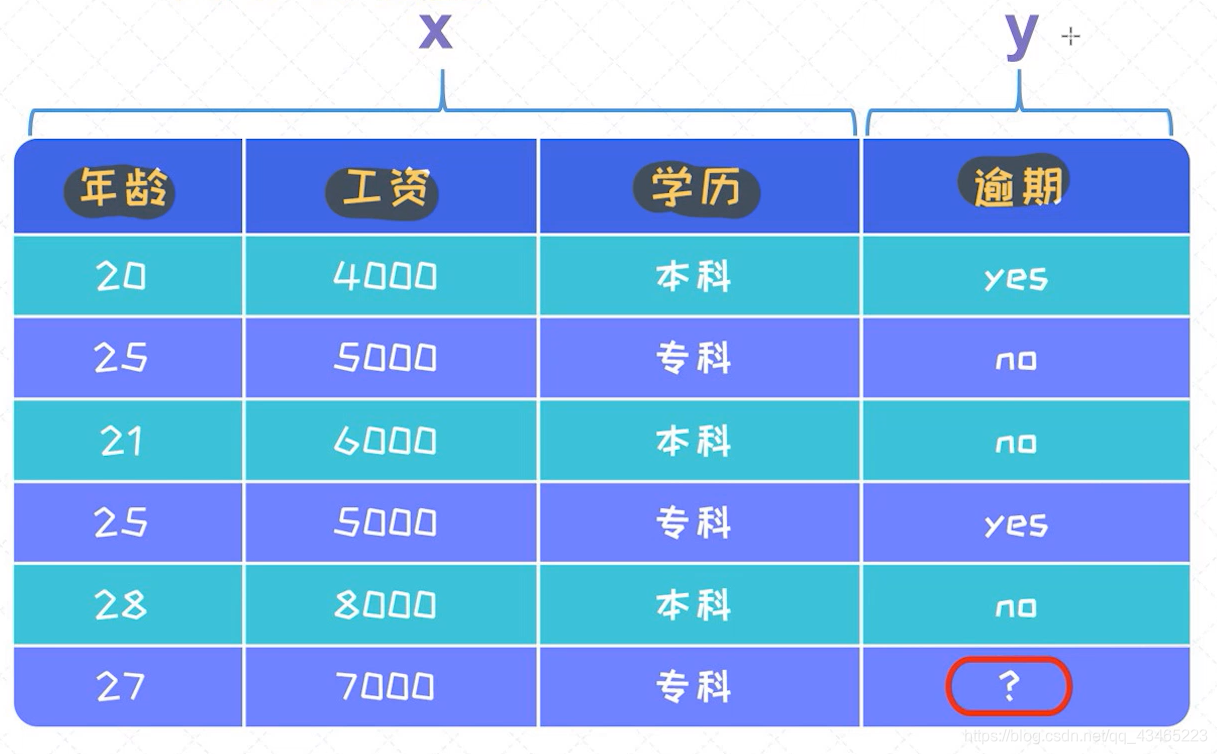
假如我们有办法表示条件概率：
$$P(Y=0|X)和P(Y=1|X)$$

可设计分类规则：
if P（y=0|x）> P(y=1|x) :
 y=0
else:
 y = 1

  从X到y的映射关系是通过上述的条件概率所表示的。

  这里的核心问题是:如果通过 条件概率 p(y|x)来描述xx和yy之间的关系。 逻辑回归 实际上是基于线性回归模型构建起来的,所以这里也希望通过 线性回归 方程 一步步来构造上述的条件概率p(y|x)。

作为概率，有以下性质
$$\begin{gathered} 0<=P(Y=0|X)<=1① \\ 0<=P(Y=1|X)<=1② \\ P(Y=0|X)+P(Y=1|X)=1③ \end{gathered}$$
如何把正无穷到负无穷区间的值映射到(0,1)区间?只要有方法做到这一点,我们就可以表示成概率了

1.4逻辑函数

逻辑函数又叫sigmoid函数

  逻辑函数的应用非常广泛,特别是在神经网络中处处可见,很大程度上是源于它不可或缺的性质:可以把任意区间的值映射到(0,1)区间。这样的值既可以作为概率,也可以作为一种权重。另外,由于大多数模型在训练时涉及到 导数 (derivative)的计算,同时逻辑函数的导数具有极其简单的形态,这也使得逻辑函数受到了很大的欢迎。
$$\begin{gathered} y=\frac{1}{1+e^{-x}} \\ 定义域（-\infty ,+\infty ） \\ 值域（0,1） \end{gathered}$$

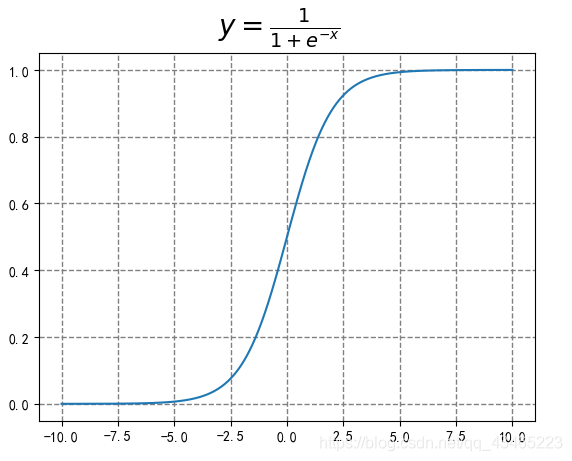
# sigmoid函数使用python matplotlib代码
import numpy as np 
import matplotlib.pyplot as plt 
# 生成x的范围
x = np.arange(-10, 10, 0.001)
y = 1 / (1 + np.exp(-x))
# 创建画布
plt.figure
# 使用折线图画出
plt.plot(x,y)
# 使用lateX语法表示公式
plt.suptitle(r'$y=\frac{1}{1+e^{-x}}$', fontsize=20)
# 添加网格
plt.grid(color='gray')
plt.grid(linewidth='1')
plt.grid(linestyle='--')
# 显示图像
plt.show()

逻辑函数的倒数

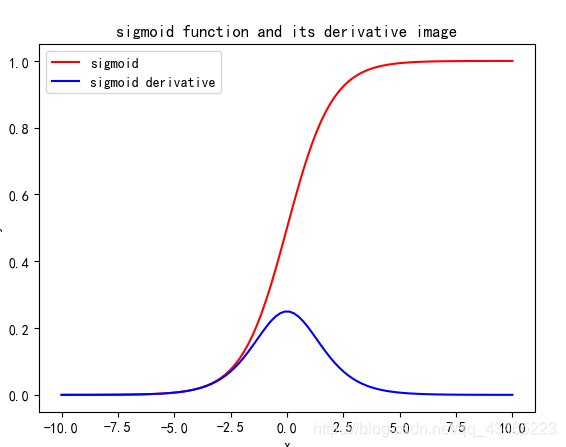
import numpy as np
import matplotlib.pyplot as plt 
# sigmoid_and_Derivative.py
x=np.linspace(-10,10,100)
y=1/(1+np.exp(-x))
plt.xlabel("x")
plt.ylabel("y")
plt.title("sigmoid function and its derivative image")
plt.plot(x,y,color='r',label="sigmoid")
y=np.exp(-x)/pow((1+np.exp(-x)),2)
plt.plot(x,y,color='b',label="sigmoid derivative")
plt.legend()#将plot标签里面的图注印上去
plt.show()

1.5样本的条件概率

当把 线性回归 的式子和逻辑函数拼在一起的时候,就可以得到合理的 条件概率 的表达式。

新的条件概率
逻辑函数：$y=\frac{1}{1+e^{-x}}$
不合理的条件概率$P(Y|X)=W^T\times X+b$
新的条件概率$$y=\frac{1}{1+e^{-(W^T\times X+b)}}$$

  在 逻辑回归 中我们针对的是 二分类问题 ,所以一个样本必须要属于其中的某一个分类。这就意味着, 条件概率 p(y=1|x)p(y=1∣x)和p(y=0|x)p(y=0∣x)之和一定会等于1。

可以将上述的两个式子合并为一个
$$P(Y|X)=(\frac{1}{1+e^{-(W^T\times X+b)}}{)}^y(1-\frac{1}{1+e^{-(W^T\times X+b)}}{)}^{1-y}$$
可以验证一下当 y=1 时和 y=0时，正好与上述相同。

二、逻辑回归的目标函数

2.1最大似然估计

  最大似然估计(Maximum Likelihood Estimation)在机器学习建模中有着举足轻重的作用。它可以指引我们去构造模型的目标函数,以及求出使 目标函数 最大或者最小的参数值。
  一个比较抽象的解释是:假如有个未知的模型(看作是黑盒子),并且它产生了很多能观测到的样本。这时候,我们便可以通过最大化这些样本的概率反过来求出模型的 最优参数 ,这个过程称之为最大似然估计。

注意：这里研究生入学考试数学一会考，课参考汤家凤的视频
原理：
  给定一个概率分布D，假定其概率密度函数（连续分布）或概率聚集函数（离散分布）为fD，以及一个分布参数θ，我们可以从这个分布中抽出一个具有n个值的采样X1,X2,…,Xn，通过利用fD，我们就能计算出其概率：

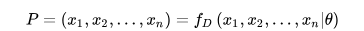
  但是，我们可能不知道θ的值，尽管我们知道这些采样数据来自于分布D。那么我们如何才能估计出θ呢？一个自然的想法是从这个分布中抽出一个具有n个值的采样X1,X2,…,Xn，然后用这些采样数据来估计θ。
一旦我们获得，我们就能从中找到一个关于θ的估计。最大似然估计会寻找关于 θ的最可能的值（即，在所有可能的θ取值中，寻找一个值使这个采样的“可能性”最大化）。这种方法正好同一些其他的估计方法不同，如θ的非偏估计，非偏估计未必会输出一个最可能的值，而是会输出一个既不高估也不低估的θ值。
要在数学上实现最大似然估计法，我们首先要定义可能性：

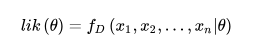
  并且在θ的所有取值上，使这个函数最大化。这个使可能性最大的值即被称为θ的最大似然估计。

2.2逻辑回归的似然函数

  对于单个样本的 条件概率 已经定义过了,这个概率也可以看作是似然概率。下一步得把所有的样本全部考虑进来,这时候我们得到的就是所有样本的似然概率。
$$P(Yi|Xi;w,b)=p(Yi=1|Xi;w,b{)}^{Yi}[1-(Yi=1|Xi;w,b){]}^{1-Yi}$$
整个样本的似然概率
$$\prod _{i=0}^{n}P(Yi|Xi;w,b)$$
有了所有样本的 似然概率 之后,我们的目标就是要求出让这个似然概率最大化的模型的参数(对于逻辑回归模型就是w,bw,b)。这个过程称之为最大似然估计(maximum likelihood estimation)。

2.3逻辑回归的最大似然估计

我们需要最大化目标函数

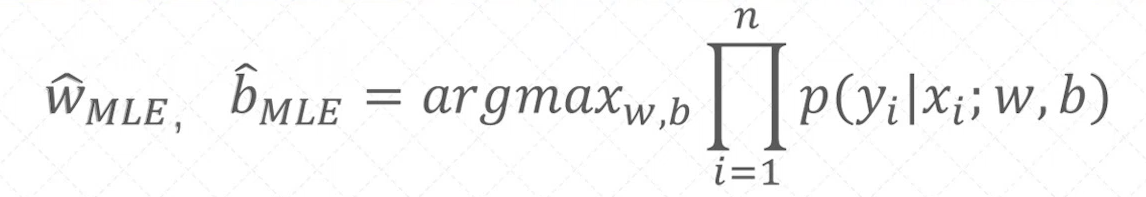
得到了逻辑回归的目标函数之后,首先来做一层简化,就是把乘积的形式改造成加法形式。这对于后续的运算有很大的帮助

根据高中数学知识，将乘积整体取对数，就可以变为乘积的形式，
把乘积转换成累加之和，并改成最小化的问题：

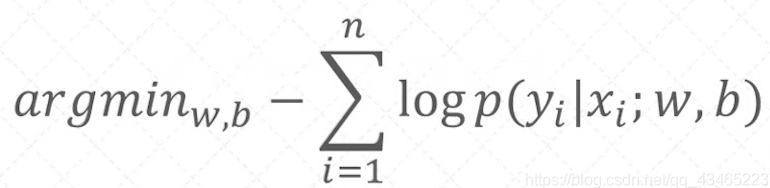
接下来就是从这个函数中求得最小值，也就是w,b的最优解，下篇文章将介绍梯度下降法。具体介绍梯度下降法求解目标函数！

总结

本文主要讲了逻辑回归的一些内容。