数塔（简单dp）

最新推荐文章于 2022-07-01 09:09:51 发布

原创

最新推荐文章于 2022-07-01 09:09:51 发布 · 4.3k 阅读

9 ·

CC 4.0 BY-SA版权

数塔问题是一个经典的动态规划算法实例，要求从顶层走到底层，每步只能走到相邻结点，目标是使经过的结点数字之和最大化。给定数塔的高度和每一层的数字，通过动态规划策略，可以找到从顶层到底层的最大路径和。动态规划通过拆分问题，定义状态并递推求解，保留可能最优的局部解，最终得到全局最优解。

数塔

在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：

有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？
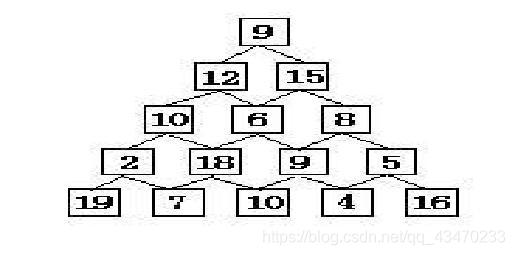
在这里插入图片描述

已经告诉你了，这是个DP的题目，你能AC吗?
Input
输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。
Output
对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。
Sample Input
1
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
30

动态规划：就是把一个复杂的问题划分成无数个子问题，保证每一个子问题的最优解，即动态规划算法是通过拆分问题，定义问题状态和状态之间的关系，使得问题能够以递推（或者说分治）的方式去解决。 [1]
动态规划算法的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

这道题的思路就是从下往上依次取每一个位置连接的下方两个数中较大的数做和，即顶层最后的值就是从顶层到底层可能得到的最大的值

ac代码