matlab解决无约束优化问题

无约束优化问题

要用到的数学知识：
1、向量范数与矩阵范数
2、多元函数梯度与Hessian阵
3、凸集与凸函数
特别要提示的是：如果该函数为凸函数，那么它有且仅有一个最优点，如果它的值不在无穷处，我们利用大部分算法都可以很容易找到它。
范数

无约束优化算法

在数值优化中，一般采用迭代法求解无约束优化问题，所用到算法大致可分为：线搜索方法，信 赖域方法，最小二乘问题的Gauss-Newton法、L-M方法。其中线搜索方法用的较多，主要有梯度法（也称最速下降法），牛顿法，共轭梯度法，拟牛顿法。
首先来看无约束优化问题。无约束优化问题中会需要极值点分析,如局部最
小（大)点、全局最小(大)点以及拐点（例如$x^3$在$x=0$时）。高等数学有讲过,简单的函数求极值点可以求梯度,复杂一点的可以求二阶偏导,得到$Hessian$ 矩阵。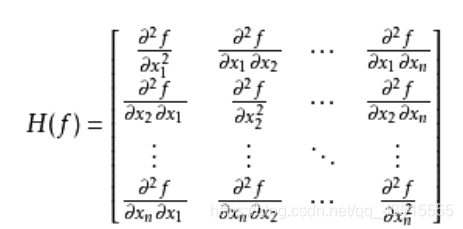
从$Hessian$矩阵可以看出$Hessian$矩阵是个对称矩阵,因此可以定义矩阵的正负,也就是求对应的二次型的正负。求解二次型的特征值,如果特征值全正, 就是正定矩阵;如果有正有负,就是不定矩阵。

泰勒级数

展开
泰勒展开特别有用,可以很方便的把一个函数展开成幂级数,即从函数的线性近似来估计函数。

（1）输入为标量的泰勒级数展开:如果是极值点,一阶导数一定为0;如果一阶导数$f^{’}\left(x_k\right)=0$,可以是极大点、极小点或者拐点。然后再求二阶导数$f^{’}\left(x_k\right)>0$, $x^k$为严格局部最小点,反之局部最大点,$f^{’}\left(x_k\right)=0$则可能是一
个鞍点。

牛顿切线法

牛顿法就是一种近似于泰勒级数展开的一种迭代接近求值的方法
由$f\left(x\right)=0$
$$f\left(x\right)\approx f\left(x_0\right)+f^{’}\left(x_0\right)\left(x-x_0\right)$$
可得$$x=x_0-\frac{f\left(x_0\right)}{f^{’}\left(x_k\right)}$$，将这个结果作为近似解，令$x_0=x$，便可得到迭代公式$$x_{k+1}=x_k-\frac{f\left(x_k\right)}{f^{’}\left(x_k\right)}$$

几何意义

当，那么它的根就代表了曲线与相交的横坐标。如果选定好了初始位置，那么在处的切线为，该切线与x轴的交点的横坐标为，再从做切线，然后找交点，再做切线…那么递推公式为，如下图

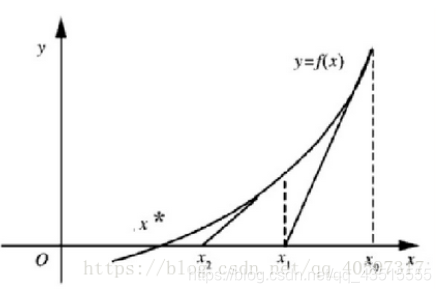
所示matlab代码供参考

`function y=newton(X,Y,x)
n=length(X);
m=length(x);
for h=1:m
    z=x(h);
    w=Y(1);
    for k=2:n
        s=0;
        for j=1:k
            p=1;
            for i=1:k
                if i~=j
                    p=p*(X(j)-X(i));
                end
            end
            s=s+Y(j)/p;
        end
        q=1;
        for j=1:k-1
            q=q*(z-X(j));
        end
        w=w+s*q;
    end
    y(h)=w;
end`

令导数为0,求得x,a的值后,将x带入f(x)即为在约束条件h(x)下的可行解。这样做的意义是什么呢?接下来看一个直观的示例,对于二维情况下
的目标函数是$f\left(x,y\right)$，在平面中画出$f\left(x,y\right)$的等高线,如下图的虚线所示,并
只给出一个约束等式$h\left(x,y\right)=0$如下图的绿线所示,目标函数$f\left(x,y\right)$与约
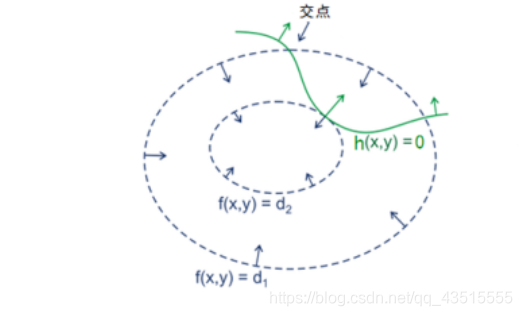
束$g\left(x,y\right)$只有三种情况,相交、相切或者没有交集,没交集肯定不是解，只有相交或者相切可能是解,但相交得到的一定不是最优值,因为在相交点的梯度方向（或负方向)走,等高线会变大（或变小）。而在相切点,沿着梯度方向（或负方向)走,等高线都会变大,这就意味着只有等高线与目标函数的曲线相切的时候,才可能得到最优解。

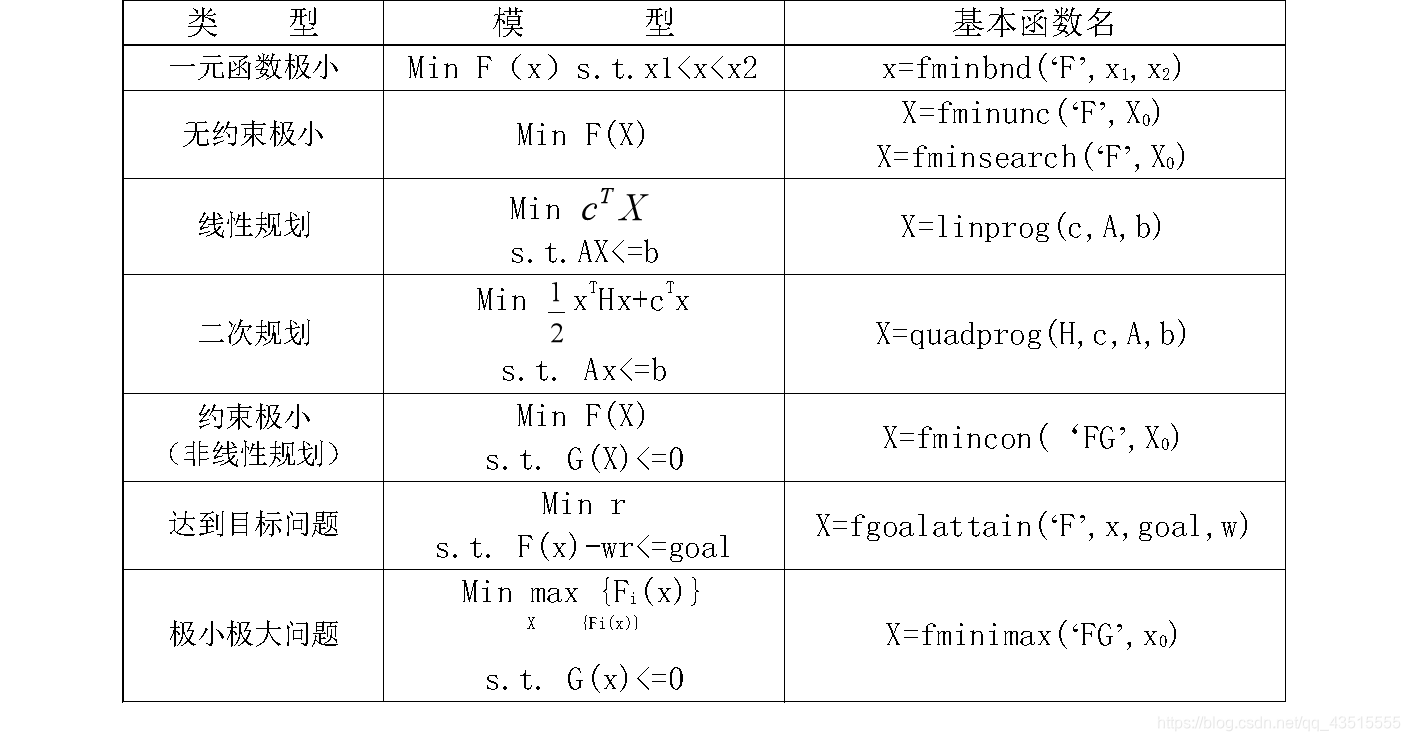
matlab求解优化问题的主要函数

：

优化函数的输入变量

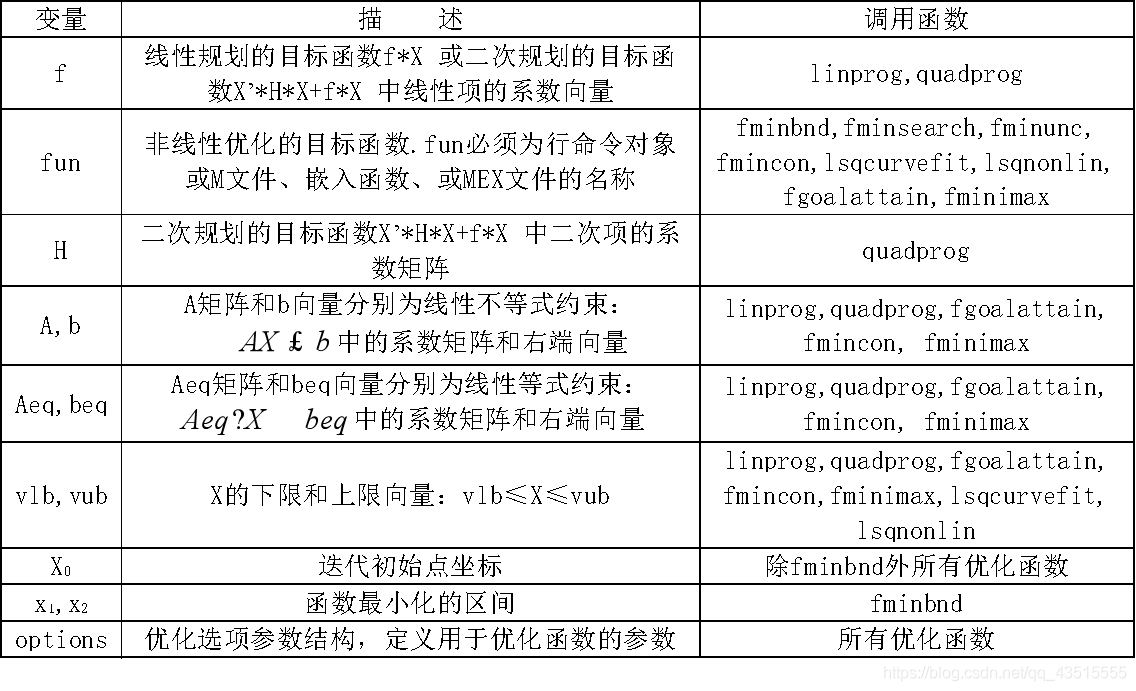
优化函数的输出变量

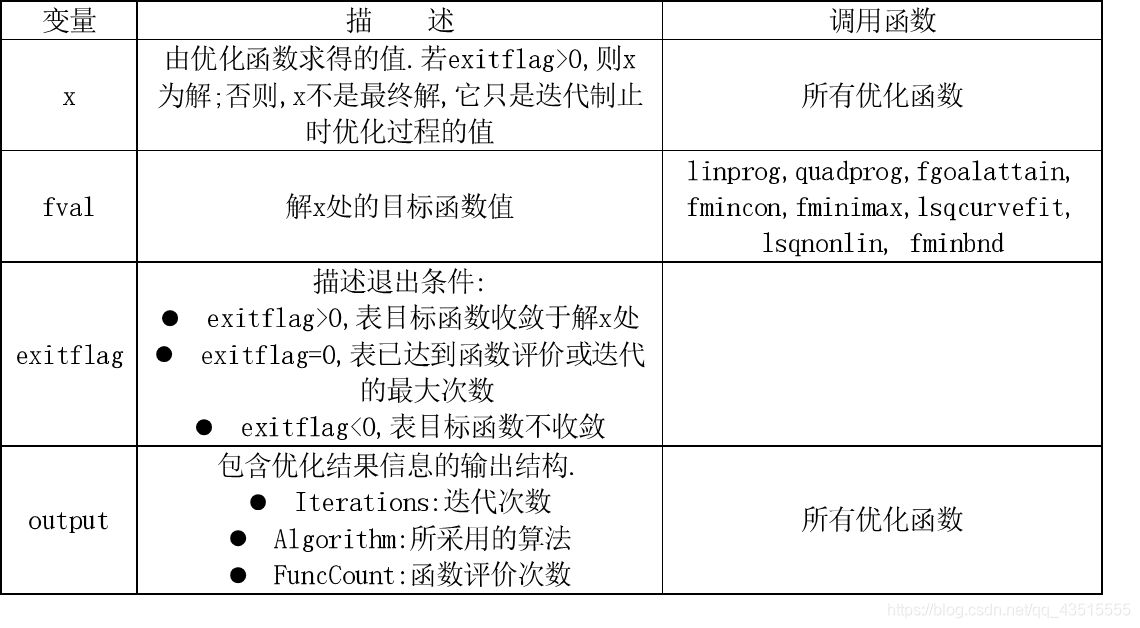
约束性优化问题

约束性优化问题是指除了给出方程外,方程的解还需要满足f（x）定义域约束等若干条约束条件,这种问题在实际生产中更有意义。约束条件分为等式约束与不等式约束。

说明：

[x,fv,ef.out,grad,hess]=fminunc(@f,x0,opt,P1,P2,…)
[x,fv,ef.out,]=fminsearch(@f,x0,opt,P1,P2,…)
[x,norm,res,ef,out,lam,jac]=lsqnonlin(@F,x0,v1,v2,opt,P1,P2,…)
[x,norm,res,ef,out,lam,jac]=lsqcurvefit(@F,x0,t,y,opt,P1,P2,…)

fminunc为无约束优化提供了大型优化和中型优化算法.由options中的参数LargeScale控制：
LargeScale=’on’(默认值),使用大型算法
LargeScale=’off’,使用中型算法
fminunc为中型优化算法的搜索方向提供了3种算法，由options中的参数HessUpdate控制：
HessUpdate=’bfgs’（默认值），拟牛顿法的BFGS公式；
HessUpdate=’dfp’，拟牛顿法的DFP公式；
HessUpdate=’steepdesc’，最速下降法
fminunc为中型优化算法的步长一维搜索提供了两种算法，由options中参数LineSearchType控制：
LineSearchType=’quadcubic’(缺省值)，混合的二次和三 次多项式插值；
LineSearchType=’cubicpoly’，三次多项式插

搜索步长的算法选择（lsqnonlin，lsqcurvefit）
LevenbergMarquardt = ‘off’ (GN法)
LevenbergMarquardt = ‘on’ (LM法，缺省值)
废话不多说，看具体的例子：

例1：

求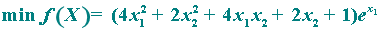
1、编写M-文件 fun1.m:

 function f = fun1 (x)
    f = exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
 

2、输入M文件myprg3.m如下:

  x0 = [-1, 1];
       x=fminunc('fun1',x0)
       y=fun1(x)

结果：

x =

    0.5000   -1.0000


y =

   3.6609e-16

求多变量函数的极小值点
customFunc.m

function [result] = customFunc(x,y,r,x1) 
%这里只有x1是函数变量，其他的都是从主函数中传递过来的参数。
result = sum(((x-x1(1)).^2+(y-x1(2)).^2).^(1/2).*r);
end

使用：Utitled3.m

x=[0,8.2,0.5,5.7,0.77,2.87,4.43,2.58,0.72,9.76,3.19,5.55];
y=[0,0.5,4.9,5,6.49,8.76,3.26,9.32,9.96,3.16,7.2,7.88];
r=[600,1000,800,1400,1200,700,600,800,1000,1200,1000,1100];

options=optimoptions('fminunc','Algorithm','quasi-newton','Display','iter');
f=@(x1) customFunc(x,y,r,x1);
[x,fval]=fminunc(f,[0,0],options);%初值必不可少，它告诉了fminunc函数你这个优化是几维的。

备注：
万能函数：fminunc
1）自定义的函数写在一个文件里面，可以是任意的函数，也允许携带参数。
2）重点是把函数封装到句柄里面，这样既可以给函数传递参数，也可以指明变量
3）最坑的地方是你自定义的函数中，作为函数变量的只能有一个！！！！如果是多元函数的话，那么这个变量是一个向量！！！比如函数变量为x1,如果是二元函数的话，你需要用x1(1)和x1(2)来调用函数变量

参考资料来源