数学实验第二课：函数迭代

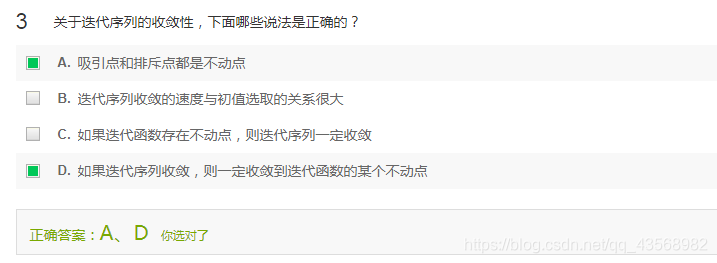
迭代

定理

在迭代函数连续的条件下，如果迭代序列收敛，则一定收敛于方程x=f(x)的根x*，这个根为函数的不动点。
不动点处的一阶导数小于1，则称不动点x为稳定的，若一阶导数等于0，则称不动点为超稳定，在超稳定附近，迭代过程x(n+1)=f(x(n))收敛到x*是非常快的。

用迭代法近似计算

计算三次根号2
过程分析
首先取
f(x)=2/x^2
因为f(2^(1/3))=2^(1/3)
在该点的导数=2>1,不满足要求

>> syms x;
>> y=diff(2/x^2);
>> subs(y,x,2^(1/3))%用值代替x
>> z=subs(y,x,2^(1/3));
>> fprintf('z = %.2f\n',z)%保留两位小数
z = -2.00

对上式恒等变形
x³=2
x³+ax²+bx=ax²+bx+2
x=(ax²+bx+2)/(x²+ax+b)
取f(x)=(ax²+bx+2)/(x²+ax+b)
令a=0,b=1,得f(x)=(x+2)/(x²+1)

对新的方程求解

>> syms x;
>> y=(x+2)/(x^2+1);
>> p=diff(y);
>> subs(p,x,2^(1/3))
>> z=subs(p,x,2^(1/3))
>> fprintf('z = %.2f\n',z)
z = -0.84

但这样收敛速度有点慢

继续变形
令a=0,b=4,得f(x)=(4x+2)/(x²+4),
f(x)=(ax+b)/(cx+d)
要满足a=d,b=3c

>> y=(4*x+2)/(x^2+4);
p=diff(y);
z=subs(p,x,2^(1/3)); fprintf('z = %.2f\n',z)
z = 0.15

>> f=inline('(4*x+2)/(x^2+4)');
>> x0=12;%初值随便给一个
>> for i =1:100
x0=f(x0);
fprintf('%g,%g\n',i,x0);
end
1,0.337838
2,0.814595
3,1.12754
4,1.23501
5,1.25606
6,1.25935
7,1.25984
8,1.25991
9,1.25992
10,1.25992
11,1.25992
12,1.25992
13,1.25992
14,1.25992

迭代上式，稳定在1.25992，即为其方程的解，即三次根号2的值为1.25992

验算logistics的收敛性
例如f(x)=ax(1-x),(0<=x<=1),a=3.2,x0=0.2
先编写一个Demo函数

function Demo(f,x0,N)
close all
for i =1:N
    axis([50,N,0,1]);
    if i>50
        plot(i,f(x0),'.');
        hold on ;pause(0.05);%画图加延迟
    end 
    x0=f(x0);
end;
hold off
clear all;

命令行下敲入

Demo(@(x)3.2*x*(1-x),0.2,200)

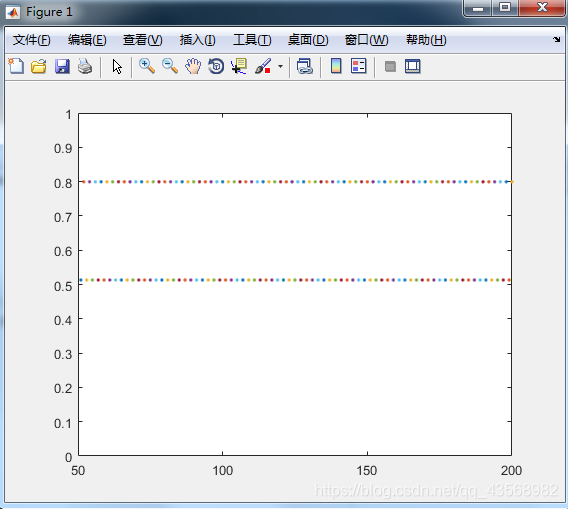
可以看出形成了循环，值一直在两个值上跳动，周期为2

更改a的值，可以出现不同的收敛情况
a=3.6,x0=0.6

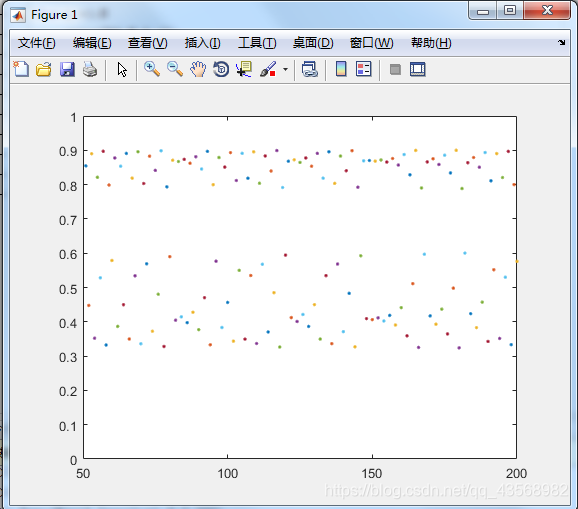
出现混沌现象

logistics模型

f(x)=ax(1-x) (0<=x<=1)
a>0，为logistics参数

在logistic函数中，首先取a的值为3，在（0，1）中随机取一数x。作为初值，进行迭代，共迭代300次左右，丢弃起始的100次迭代的数据，在图上绘出所有的点（a，Xn）（>100）.然后慢慢地增加a值，每增加一次，都重复前面的步骤，一直增加到a=4为止，画出最后所得到的图形。

logistic=inline('u*x*(1-x)');
for u=3.0:0.01:4
x0=rand;
for i =1:300
x0=logistic(u,x0);
if i>100
plot(u,x0,'k','linewidth',1);
hold on;
end;
end;
end;
hold off

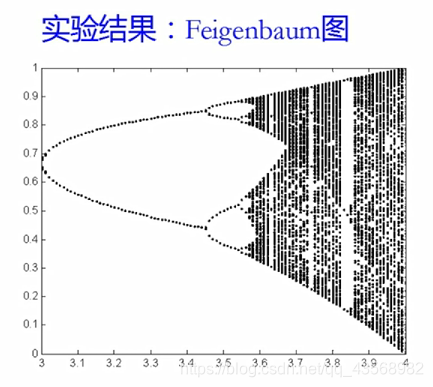
形成了周期的循环
画平行于y轴的直线

初值影响很大，所以叫做蝴蝶效应

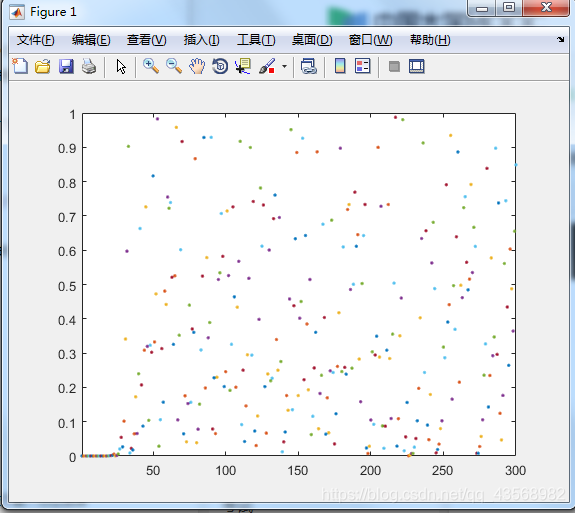
close all;clear all;
f=inline('3.99*x*(1-x)');
N=300;x0_1=0.663489000;x0_2=0.663489001;
for i=1:N
axis([1,N,0,1]);
yn=abs(f(x0_1)-f(x0_2));%取两个初值函数差的绝对值
plot(i,yn,'.');
hold on;pause(0.005);
x0_1=f(x0_1);
x0_2=f(x0_2);
end;
hold off;

迭代初期，差距不大，但是后面产生混沌现象，导致结果差距很大，蝴蝶效应

周期为2，可以取Feigenbaum上的值找周期

二维迭代

f=@(x,y)y-sin(x);
g=@(x)3.1-x;
xn=1.2;
yn=0;
for n=1:1000
xN=xn;
yN=yn;
xn=f(xN,yN);
yn=g(xN);
plot(xn,yn,'k*');
axis([-4,6,-3,7]);
pause(0.1);
hold on;
end
hold off

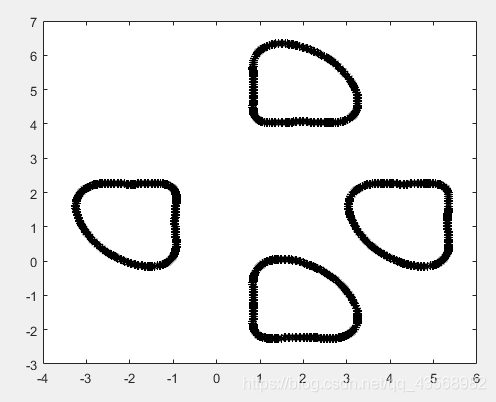
小图形经过旋转、折叠后可以重合，这类图形是分形图

Martin迭代

function Martin(a,b,c,N)%N为迭代次数
f=@(x,y)(y-sign(x)*sqrt(abs(b*x-c)));%f和g称为Martin迭代
g=@(x)(a-x);
m=[0;0];
for n=1:N
    m(:,n+1)=[f(m(1,n),m(2,n)),g(m(1,n))];
end
plot(m(1,:),m(2,:),'kx');
axis equal

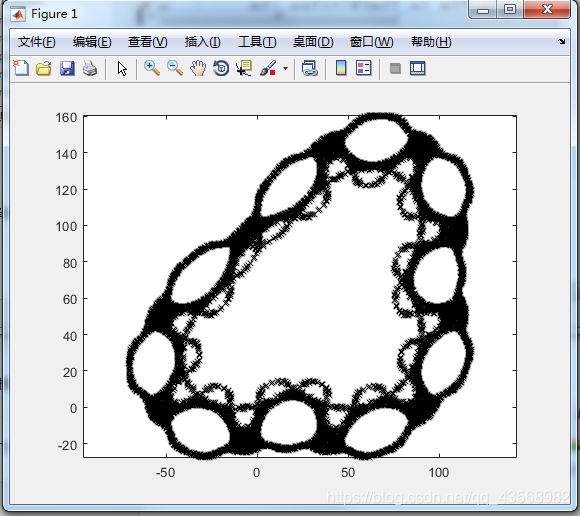
局部与整体具有某种相似
但不能从二维迭代散点图中判断迭代序列是否收敛