KM算法理解篇

文字内容出自：https://www.cnblogs.com/logosG/p/logos.html

一、匈牙利算法

匈牙利算法用于解决什么问题？
匈牙利算法用于解决二分图的最大匹配问题。
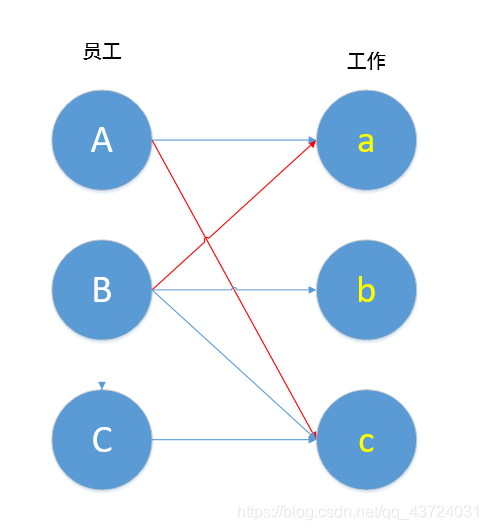
什么是二分图？我们不妨来考虑这样一个问题，在一家公司里，有员工A，B，C，有三种工作a，b，c，如果员工和工作之间有线相连，则表示员工能胜任这份工作。

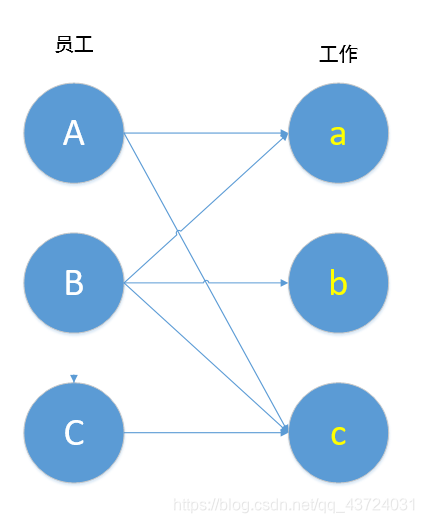
如图所示，员工发A能胜任a，c工作，员工B能胜任a,b,c工作，而员工c只能胜任c工作。
上图就是所谓的“二分图”（请忽略图中箭头），简单的说，上图可划分为两个集合{员工}，{工作}，两个集合之间的元素可以相连，同一集合内的元素不能相连。
下面请解决这样一个问题：请给出一个方案，让尽可能多的员工右不同的工作做。“匈牙利算法”的出现就是为了解决这个问题。
下面给出这个问题的解决方案：（读者看到这里可能会想，解决这个问题不是很简单吗？A→a,B→b，C→c不就好了？请注意：任何算法的给出都是为了规整化一个问题的解决步骤，其目的是为了在问题规模越来越大时算法对其仍然适用，如果公司有10个员工或者更多，读者想必不能一眼看出答案，此时，算法的作用便体现出来了。）
我们先帮A找工作做，不妨先帮A连上a（红线表示此时两者已经匹配），表示A去做a工作。

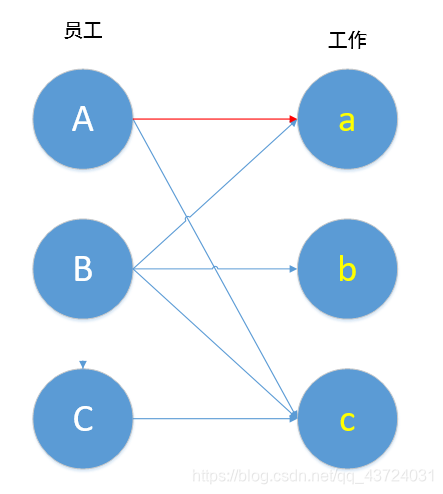
接下来我们帮B去找工作做，B的第一条线跟a相连，B也先做工作a。

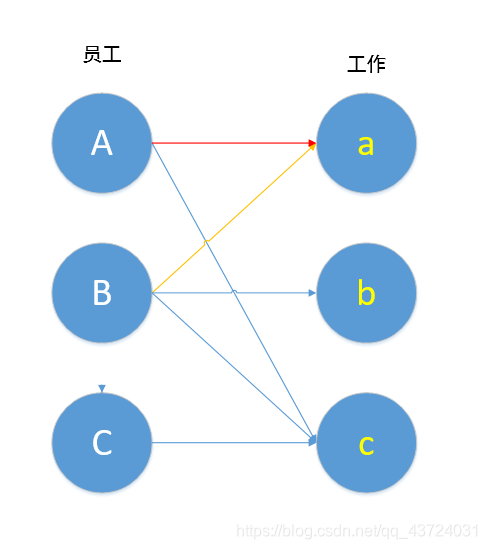
这时就发生了冲突，如何解决呢？
“匈牙利算法”指出：通过一条增广路径，通过取反操作，我们就能匹配更多的点。
什么时增广路径？增广路径是指，由一个未匹配的顶点开始，经过若干个匹配顶点，最后到达对面集合的一个未匹配项点的路径，即这条路径将两个不同集合的两个未匹配顶点通过一系列匹配顶点相连。
比如此题中，B 想做工作 a，于是 A 想着换一个工作，我们连上 A，c。

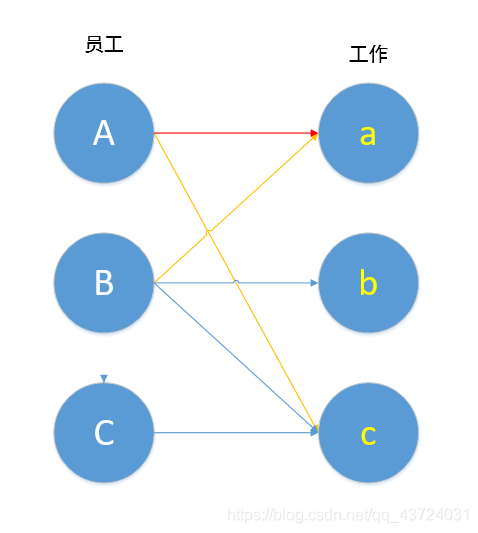
如图，B->a->A->c，其中B，c未匹配，A，a已匹配，按照定义，这就是一条增广路径，我们将其进行取反操作，就变成了下图。

取反操作为我们带来了什么？原本只有一条边匹配，现在有两边匹配，而且冲突也解决了，这就是匈牙利算法的妙处，我们能通过不停地寻找这样一条增广路径，从而找到二分图的最大匹配。
下面我们继续寻找增广路径。

最终，我们找到了一个最大图匹配：A 匹配 a，B匹配 b，C 匹配 c，就算集合中元素很多很多，我们仍能通过匈牙利算法得到该二分图的最大匹配。

int G[maxn][maxn],mh[maxn];
bool vis[maxn];
int m,n;	// m代表图左边一列，n代表图右边一列
bool dfs(int x)
{
    for(int y=1;y<=n;y++){
        if(G[x][y]==0) continue;
        if(!vis[y]){
            vis[y] = true;
            if(!mh[y]||dfs(mh[y])){
                mh[y] = x;
                return true;
            }
        }
    }
    return false;
}

int ans = 0;
for(int i=1;i<=m;i++){
	memset(vis,false,sizeof(vis));
	if(dfs(i))  ans++;
}

二、KM算法

现在我们来考虑另一个问题：如果每个员工做没见工作的效率各不相同，我们如何让得到一个最优匹配使得整个公司的工作效率最大呢？

这种问题被称为带权二分图的最有匹配问题，可由 KM 算法解决。
比如上图，A 做工作 a 的效率为 3，做工作 c 的效率为 4……以此类推。

1. 首先对每个点赋值，将左边的顶点赋值为最大权值，右边的顶点赋值为0。
   如图，我们将顶点 A 赋值为其两边中较大的 4。
   
2. 进行匹配，我们匹配的原则时：智育权重相同的边匹配，若找不到边匹配，对此路径的所有左边顶点 -1，右边顶点 +1，再进行匹配，若匹配不到，重复 +1和-1操作。（这里看不懂可以跳过，直接看下面的操作，之后再回头来看这里。）
   对 A 进行匹配，符合匹配条件的边只有 Ac 边。
   匹配成功！
   
   接下来我们对B进行匹配，顶点 B 值为3，Bc 边权重为3，匹配成~ 等等，A 已经匹配 c 了，发生了冲突，怎么办？我们这时候第一时间应该想到的是，让 B 换个工作，但根据匹配原则，只有 Bc 边 3+0=0 满足要求，于是 B 不能换边了，那 A 能不能换边呢？对 A 来说，也是只有 Ac 边满足 4+0=4 的要求，于是 A 也不能换边，走投无路了，怎么办？
   
   从常识的角度思考：其实我们寻找最优匹配的过程，也就是帮每个员工找到他们工作效率最高的工作，但是，有些工作会冲突，比如现在，B 员工和 A 员工工作 c 的效率都是最高，这时我们应该让 A 或者 B 换一份工作，但是这时候换工作的话我们只能换到降低总体效率值的工作，也就是说，如果令 R=左边顶点所有值相加，若发生了冲突，则最终工作效率一定小于 R，但是，我们现在只要求最优匹配，所以，如果 A 换一份工作降低的工作效率比较少的话，我们是能接受的（对 B 同样如此）。
   在KM算法中如何体现呢？
   现在参与到这个冲突的顶点是 A，B 和 c，令所有左边顶点值 -1，右边顶点值 +1，即 A-1,B-1. c+1，结果如下图所示。

我们进行了上述操作后会发现，若是左边有 n 个顶点参与运算，则右边就有 n-1 个顶点参与运算，整体效率值下降了 1*（n-（n-1））=1，而对于 A 来说，Ac 本来为可匹配的边，现在仍为可匹配边（3+1=4），对于 B 来说，Bc 本来为可匹配的边，现在仍为可匹配的边（2+1=3），我们通过上述操作，为 A 增加了一条可匹配的边 Aa，为 B 增加了一条可匹配的边 Ba。

现在我们再来匹配，对 B 来说，Ba 边 2+0=2，满足条件，所以 B 换边，a 现在为未匹配状态，Ba 匹配！

我们现在匹配最后一条边 C，Cc：5+1！=5，C 边无边能匹配，所以 C-1
现在 Cc 边 4+1=5，可以匹配，但是 c 已匹配了，发生冲突，C 此时不能换边，于是便去找 A，对于 A 来说，Aa 此时也为可匹配边，但是 a 已匹配，A 又去找 B。

B 现在无边可以匹配了，2+0 != 1 ，现在的路径是 C→c→A→a→B，所以 A-1，B-1，C-1，a+1，c+1。如下图所示。

对于 B 来说，现在Bb：1+0=1 可匹配！

使用匈牙利算法，对此条路径上的边取反。

如图，便完成了此题的最优匹配。

读者可以发现，这题中冲突一共发生了3次，所以我们一共降低了3次效率值，但是我们每次降低的效率值都是最少的，所以我们完成的仍然是最优匹配！

这就是KM算法的整个过程，整体思路就是：每次都帮一个顶点匹配最大权重边，利用匈牙利算法完成最大匹配，最终我们完成的就是最优匹配！

//原文大佬不匹配时-1和+1，这里时-slack和+slack
const int maxn = 1100;
const int INF = 0x3f3f3f3f;
int match[maxn],lx[maxn],ly[maxn],slack[maxn];
int G[maxn][maxn];
bool visx[maxn],visy[maxn];
int nx,ny;
bool findpath(int x)
{
    int tmp;
    visx[x] = true;
    for(int y=0;y<ny;y++){
        if(visy[y]) continue;
        tmp = lx[x] + ly[y] - G[x][y];
        if(tmp==0){
            visy[y] = true;
            if(match[y]==-1||findpath(match[y])){
                match[y] = x;
                return true;
            }
        }
        else if(slack[y]>tmp)
            slack[y] = tmp;
    }
    return false;
}
void KM()
{
    for(int x=0;x<nx;x++){
        for(int j=0;j<ny;j++) slack[j] = INF;
        while(true){
            memset(visx,false,sizeof(visx));
            memset(visy,false,sizeof(visy));
            if(findpath(x)) break;
            else{
                int delta = INF;
                for(int j=0;j<ny;j++){
                    if(!visy[j]&&delta>slack[j]){
                        delta = slack[j];
                    }
                }
                for(int i=0;i<nx;i++){
                    if(visx[i]) lx[i] -= delta;
                }
                for(int j=0;j<ny;j++){
                    if(visy[j]) ly[j] += delta;
                    else    slack[j] -= delta;
                }
            }
        }
    }
}
void solve()
{
   memset(match,-1,sizeof(match));
   memset(ly,0,sizeof(ly));
   for(int i=0;i<nx;i++){
        lx[i] = -INF;
        for(int j=0;j<ny;j++){
            if(lx[i] < G[i][j]){
                lx[i] = G[i][j];
            }
        }
   }
   KM();
}