Comet OJ - Contest #15 当我们同心在一起

传送门：https://cometoj.com/contest/79/problem/B
题目描述

平面上有 n 个坐标相异的点，请问当中有多少组非共线的三个点，这三个点的外心也在这 n 个点之中？

输入描述

第一行有一个正整数 n 代表平面上的点数。
接下来有 n 行，当中的第 i 行包含两个整数 x_i, y_i​ ，代表第 i 个点的坐标是 (x_i， y_i)。
  1 <= n <= 2000
  10⁹ <= x_i，y_i <= 10⁹
  若 i != j，则(x_i,y_i) != (x_j,y_j)

输出描述

输出一个整数代表答案。

样例1输入：

5
0 0
-2 0
0 2
-1 1
2 0

样例1输出：

2

样例1解释：

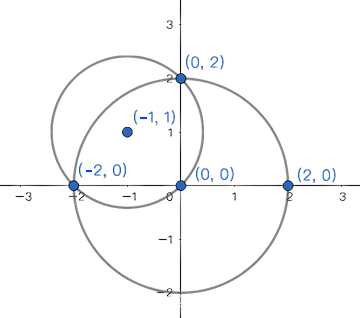
此样例的示意图如下：

  刚开始做这个题目的时候，没想太多，map标记所有点，遍历所有组合，求外心，然后找一下外心的坐标是不是在map里。
  然而，这样时间复杂度不被允许，一直TL，一直爽。
  仔细想一下，外心到圆上的点的距离距离相同，也就是说这三个点的外心到这三个点的距离相同；那样我们可以记录所有点的距离，以及距离出现的次数，假设距离 d 出现的次数是 x，那么 x*(x-1)*(x-2)/6（从 x 个里取 3 个）就是该距离下的组合数目。
  我们可以用 map 记录距离出现的次数，然后用遍历 map 就行了，当然也可以用哈希map，但是 map 没 TL，就用 map 了。

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
#include<ctime>
#include<utility>
#include<map>
#define ll long long
#define ld long double
#define ull unsigned long long
using namespace std;
const int INF = 0x3f3f3f3f3f;
const double eps = 1e-6;
const int maxn = 10010;
pair<int,int> p[maxn];
#define x first
#define y second

int main(void)
{
    int n;
    ll ans = 0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&p[i].x,&p[i].y);
    for(int i=1;i<=n;i++){
        map<ll,ll> mp;
        for(int j=1;j<=n;j++){
            if(i==j)    continue;
            ll dy = p[i].y - p[j].y;
            ll dx = p[i].x - p[j].x;
            ll d = dx*dx + dy*dy;
            mp[d]++;
        }
        map<ll,ll>::iterator it = mp.begin();
        while(it!=mp.end()){
            ll c = it->second;
            ans += c*(c-1)*(c-2)/6;
            it++;
        }
    }
    printf("%lld\n",ans);
    return 0;
}