汉诺塔递归问题

作者：半只鸡加薯条
链接：https://www.zhihu.com/question/24385418/answer/86797711
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

这个问题最近挺困扰我，网上看了很多文章都在说用函数的角度去理解整个过程，确实是没错而且是一种聪明的办法，但是有强迫症的我还是花了些时间去思考了一下递归每一步的运行，说一下个人的理解吧。 如有不正确以及不完善的，还请前辈指正。首先贴上汉诺塔程序java代码假设三个柱子分别为a，b，c。hanoi(n,a,b,c)表示把n个盘子从a转移到c。1.当只有一个盘子时，很简单，把它从a直接移动到c，也就是执行了n1的情况。记该动作为move（a，c）,代码中直接使用打印输出表示该动作。 2.当有两个盘子时，即调用方法hanoi(2,a,b,c)，理解为把2个盘子从a移动到c。分为3个步骤。 i.首先把最上面的盘子移动到b ii.把下面的盘子移动到c iii.把b的盘子移动到c。 为了便于理解递归，我们使用n1时的动作，只是把柱子的编号进行一些变化。对于步骤i，动作为move(a,b)，相当于调用方法hanoi(1,a,c,b),即交换b柱和c柱的编号，此时打印输出a->b;对于步骤ii，不对自身进行调用，因为始终是由a至c，因此直接打印输出a->c；对于步骤iii，动作为move(b,c),相当于调用hanoi(1,b,a,c),即交换a柱和b柱编号。因此对于2个盘子的情况，递归算法可以写为 hanoi(1,A,C,B); System.out.println(A+"->"+C); hanoi(1,B,A,C); 3.同样对于3个盘子的情况，将上面两个盘子视为一个大盘子，第一步将该大盘子转移到b，相当于调用hanoi(2,a,c,b)，即把两个盘子从a移动到b。第二步将a上的最下面的盘子移动到c，执行注释2对应的语句；最后，把b上的两个盘子转移到c,即调用hanoi(2,b,a,c)。因此对于三个盘子的代码可以写为 hanoi(2,A,C,B); System.out.println(A+"->"+C); hanoi(2,B,A,C); 由以上就很容易推出n个盘子的情况了。对于代码的执行情况和基本思想是一样。分割线------------------感谢有同学提出我的回答的错误所在，在此回头看了一下，的确写的乱七八糟，就把之前写的删了。现在我自己画了一张图，虽然有点丑，但是阐明了执行顺序和过程。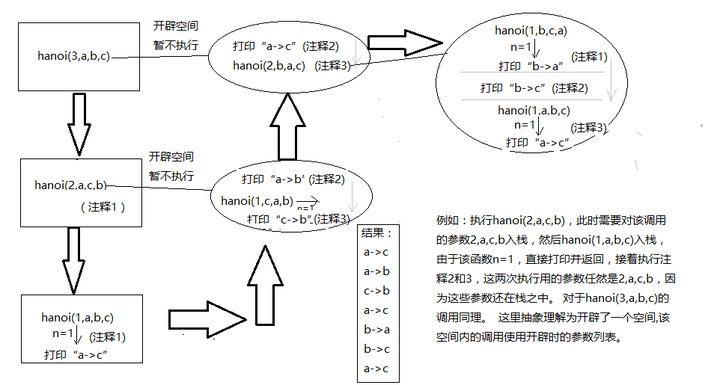箭头表示实际的代码语句执行顺序。每一次调用hanoi()时，都会首先判断n的值，若不为1，将当前参数入栈并将接下来的调用入栈，里面的函数返回后出栈继续执行接下来的语句，这一点在图片中的举例有详细说明。不懂的可以查一下函数调用过程其实就是栈的操作，对于理解递归很有用。虽然在使用递归时并不需要纠结在这些细节，只需要将功能视作函数操作就行，但是还是希望能有助于理解，毕竟熟练运用递归并非易事。第一次写这方面的内容，如果有分析的错误还请指正。
C语言代码

#include <stdio.h>
int main()
{
    int hanoi(int,char,char,char);
    int n,counter;
    printf("Input the number of diskes：");
    scanf("%d",&n);
    printf("\n");
    counter=hanoi(n,'A','B','C');
    return 0;
}

int hanoi(int n,char x,char y,char z)
{
    int move(char,int,char);
    if(n==1)
        move(x,1,z);
    else
    {
        hanoi(n-1,x,z,y);
        move(x,n,z);
        hanoi(n-1,y,x,z);
    }
    return 0;
}

int move(char getone,int n,char putone)
{
    static int k=1;
    printf("%2d:%3d # %c---%c\n",k,n,getone,putone);
    if(k++%3==0)
        printf("\n");
    return 0;
}

`