解耦:寻找合适的控制规律,使输入输出相互关联的多变量系统实现每一个输出仅受相应的一个输入的控制,每个输入也仅能控制一个输出。(动态解耦方法和静态解耦方法)
1、动态解耦
寻找一个输入变换和状态反馈矩阵,使导出的闭环系统传递函数矩阵为对角矩阵
传递函数矩阵:
基于状态空间的结构特征指数和结构特征向量:
结构特征指数:
而
或者
结构特征向量:
基于传递函数的结构特征指数和结构特征向量
分母多项式次数-
分子多项式次数
结构特征指数:
结构特征向量:
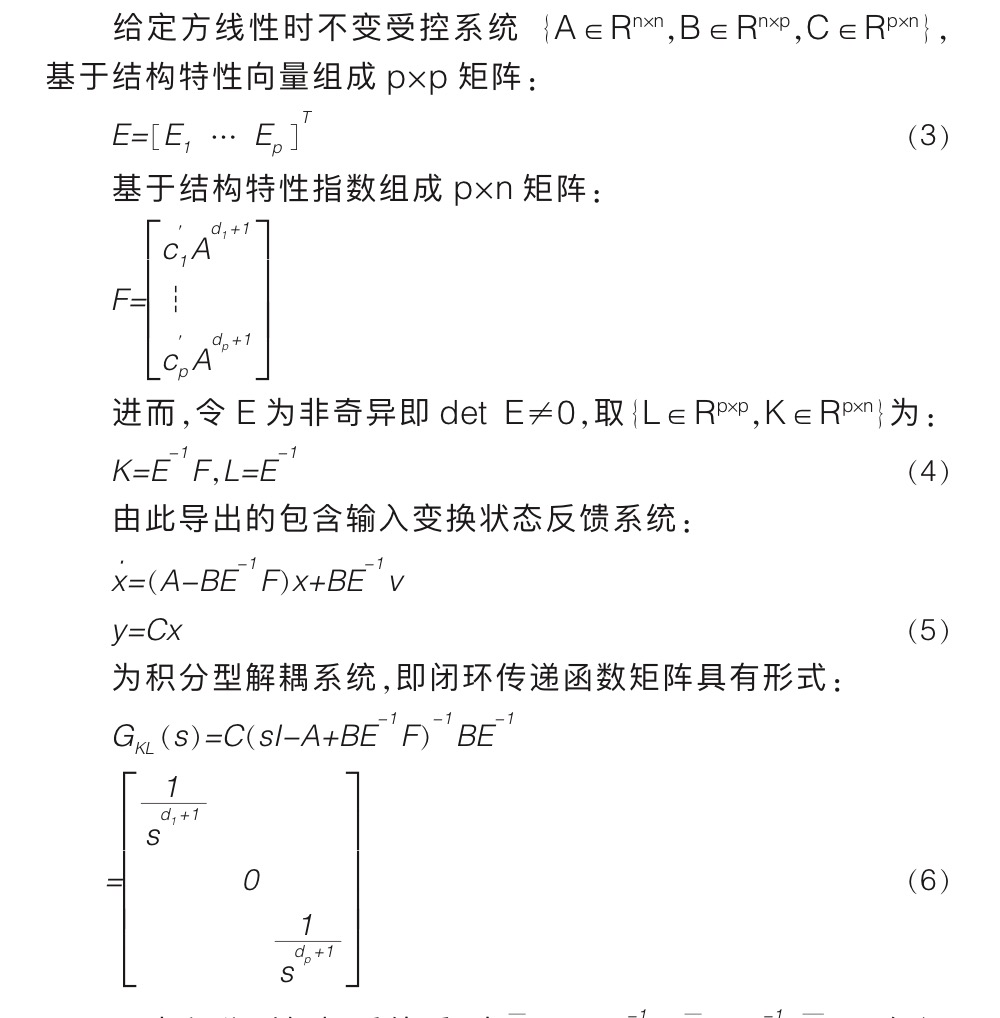

怎么求解耦规范型??????

解耦:寻找合适的控制规律,使输入输出相互关联的多变量系统实现每一个输出仅受相应的一个输入的控制,每个输入也仅能控制一个输出。(动态解耦方法和静态解耦方法)
1、动态解耦
寻找一个输入变换和状态反馈矩阵,使导出的闭环系统传递函数矩阵为对角矩阵
传递函数矩阵:
基于状态空间的结构特征指数和结构特征向量:
结构特征指数:
而
或者
结构特征向量:
基于传递函数的结构特征指数和结构特征向量
分母多项式次数-
分子多项式次数
结构特征指数:
结构特征向量:


怎么求解耦规范型??????

 1461
1461

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


