电子的路(电路基础笔记)

创世章

电流传

---

$$I\stackrel{\Delta }{=}\underset{\Delta \to 0}{\lim }\frac{\Delta q}{\Delta t}=\frac{dq}{dt}$$

电压传

---

要说起电压，我们便先来瞧瞧电场。

电场者

---

$$E=\frac{F}{q}$$

电场力做功

---

运用微分，将电场力做功细分为一小段一小段的恒力做功。
$$\begin{array}{rl}\sum _{i=1}^n\Delta x_i=x_{ab},W_{ab}& =\underset{n\to \infty }{\lim }\sum _{i=1}^{n}F(x)\Delta x_i\\ & =\underset{n\to \infty }{\lim }\sum _{i=1}^{n}qE(x)\Delta x\\ & =q{\int }_{x_a}^{x_b}E(x)dx\end{array}$$

---

上面的定义是我还不知道有线积分的时候写出来的，只考虑了一维的情况，更完善的表述如下
$$W={\int }_{L}q\vec{E}\cdot \mathrm{d}\vec{x}$$

电压登场

---

$$U_{ab}\stackrel{\Delta }{=}\frac{\partial W_{ab}}{\partial q}={\int }_{x_a}^{x_b}E(x)dx$$
可见，当 $q=1,u_{ab}=W_{ab}$， 所以我们也可以定义
$$电压等于单位电荷从a到b电场力所做的功。$$

磁链传

---

$$\psi (t)={\int }_{-\infty }^{t}u(\tau )d\tau$$
所以$$u(t)=\frac{d\psi }{dt}$$
可见，电压大小等于磁链（磁通量）。

电功率传

---

$$P=\frac{dw}{dt}=\frac{Udq}{dt}=UI$$
若电流的实际方向和电压的实际方向相同，P就是正的。

此时正电荷从电势高的地方跑到电势低的地方，电场力做正功，也就是电流做正功，这个功用来驱动电路元件，所以此时的功率我们可以认为是电路元件吸收或者消耗的功率。

一窥究竟

---

从上面看，其实我们可以认为电流 $I$ 与 $U$ 其实联系不大。

实际方向

---

电流

正电荷运动的方向

电压

电压降的方向

参考方向

---

确定好参考方向，便于 数值计算 并方便地解释 正负号的意义。

我觉得关注单独的某个元件的某个物理量的参考方向没有太大作用。若要实现上述目的，就得搞清楚各个物理量参考方向之间的关系所带来的对正负号解释的影响。

注意，电路图中的标号就已经确定了电压和电流的参考方向。

若实际方向与参考方向相同，那么符号为＋，否则为－。

u, i 参考方向的关系

---

$$u,i参考方向一致：关联参考方向$$$$u,i参考方向不一致:非关联参考方向$$
 

带来的影响

---

欧姆定律是基于关联的

KCL：通常规定，若 $i_k$ 参考方向流出节点，前面取 $+$；若流入节点，前面取 $-$。这样规定是因为KCL说明了流入一个元件的电流等于流出该元件的电流，＋－号相当于把电流分为了流入和流出，这才是本质。

KVL：通常规定，若 $u_k$ 参考方向与回路方向（又一个参考方向）相同，前面取 $+$；若相反，前面取 $-$。这样规定是因为KVL说明了一个回路中沿一个方向的电压升降和为0。正负号把电压分为了电压升和电压降。

KCL KVL 总结

---

KVL与电位单值性等价。这个从 关联矩阵转置乘路径向量等于零 求回路的本质是一样的，因为形成回路每个节点一定既当首又当末。

另外KVL也能由麦克斯韦方程的第二个式子推出。

KCL本质是电荷守恒。

再讨论一下独立方程个数和有限解的情况。

---

电路元件

有源元件

这种接法是错误的，会产生矛盾。

---

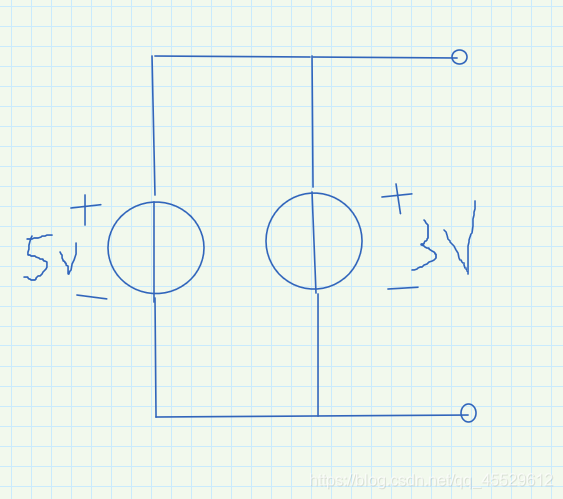
电压相同的地方可以捏成一个节点。

支路电路法

以 b 个支路电流为待求量，按 KCL、KVL 列 b 个独立方程。

若支路 k 为 电流源 $I_s$， 则支路电流 $I_k=I_s$ 是已知的，而电流源两端的电压是未知的，若不求 $U_k$ 则v不必对含电流源的支路列 KVL 方程。欲求 $U_k$ 则需列。

先找出 n 个节点，列 KCL，再列 KVL 补足方程个数。

节点电压法 Node Voltage Method

---

1. 确定参考节点;
2. 给节点处的电位值命名；
3. 求解简单节点（比如与电源相连的节点）；
4. 列 KCL 方程，并用电压表示电流（可用互导形式列方程）；
5. 求解方程组。

在这种求解方法中，KVL 自动成立，因为确定节点电压的同时就承认了电位单值分布，等价于KVL。

$$KVL\to 电压单值性\leftarrow 电位差表示支路电压$$

网孔电流法 Mesh Current Method

---

1. 确定每个网孔的环电流参考方向；
2. 求解简单的网孔电流（如电流源流出的电流）；
3. 列 KVL 方程， 并用电流表示电压（可用互阻形式列方程）；
4. 求解方程组。

让流过已知电流（如含电流源）的回路只有一个，这样该回路环电流就已知了，减少方程个数。

这个方法中的环电流不是实际存在的，它们经过叠加后的绝对值等于实际电流的大小。

因为回路电流表示电流的电流连续性，而KCL也表述了电流连续性，因此以回路电流为待求量自动满足KCL。

$$KCL\to 电流连续性\leftarrow 回路电流表示支路电流$$

---

定理合集

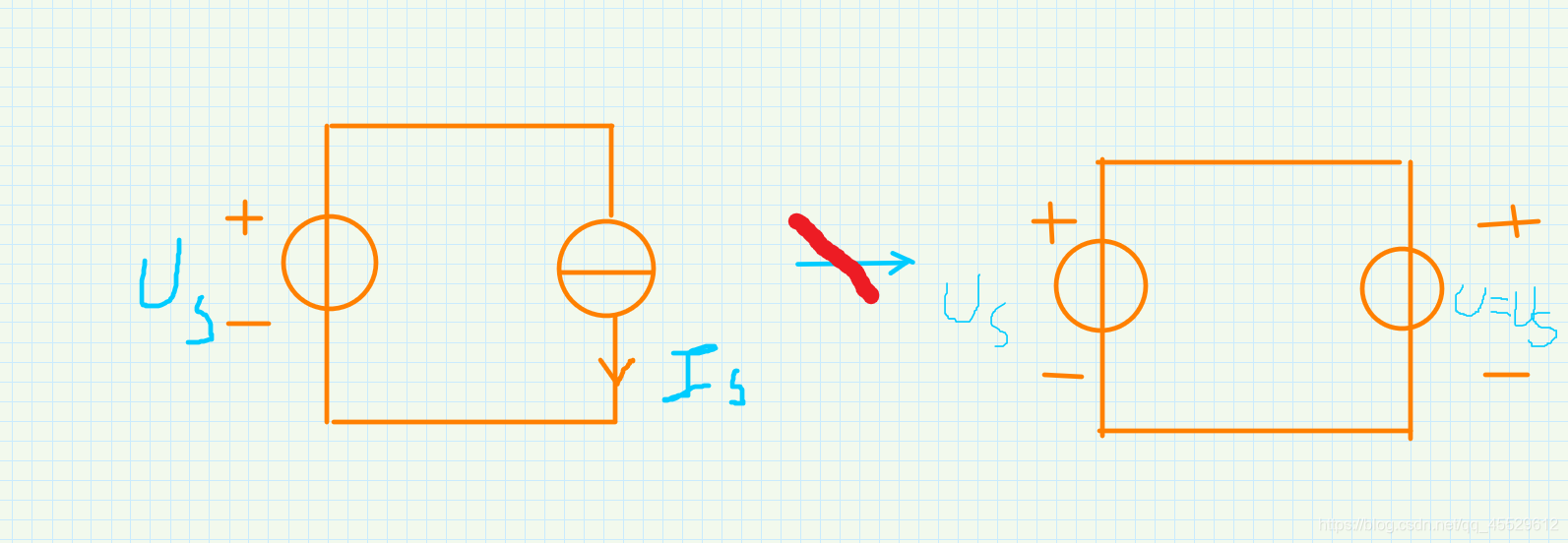
置换定理

若一端口 $N$ 的电压为 $U$ 或者电流为 $I$，则可用 $U_s=U$ 或 $I_s=I$ 的电源来置换一端口 $N$，置换后剩余部分电路的电压电流保持不变。

原理：置换前后所列的方程一样。

使用条件：

1. 置换前后电路参数应保持不变。
2. 置换后的电路有唯一解。
   反例：置换后无法解出电路的电流，或者说电流的解有无穷多个。
   

齐性定理

线性直流电路的响应（$U$ 或 $I$）是 各独立源 $U_s、I_s$ 的一次齐性函数。若只有一个独立源，则响应与激励成正比。

推论：无（独立源）一端口电路可用输入电阻 $R_{in}$（或 $G_{in}$）等效替代。

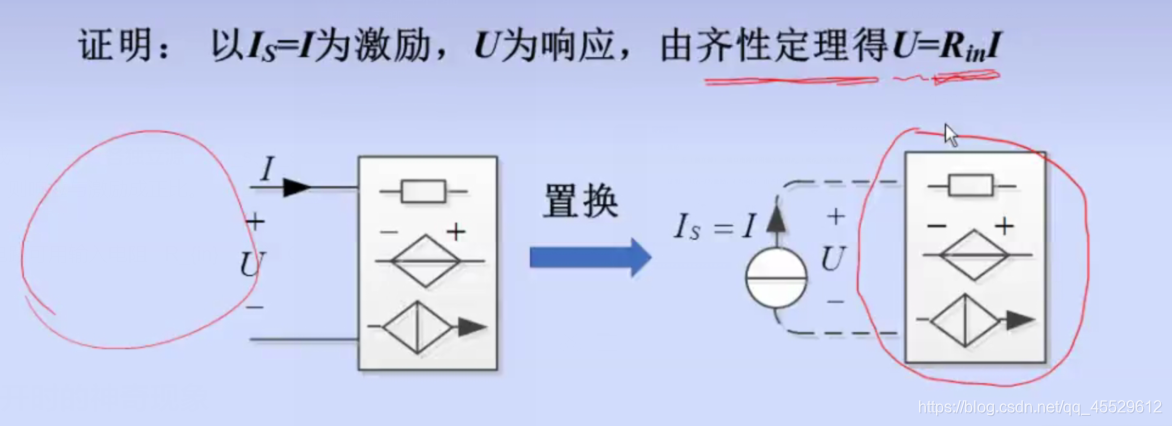
如果我们要求解这个等效的电阻 $R_{in}$，只需 $R_{in}=\frac{U}{I}$
 

叠加定理

定义

在线性电路中，几个独立源共同作用产生的响应等于各独立源单独作用时产生响应的代数和。

证明

其实从齐性定理中我们可以推出叠加定理。因为响应是各独立源的线性叠加，如果让一个独立源保持不变其余独立源全部置零（电压源用短路替代，电流源用断路替代，受控源要保留），这就等价于某个独立源单独作用于电路。

应用

各独立源分组作用。从另一个角度看，一个独立源也可以分解为等效的多个电源。（可以用于求解对应于某个电流源增大或减小的新响应：我们只需单独考虑增大或减小的那部分，计算带来的响应增量）

注意：1) 线性电路（要有唯一解）。
2） 代数叠加时注意参考方向。

等效电源定理

定义

等效电源定理是指我们能够将任何含源的 一端口 电路化简为戴维南电路 或 诺顿电路。所以等效电源定理包括戴维南定理和诺顿定理。
(图待添加)

证明

应用

1. 化简复杂线性一端口；
2. 线性抽象电路计算。

注意：

1. 适用范围：含源线性一端口，但端口外电路可以是非线性的；
2. 注意等效电源的方向；
3. 一般来说，两种等效电路同时存在，但
   ① 若 $R_{in}=0$，只有戴维南等效电路，成为电压源；
   ② 若 $G_{in}=0$，只有诺顿等效电路，成为电流源。

（相关图片待添加）

如果电路内部发生变化，则不能用同一个模型等效。

特勒根定理

互易定理

总结

对电阻等效化简，结合已知条件使用置换定理，对参数不变的电路部分进行电源等效。多个电源或者电源会变化则使用齐性定理和叠加定理。特勒根定理适用于求解两个结构相同的电路或者不同时间下的同个电路。

记住一些结论比如电桥平衡的性质、电阻分压等有利于直观地分析电路。

抽象电路考虑 齐性定理。如果元件布局和参数不变，那么独立源前面的系数也不会改变。

 

---

正弦稳态分析

相量法

假设一端口元件两端电压为
$$u=U_m\cos (\omega t+\phi )$$
那么我们可以把它添加一个特殊的虚部
$$u=U_m\cos (\omega t+\phi )+j{U}_m\sin (\omega t+\phi )$$
接下来就可以利用欧拉方程把电压从三角形式转化成复指数形式
$$U_m{e}^{j(\omega t+\phi )}=U_m{e}^{j\phi }{e}^{\omega t}$$
因为正弦稳态电路的 $\omega$ 是不变的，所以 $e^{\omega t}$ 也是保持不变的。所以 $U_m{e}^{j\phi }$ 包含了电压的全部信息，我们还可以把它写成相量形式
$$U_m\angle \phi$$
这样我们就可以把电压看成是复平面上的一个向量。

我们为什么要大费周章的把电压表示成这种形式呢？

这是因为转化成相量形式后，基尔霍夫定律有相同的形式；相量的加减其实就是复数的加减，等同于具有实际意义的实部的加减；此外最为重要的是 电压或电流对时间求导，在化成相量（本质是复指数）后求导变成了乘以一个复常数，把微分方程转化成了代数方程。

注意，被求量无关电功率的时候，电流和电压不会相乘（没有涉及相量或者说复数的乘法运算），只有电压电流的线性组合（数乘和加法运算）（系数现在已经拓展到了复数，这是电感电容动态导致的），电压电流都可写成 $A{e}^{j\phi }{e}^{\omega t}$，线性组合后总可以提出公因式 $e^{\omega t}$，方程两端的 $e^{\omega t}$ 也就消掉了。所以实际列基尔霍夫定律方程（及其一系列变形）我们都只需要关注 $A\angle \phi$ 的运算就可以了。这样，我们就得到 相量形式的基尔霍夫定律。

有效值本身不满足基尔霍夫定律，但有效值的相量形式 $U\angle \phi$ 满足基尔霍夫定律。这是因为 方程两边同除 $\sqrt{2}$仍然成立。

---

正弦电路功率

我一开始出现了一个疑惑，为什么 $ui$ 的运算写成相量形式后不等价于 $$U\angle {\phi }_u\cdot I\angle {\phi }_i=UI\angle ({\phi }_u-{\phi }_i)$$
而求非功率量时这个等式则成立？因为
$$ui=U{e}^{j{\phi }_u}{e}^{j\omega t}\cdot U{e}^{j{\phi }_i}{e}^{j\omega t}=UI{e}^{j({\phi }_u+{\phi }_i)}{e}^{j2\omega t}$$
这个$e^{j2\omega t}$ 并没有相关方程可以让它在两边消掉，所以我们不能只考虑前面那部分。

至于求非功率量时，为什么也会出现 $$A\angle \phi \cdot I\angle {\phi }_i=UI\angle ({\phi }_u-{\phi }_i)$$
其实这里的第一个量 $A\angle \phi$ 并不是相量，它其实是阻抗或导纳，只不过把它写成这种形式，复数部分来自电容和电感。$A\angle \phi =R+j(X_L-X_C)$，只是单纯的一个复数，不像电压电流这种实际上是 $U_m\angle \phi \cdot e^{j\omega t}$，所以不会引入 $e^{j2\omega t}$，基尔霍夫方程两端都只有 $e^{j\omega t}$，可以同除消掉。

正弦电路一端口瞬时功率

$$\begin{array}{rl}p& =\sqrt{2}U\cos (\omega t+{\psi }_u)\cdot \sqrt{2}Icos(\omega t+{\psi }_i)\\ & =UI\cos ({\psi }_u-{\psi }_i)+UI\cos (2\omega t+{\psi }_u+{\psi }_i)\end{array}$$

正弦电路一端口平均功率（有功功率）

$$\begin{array}{rl}P& =\frac{1}{T}{\int }_{T}p\mathrm{d}t\\ & =UI\cos ({\psi }_u-{\psi }_i)\\ & =UI\cos \phi =UI\lambda \end{array}$$
称 $\lambda$ 为功率因数，$\phi$ 为功率因数角

可见，电流和电压的相位差会影响有功功率。

无功功率

瞬时功率的幅值（$UI$）称为无功功率，用来衡量元件和外部电路交换能量的速率。

复功率

人为构造出的复数
$$\hat{S}=P+jQ=UI\cos \phi +jUI\sin \phi =UI\angle \phi =S\angle \phi$$
为什么我们要人为构造这么一个复数呢？

为的是方便用相量法直接计算 $P、Q、S$。复功率等于电压相量和电流相量共轭的乘积。
$$\hat{S}=S\angle \phi =S(\angle {\psi }_u-\angle {\psi }_i)=\stackrel{.}{U}\stackrel{\ast }{I}$$

若阻抗为 $Z=R+jK$，则 $\hat{S}=\stackrel{.}{U}\stackrel{\ast }{I}=Z\stackrel{.}{I}\stackrel{\ast }{I}=I^{2}Z=I^{2}R+j{I}^{2}K$

所以 $P=I^{2}R，Q=I^{2}K$

三表法测阻抗

4

复功率守恒

平均功率守恒，无功功率守恒。（电源发出和负载消耗的功率相同）

功率因数的提高

为何要提高？为了减小无功功率。传输相同的有功功率，如果电压固定，功率因数小的话则需要较大的电流，这样传输过程损耗增多，因而需要加粗导线，成本增加。

为什么不并联电阻呢？

问题

最大功率原理

1. 共轭匹配
2. 模匹配

注意我们在计算最大功率时，有一个大前提，电源内阻固定，而且计算的是外电路的最大功率。所以不能随便把负载放进内电路，这样会导致计算结果不是我们想要的。

互感

本质，两个或两个以上的线圈存在磁耦合现象。互感针对两个线圈存在磁耦合现象，也就是穿过一个线圈的磁链除了自身产生的磁链之外（自感应），还有旁边的线圈产生的磁链（互感应）（统称磁耦合现象）

$L$ 代表自感系数和互感系数，如果电流参考方向和磁链参考方向满足右手定律
${\psi }_1={\psi }_{11}\pm {\psi }_{12}=L_{11}{i}_1\pm L_{12}{i}_2$
${\psi }_2=\pm {\psi }_{21}+{\psi }_{22}=\pm L_{21}{i}_1+L_{22}{i}_2$

可以证明（虽然我没证明过~）$L_{12}=L_{21}=M$
$L_{11}、L_{22}$ 通常记为 $L_1、L_2$

所以我们可以得到
${\psi }_1=L_1{i}_1\pm M{i}_2$
${\psi }_2=\pm M{i}_1+L_2{i}_2$

同名端

当两个线圈电流激发的自感和互感磁链方向相同时，电流流入的两个端子称为同名端，用 * 标记。

所以 $L$ 前的正负号取决于电压电流的参考方向是否关联。$M$ 前的正负号既取决于电压电流的参考方向是否关联，也取决于电流流入端口是否为同名端。

互感元件的等效电路和去耦合等效

主要分为 串联、并联、一端相接 三种情况。其中，前二者是第三个的特殊情况。

对于第三种情况满足第二种情况推导出来的结果

耦合系数 $k=\frac{M}{\sqrt{L_1{L}_2}}\le 1$

含互感元件的正弦电流电路

使用 支路电流法 和 回路电流法。原因如下。

或者等效成 非耦合电感电路。

三相电路

电压、负载对称，那么利用对称性可以得知电流也是对称的。

星型对称三相电路：线电压是相电压的 $\sqrt{3}$ 倍。线电压是相应两条线相电压的差。

角形对称三相电路：电源部分，线电流是相电流的 $\sqrt{3}$ 倍。线电流是相应（同节点）相电流的差。电源端为非关联参考方向，负载端为关联参考方向。

对于角形负载，相电流参考方向一般是 $ABBCCA$.

$A^{\prime }、B^{\prime }$之间的电压为什么并不是380V？
解法是先化成星结。

有关三相电路，觉得最关键的是画出相量图，然后根据图直观地进行加减法。（注意如果要确切计算，就要先明确参考相量是哪个，或者某个相量的相位）

---

非正弦电路分析

应当选 B，相量对应特定频率，不同频率下的相量不能叠加。

注意，求非正弦电路中某个元件的平均功率时，直流分量直接相乘（不用除以 $\sqrt{2}$），而谐波分量则是有效值相乘，然后叠加。

谐振

谐振的数学本质是导纳的虚部为0，在物理上体现为 任何含有电感和电容的一端口网络的端口电压与电流同相位。

根据导纳虚部为0，我们可以求出 谐振角频率 ${\omega }_0=\frac{1}{\sqrt{LC}}$；

根据谐振角频率，我们可以求出特性阻抗 $\rho ={\omega }_{0}L=\frac{1}{{\omega }_{0}C}=\sqrt{\frac{L}{C}}$

再引入品质因数，品质因数的定义随谐振类型的不同而不同。为的是方便分析复杂电路中电容器或电感两端的电压（串联谐振）或电流（并联谐振）。

对于串联谐振，此时总阻抗最小，电流有效值最大。注意在 ${\omega }_0$ 处并不是电感电容两端电压的极大值。

---

小技巧：阻抗模 乘 电流有效值 等于 电压有效值。（可从相量形式的欧姆定律得到，两边取模即可）

---

电感电路开关断开时的神奇现象

---

我i们已知
$$u=\frac{\mathrm{d}i}{\mathrm{d}t}$$
当开关断开时，电流在极短时间内降低至 0 ，电流的变化率十分大，产生的电压也十分大，足以击穿空气产生火花。

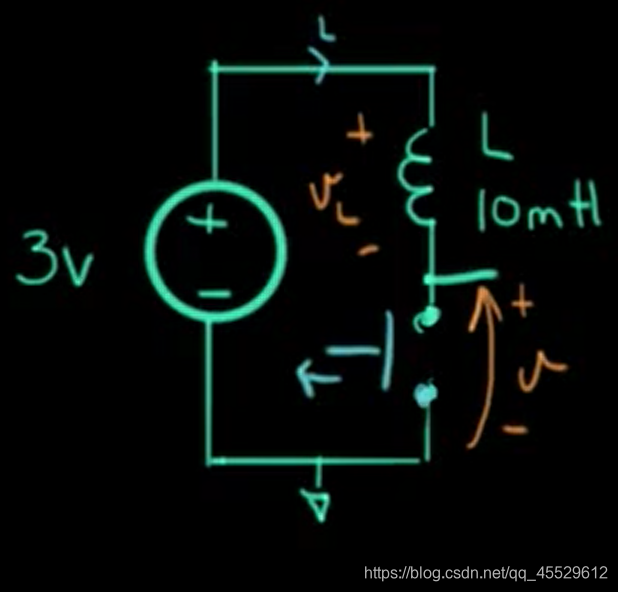
解决方法

---

电感反冲

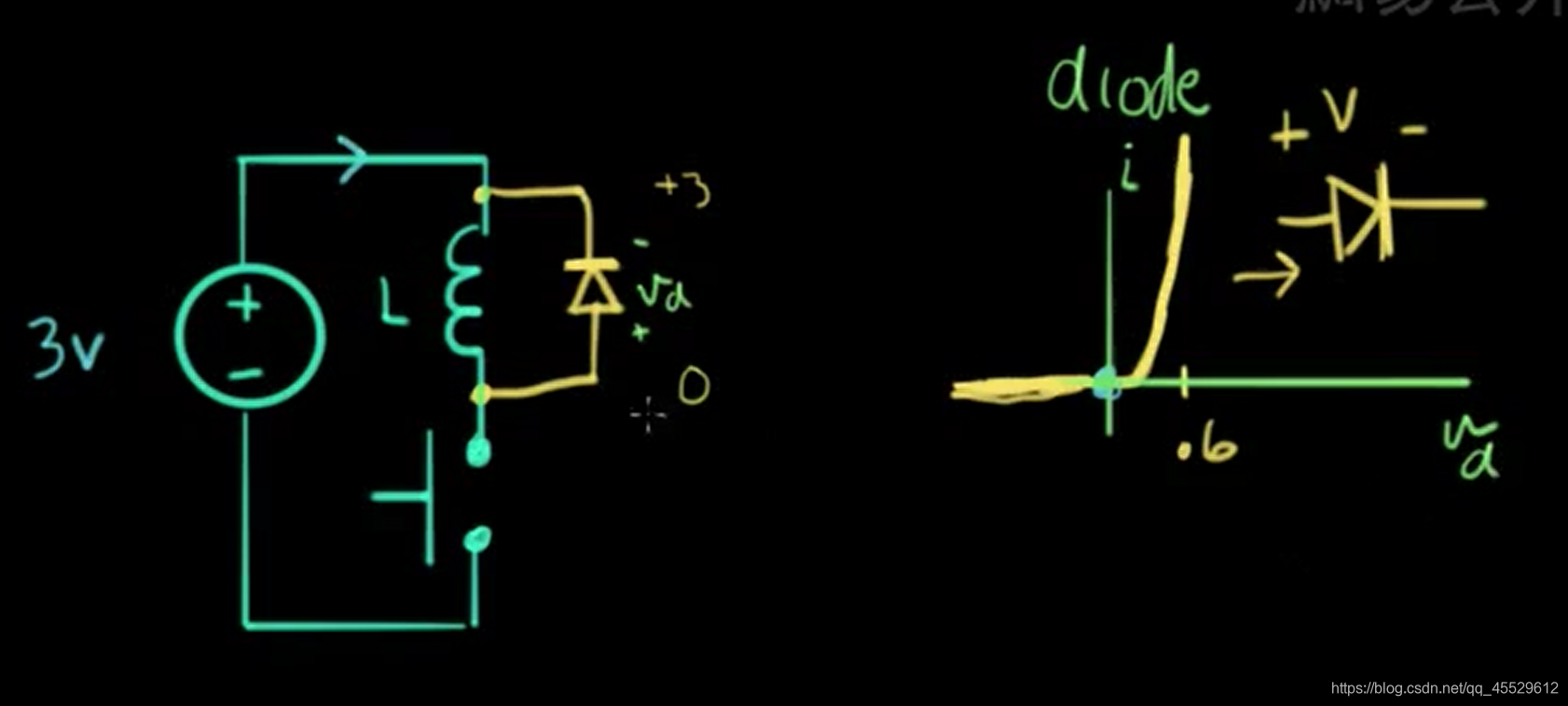
RC 电路求解

自然响应

---

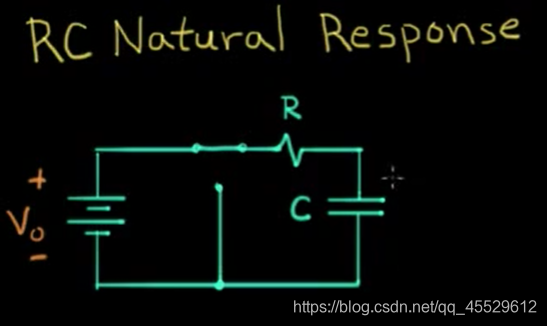
$u_c$ 和 $i_c$ 关联。
$$u_c(t)=u_0{e}^{-\frac{t}{RC}}$$$$i_c(t)=-\frac{u_0}{R}{e}^{-\frac{t}{RC}}$$

阶跃响应

---

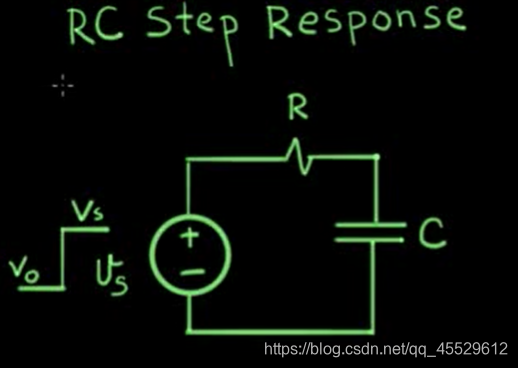
$$u_c(t)=(u_0-u_s)e^{-\frac{t}{RC}}+u_s$$$$i_c(t)=-\frac{u_s-u_0}{R}{e}^{-\frac{t}{RC}}$$

求解阶跃响应时常微分方程解法的物理意义

求解一阶线性常微分非齐次方程的时候，用到了叠加法，把 全响应 分成了 自然响应 和 强迫响应。

求解 自然响应 就是解对应的齐次方程，而求解 强迫响应 则是求解非齐次方程的一个特解。

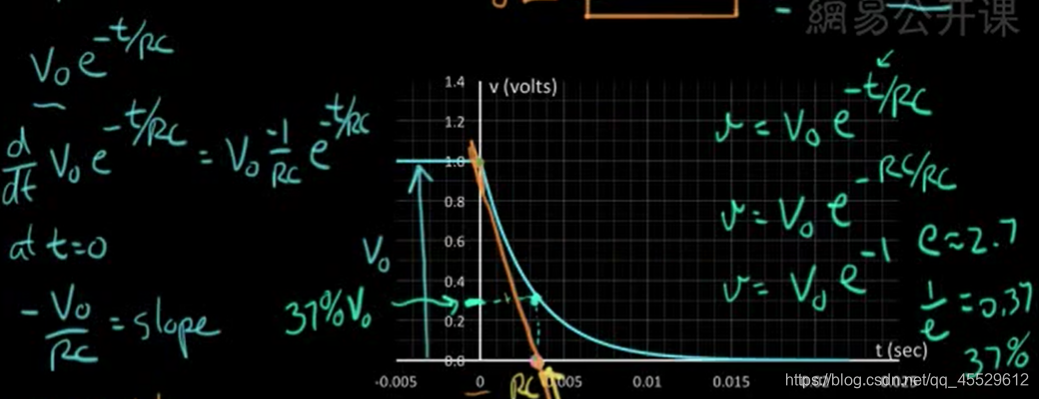
绘制电容电压随阶跃电压变化的指数型曲线草图

初始点切线斜率 $-\frac{u_0}{RC}$
如果是递减，则时间为RC时，函数值约为初始值的 37%

LC自然响应

根据元件电磁特性方程和基尔霍夫定律列出微分方程

解得
$$\begin{gathered} u=u_{0}cos(\sqrt{\frac{1}{LC}}t) \\ i=u_0\sqrt{\frac{C}{L}}sin(\sqrt{\frac{1}{LC}}t) \end{gathered}$$

正弦恒稳态分析

（阻抗）

把正余弦激励写成复指数形式，求解三种无源元件端口的电压与电流的比值，也就是阻抗，从而对电路元件进行了转换。

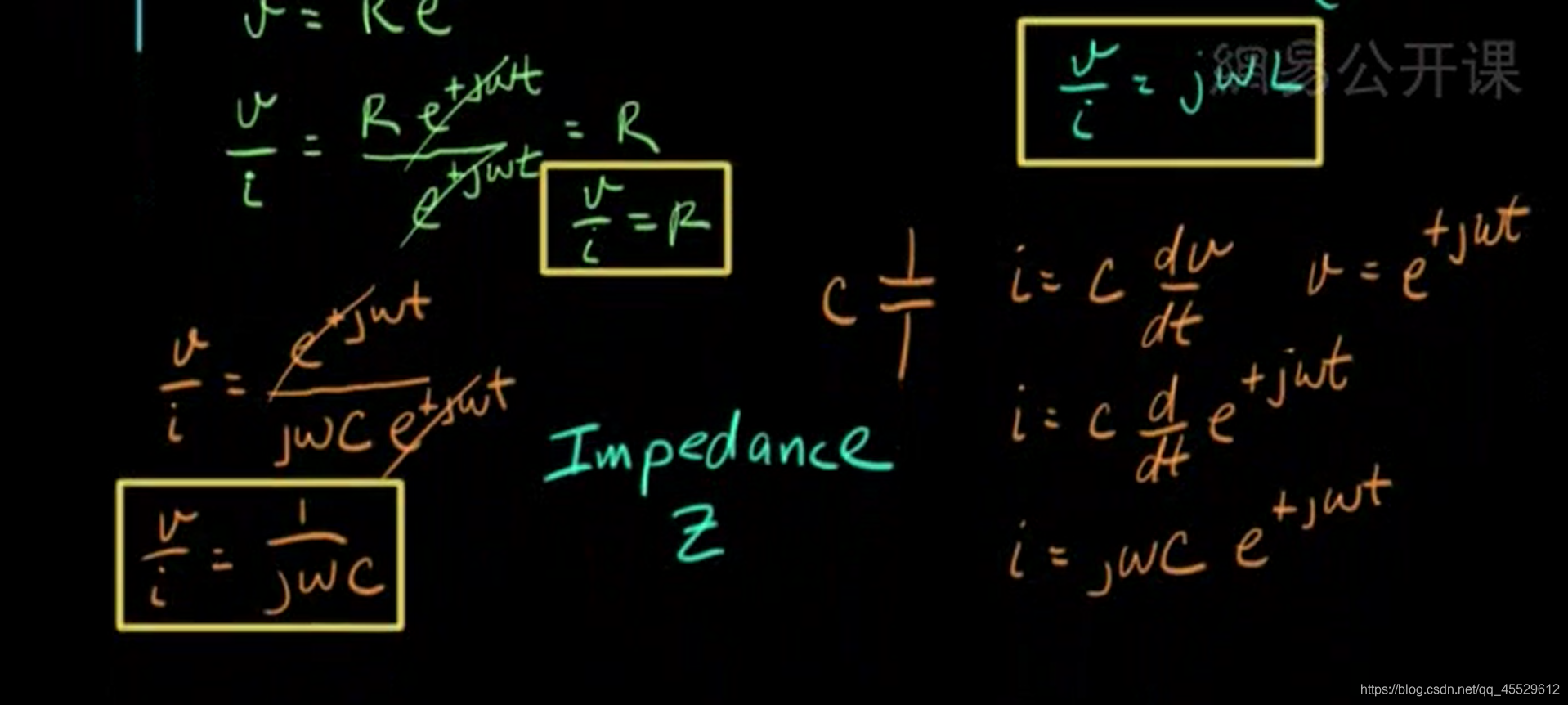
$$\begin{gathered} Z_R=R \\ {Z}_L=j\omega L \\ {Z}_C=\frac{1}{j\omega C} \end{gathered}$$