
背景
树, 是一种常见的数据结构, 有很多的应用场景, 也是面试中的常客。
比如:树的遍历, 分层打印, 平摊的数据转成树, 等等。
这就需要我们对树这种数据结构有个基础的认识,今天我们就再回顾一下这种数据结构。
正文
今天的内容主要包括:
树二叉树二叉搜索树- 实战题目
树
讲树之前, 我们先回顾下链表。
实际上链表和树, 图,都是有一些联系的。
先看一个单链表的示意图:
每个结点都有个value 和一个next 指向后续结点, 一直向后,串成一个链。
这种结构很方便, 但是也有一定的局限。
比如想想访问中间某个结点的时候,或者倒数第几个结点 就只能从头往后一个一个查, 效率不高。
为解决这种问题,应运而生的方法有很多, 比如双向链表, 每个结点不光有后继结点, 还有前继结点。
其实再观察一下, 不难发现, 如果每个结点的next有两个, 会是怎么样?
就变成了我们所说的树。
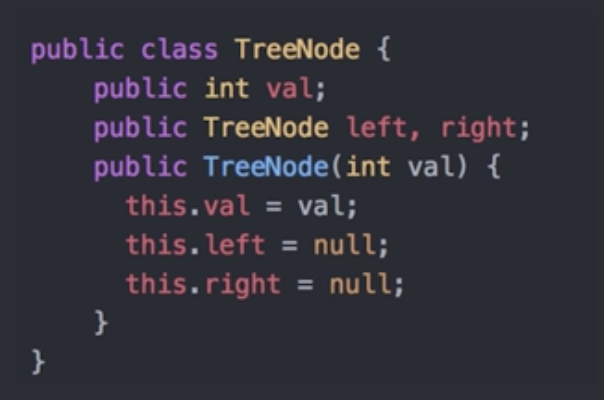
这是一个普通的二叉树的结构, 每个结点有两个next指针, 即左右孩子。
二叉树的一种代码表示:
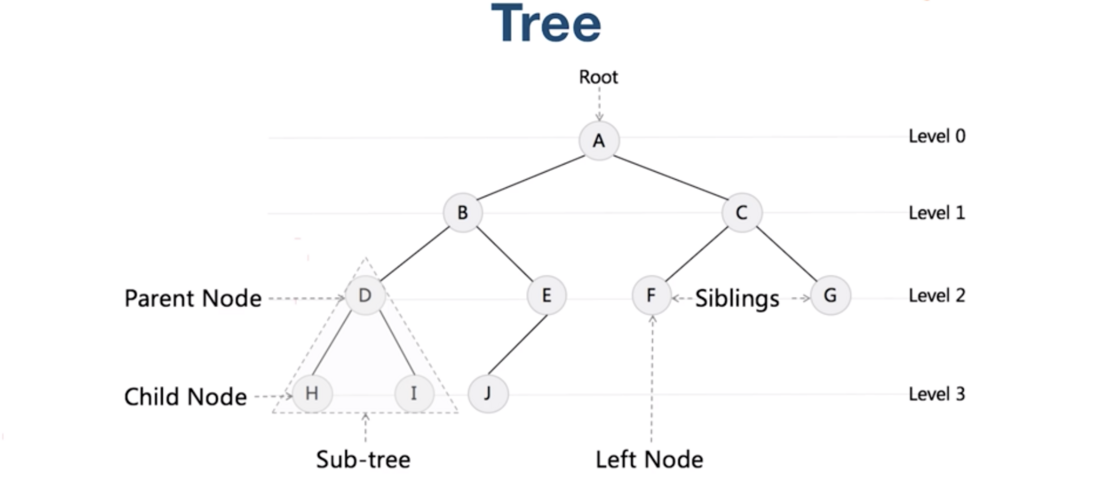
这个特殊的链表的第一个结点, 就是我们说的树的根结点。
树也是分层的, 所谓的层, 就是距离根结点的距离,如上图所示。
二叉树
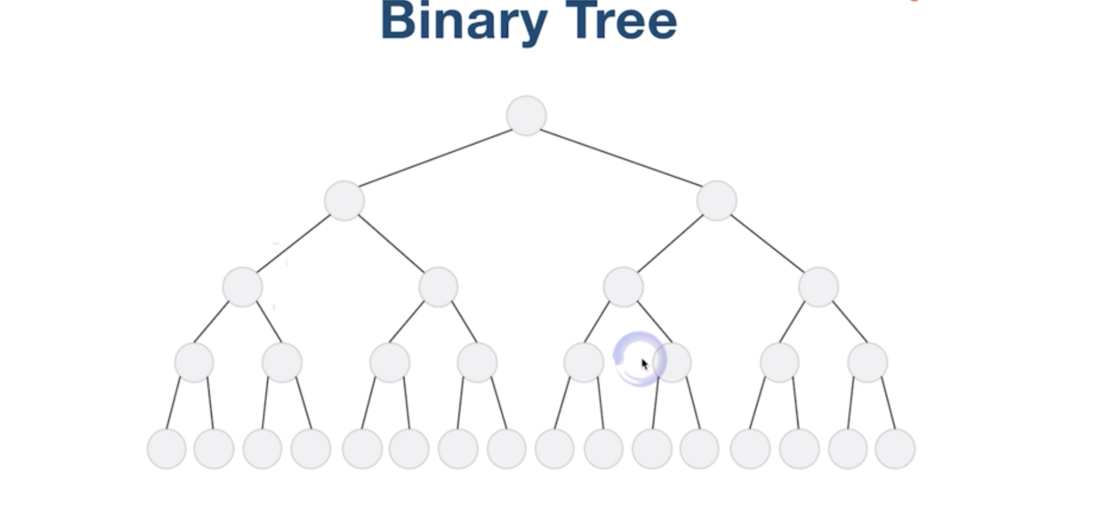
如果每一个结点都有两个孩子结点, 这样的树, 就是满二叉树。
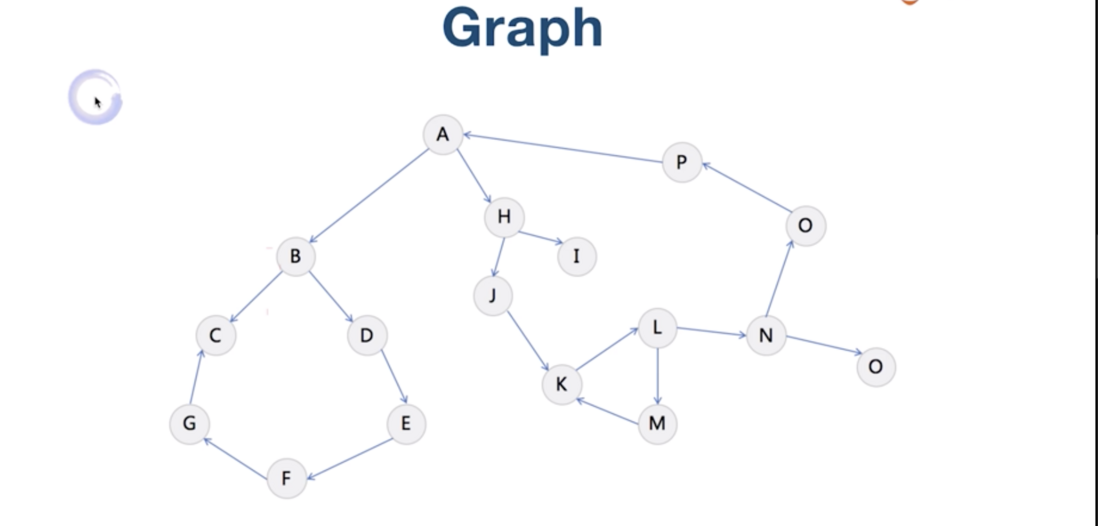
再观察一下, 发现, 如果结点还能指回到根结点,或者其他结点, 这个树会变成什么样?
没错, 就变成了图。
图在我们的生活中也有很多相似的案例, 比如你要走到什么地方, 怎么走最短等等。
简单总结一下:
链表, 就是特殊化的树。
树, 就是特殊化的图。
二叉搜索树
二叉搜索树, 是一种特殊的二叉树。
它可以是一颗空树, 或者是具有下列性质的二叉树:
- 左子树上所有结点的值,均小于它的根结点的值
- 右子树上所有结点的值,均大于它的根结点的值
- 左右子树, 都是一个合法的二叉搜索树。
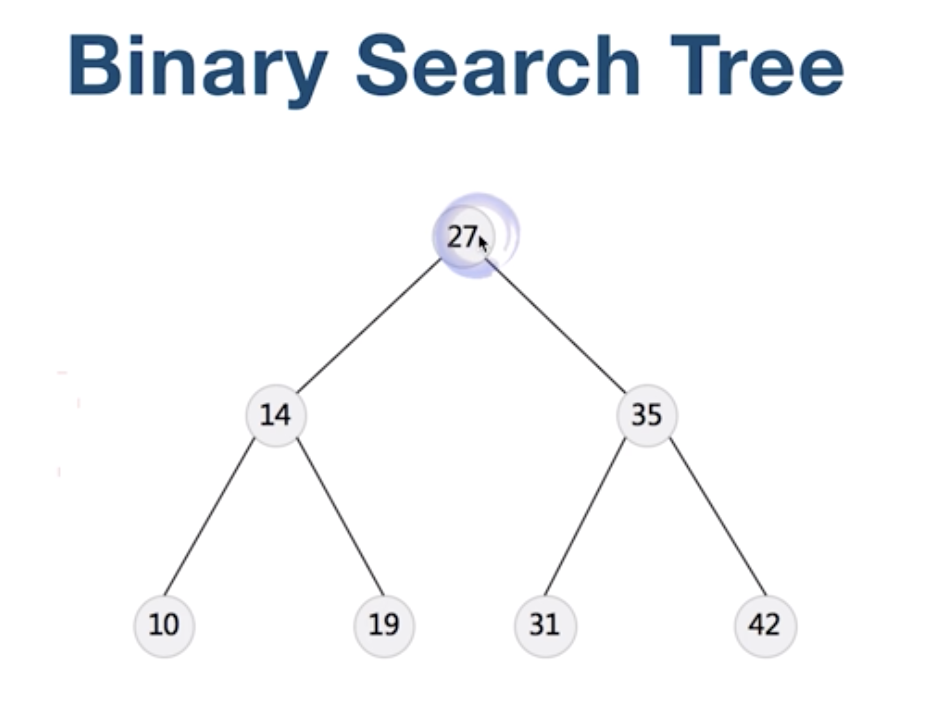
比如:
左孩子上的结点都是小于27的, 后孩子上的结点都是大于27的。
这种结构的好处在于, 比如我们要查找一个元素的时候, 只需要和根比较。
大于根, 就在右子树, 小于就在左子树, 每次搜索, 都能减少一半的数据量。
和链表相比, 查找一个元素, 链表是O(N), 二叉搜索树每次都是减一半, 就变成了O(log2(N)), 效率得以提升。
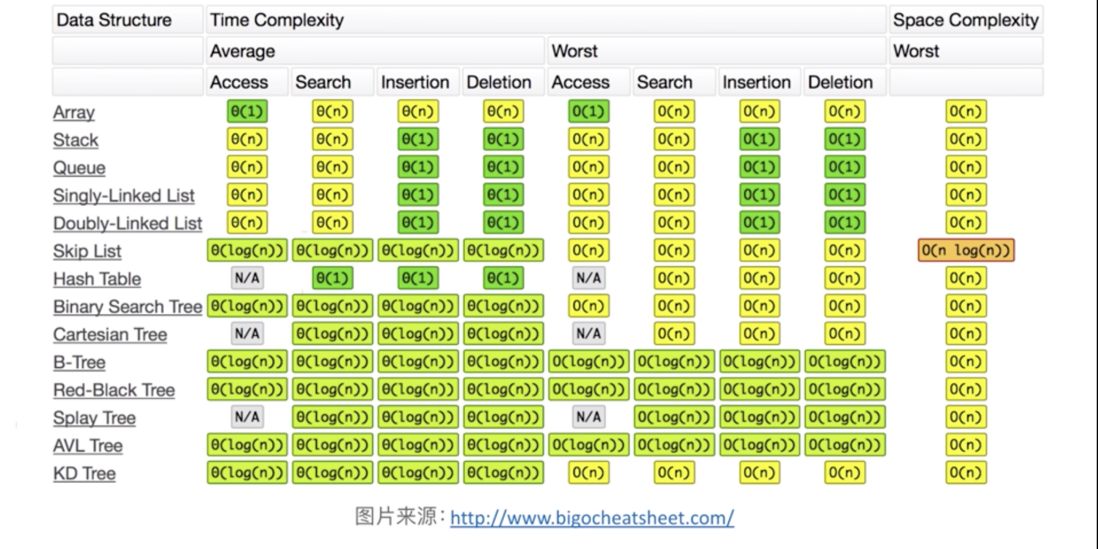
最后献上一个老生常谈的比较图:
二叉搜索树在最坏的情况下,会退化成O(N)的, 比如, 只有右子树, 没有左子树, 就是一条长长的链。
为了改善这种情况, 后面又发展出了各种各样的树, 比如下面的
- 红黑树
- Splay Tree
- AVL Tree
这三种也叫平衡二叉搜索树, 在最坏情况下, 也能保持O(log(n))的时间复杂度
在Java, C++ 的标准库里面,二叉搜索树都是用红黑树来实现的。
对红黑树有兴趣的同学,可以看一下维基百科: https://zh.wikipedia.org/wiki...
理论大概就是这么些, 下面我们就进入到实战环节。
实战题目
验证二叉搜索树
这是leetcode 的第98题, medium 难度。
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
输入:
2
/ \
1 3
输出: true
示例 2:
输入:
5
/ \
1 4
/ \
3 6
输出: false
解释:
输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。
我用了三种解法, 下面我们一个一个看。
解法1: 利用升序特性
观察二叉搜索树, 我们不难发现, 如果是一个合法的二叉搜索数, 一定是左结点 < 根结点 < 右结点
这样得到的中序遍历一定是一个升序的,可以用这种方式来验证。
简单回顾下二叉树的遍历:

比如这个树的中序遍历结果就是: 10 14 19 27 31 35 42
所以利用升序特性, 我们可以得到第一种解法:
var isValidBST = function (root) {
var stack = [];
// 中序遍历
function dfs(root) {
if (!root) return;
root.left && dfs(root.left)
root && stack.push(root.val)
root.right && dfs(root.right)
}
dfs(root)
for (var i = 0; i < stack.length - 1; i++) {
if (stack[i] >= stack[i + 1]) return false
}
return true;
};在观察一下 ,我们不难发现, 左结点 < 根结点 < 右结点, 根结点的值一定是夹在左右结点的值中间的,
如果不在这个范围里, 也一定是不合法的。 所以, 根据这个思路,可以得到解法2.
解法2: 递归
var isValidBST = function (root) {
function isValidBSTHelper(root, min, max) {
if (root == null) return true; // 空树也是合法的
if (root.val <= min || root.val >= max) return false; // 不在范围内, 不合法
return isValidBSTHelper(root.left, min, root.val) && isValidBSTHelper(root.right, root.val, max); // 减少一半数据, 继续往下判断
}
return isValidBSTHelper(root, -Infinity, Infinity)
}这种解法也非常容易理解。
解法3: 利用特性
第三种解法来自网友,也是利用大小的特性.
即: 任意节点的值必须大于其左子树的最右节点;同时小于右子树的最左节点。
从根节点开始检查,一旦发现不满足则返回false.
代码实现:
var isValidBST = function (root) {
function dfs(root) {
if (root == null) return true
if (root.left) {
if (root.left.val >= root.val) return false
let rightest = getRightest(root.left)
if (rightest && rightest.val >= root.val) return false
}
if (root.right) {
if (root.right.val <= root.val) return false
let leftest = getLeftest(root.right)
if (leftest && leftest.val <= root.val) return false
}
return dfs(root.left) && dfs(root.right)
}
function getRightest(node) {
while (node && node.right) node = node.right
return node
}
function getLeftest(node) {
while (node && node.left) node = node.left
return node
}
return dfs(root)
};代码稍显繁琐, 理解一下思路即可。
二叉搜索树的最近公共祖先
这是leetcode 235题。
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x.
满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。这道题我用了两种解法。
解法1: 递归
递归的思路也非常简单:
如果 p, q 都小于root, 说明解在左子树。
如果 p, q 都大于root, 说明解在右子树。
如果一个大于root, 一个小于root, 那root 就是最近的公共祖先。
按照这个思路, 实现代码:
var lowestCommonAncestor = function(root, p, q) {
// p, q 都小于root, 说明解在左子树
if(p.val < root.val && q.val < root.val ) return lowestCommonAncestor(root.left, p, q)
// p, q 都大于root, 说明解在右子树
if(p.val > root.val && q.val > root.val ) return lowestCommonAncestor(root.right, p, q)
return root
}
解法2: 非递归
解法2是解法1的变种, 思路都是一样的, 只不过由递归改成了非递归。
代码实现:
var lowestCommonAncestor = function (root, p, q) {
while (root) {
if (p.val < root.val && q.val < root.val) {
root = root.left
} else if (p.val > root.val && q.val > root.val) {
root = root.right
} else {
return root
}
}
}
结语
这篇文章, 我们回顾了下几种树的概念, 并通过实战巩固了这几个概念。
希望对你有所启发。
最后
觉得内容有帮助可以关注下我的公众号 「 前端e进阶 」,我整理了不同的学习专题。
你也可以联系我,加入我们的学习群。
参考资料
https://time.geekbang.org/cou...



























 407
407

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








