Java之实现使用哈夫曼树进行文件压缩及其原理

1．哈夫曼树

哈夫曼树又称最优树（二叉树），是一类带权路径最短的树。构造这种树的算法最早是由哈夫曼(Huffman)1952年提出，这种树在信息检索中很有用。

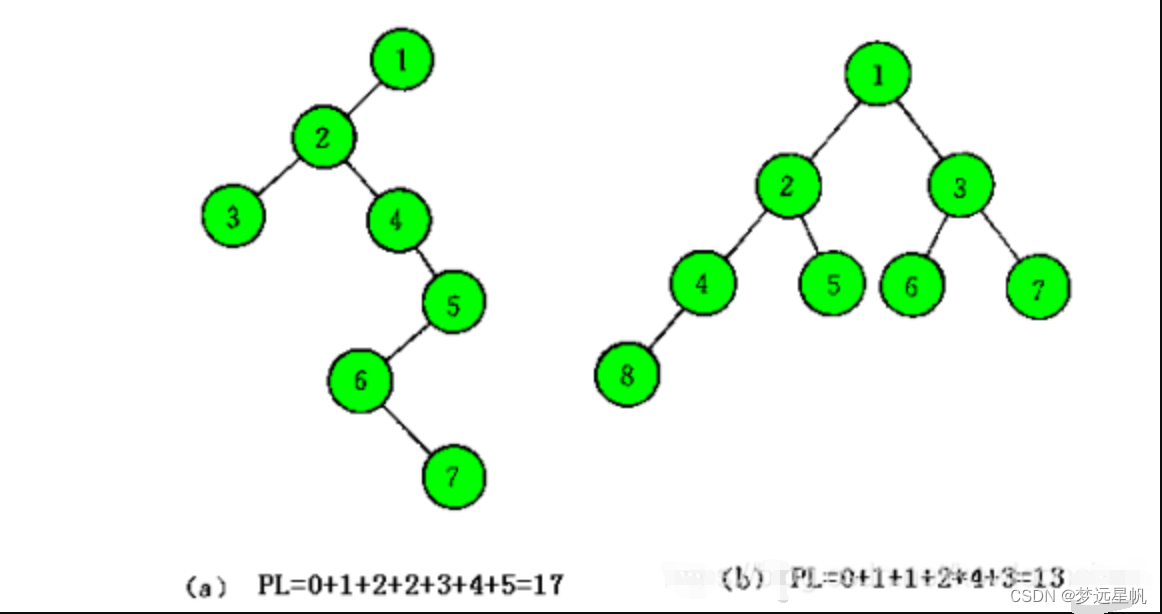
结点之间的路径长度：从一个结点到另一个结点之间的分支数目。

树的路径长度：从树的根到树中每一个结点的路径长度之和。

结点的带权路径长度：从该结点到树根之间的路径长度与结点上权的乘积。

树的带权路径长度：树中所有叶子结点的带权路径长度之和，记作：

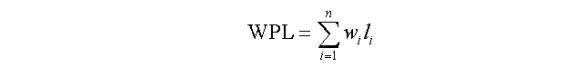
    WPL为最小的二叉树就称作最优二叉树或哈夫曼树。

 

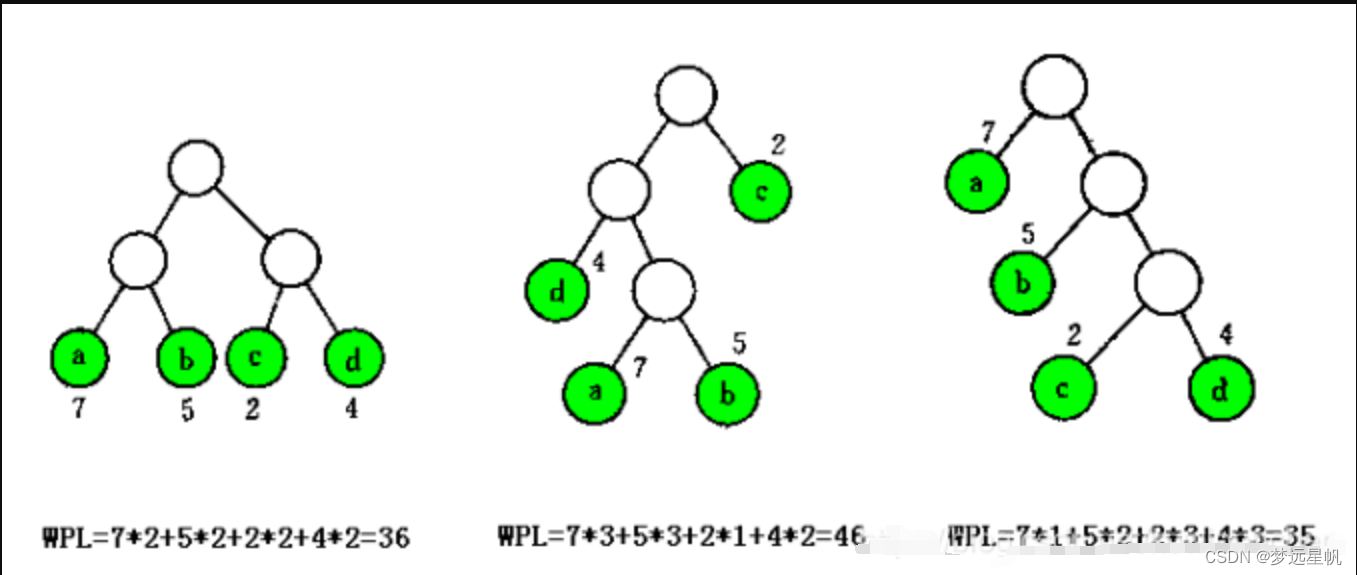
   完全二叉树不一定是最优二叉树。

2. 哈夫曼树的构造
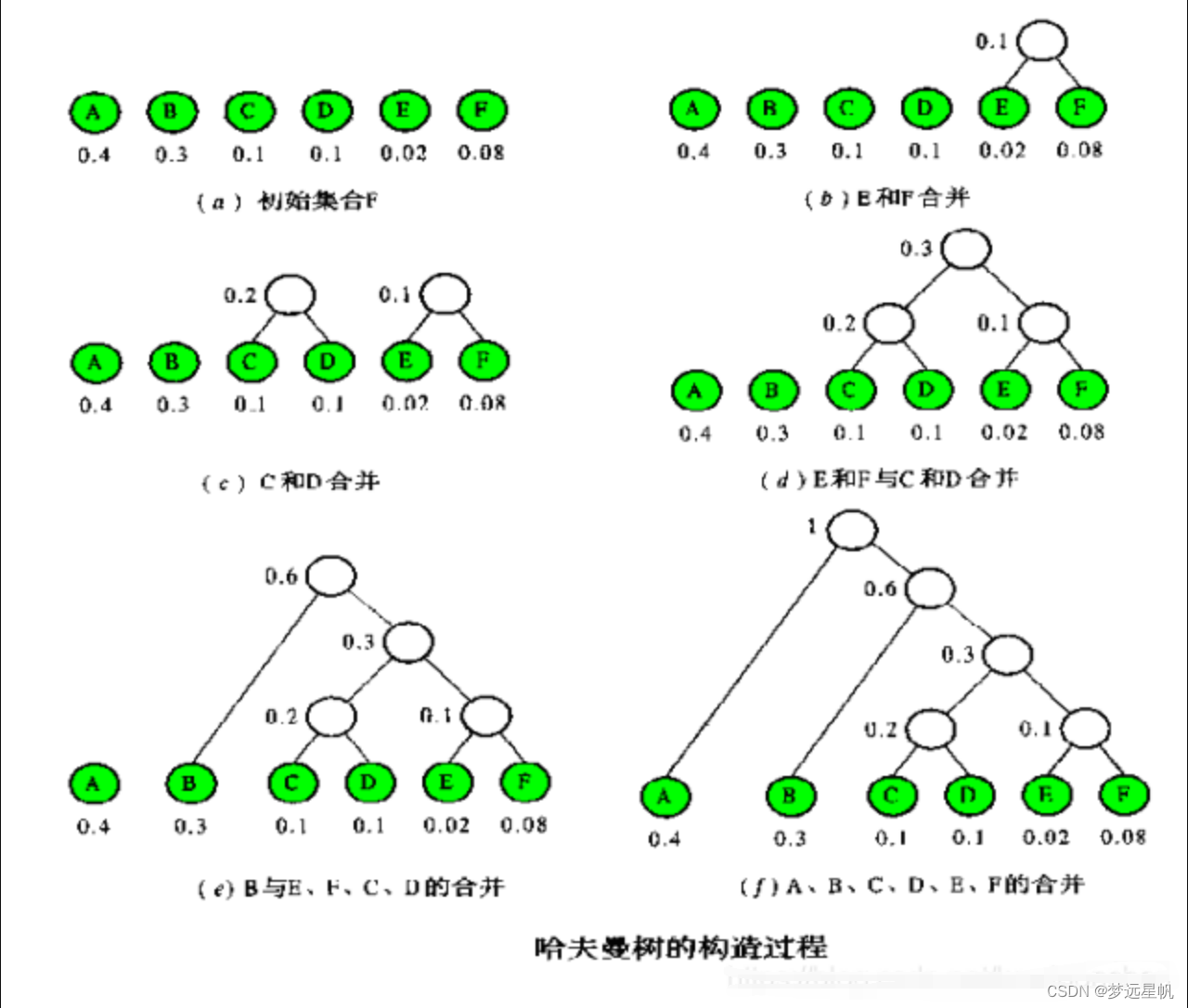
哈夫曼树的构造方式如下：

（1）根据给定的n个权值{w1,w2,...,wn}构造n棵二叉树的集合F={T1,T2,...,Tn}，其中Ti中只有一个权值为wi的根结点，左右子树为空；

（2）在F中选取两棵根结点的权值为最小的数作为左、右子树以构造一棵新的二叉树，且置新的二叉树的根结点的权值为左、右子树上根结点的权值之和。

（3）将新的二叉树加入到F中，删除原两棵根结点权值最小的树；

（4）重复（2）和（3）直到F中只含一棵树为止，这棵树就是哈夫曼树。

例1：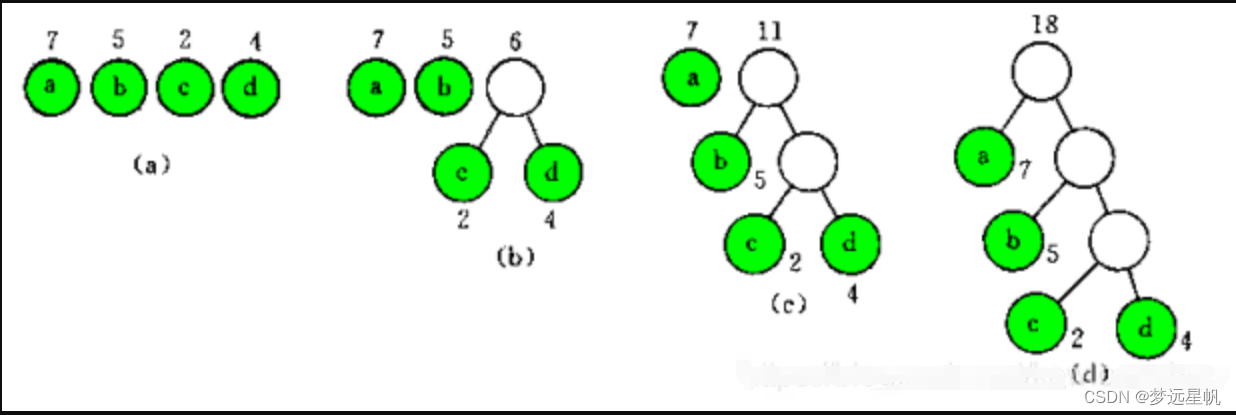

 

例2：

 

3. 哈夫曼树编码
  从哈夫曼树根结点开始，对左子树分配代码“0”，右子树分配代码“1”，一直到达叶子结点为止，然后将从树根沿每条路径到达叶子结点的代码排列起来，便得到了哈夫曼编码。

例，对字符串 EMCAD 编码。若等长编码，则：

   EMCAD => 000001010011100 共15位。

设各字母的出现频率为