第四章贪心策略

最新推荐文章于 2022-05-31 21:03:27 发布

原创

最新推荐文章于 2022-05-31 21:03:27 发布 · 319 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#贪心算法 #算法 #leetcode

本文详细介绍了贪心算法在活动安排问题、最优装载问题、Huffman编码、单源最短路径Dijkstra算法以及最小生成树问题中的应用。通过贪心选择和最优子结构的证明，阐述了贪心策略的有效性，并提供了具体算法的设计思想和实现步骤。

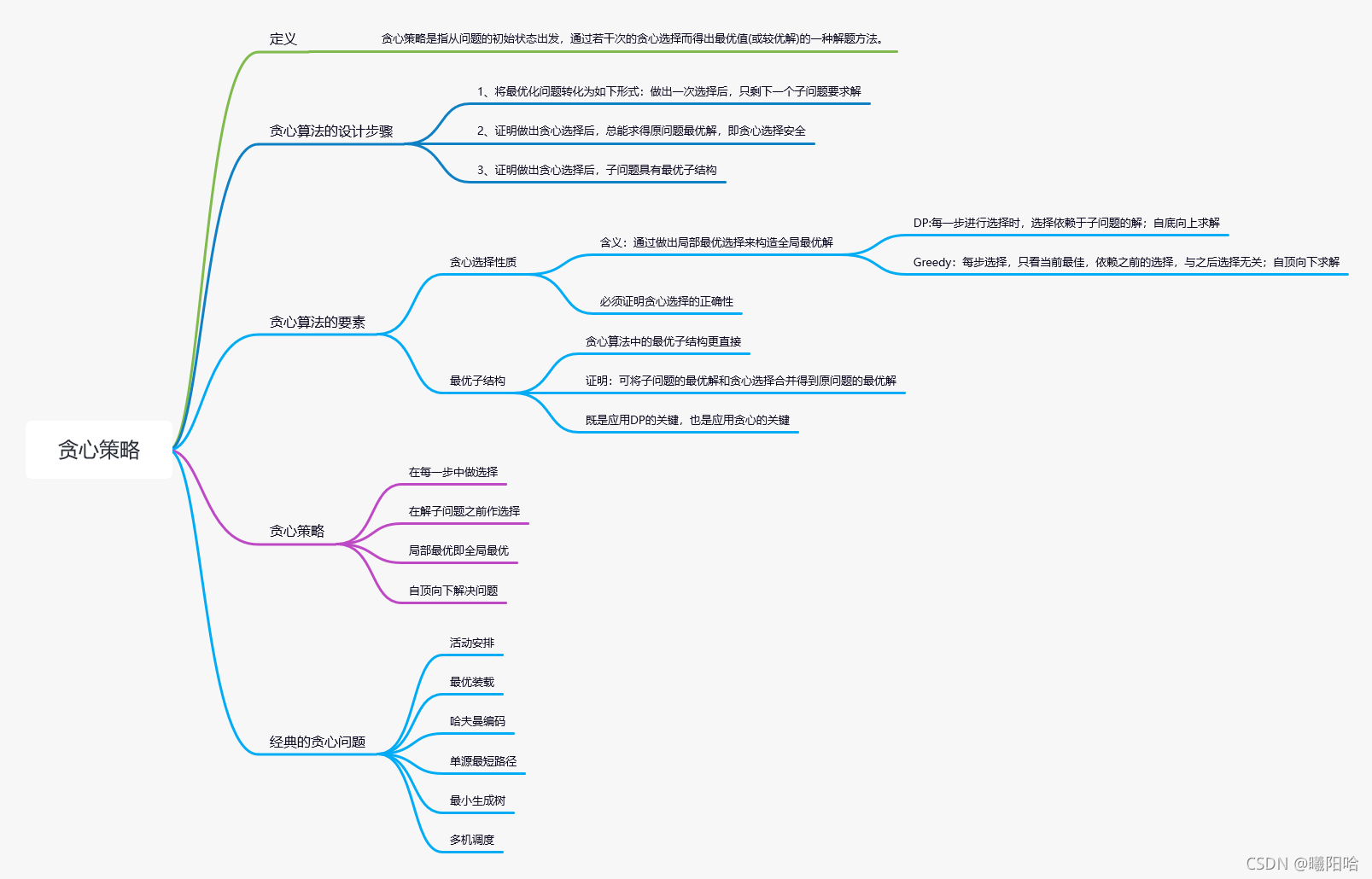
1、活动安排问题

贪心选择：

最数据预处理，即对结束时间排序。贪心选择结束时间最早的活动，若后面的活动开始时间比当前活动的结束时间晚，则安排进来。

最优子结构：

每次选择结束时间早的活动安排进来。

贪心选择的证明：

若活动排序完之后为x1、x2、……xn，其中，x1的结束时间最早，假设该问题的最优值为a，最优解为xi、xi+1……xj，其中ai的结束时间相对于最优解最早，因为xi为最优解的最早结束活动，如果xi就是x1，则贪心选择正确，如果xi!=x1，因为x1是所有活动中结束最早的，所以x1的结束时间必然早于xi的结束时间。所以将最优解当中的xi替换为x1，因为xi为最优解的最早完成活动，而且xi晚于x1结束，所以x1必然早于xi+1……xj所有的活动的开始时间，此时活动个数仍为a，最优值不变，因此贪心选择正确、

最优子结构的证明：

假设原问题的最优值是n，子问题的最优值为m1，子问题之外的活动为集合a