数学分析 第三章 无穷、连续、收敛

无穷小

不能写成 原式=lim(x)*lim(sin(1/x))  因为lim(sin(1/x))没有极限

无穷小阶的比较

等价无穷小的性质

等价代换只能用于乘除，不能用于加减

无穷大及其性质与无穷小类似

连续函数  

对于连续函数，函数符号和极限符号可以交换位置，这对求连续复合函数的极限很有用

定义：

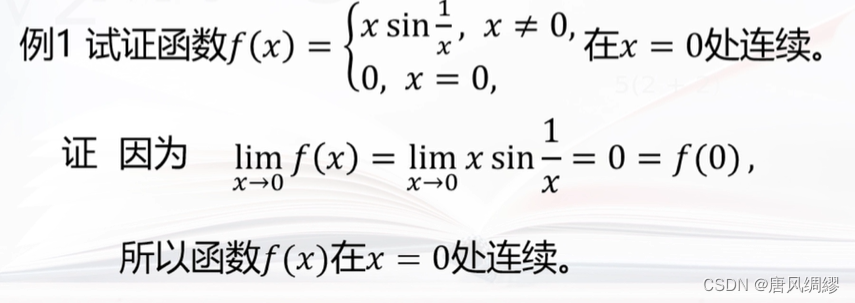
函数单侧连续

函数的间断点

间断点分类

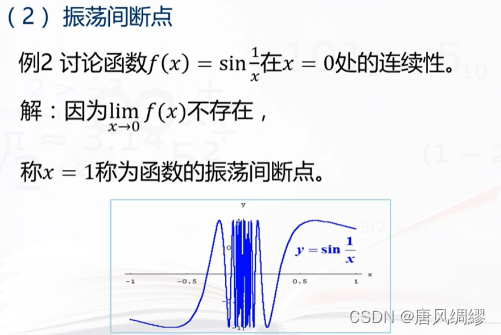
初等函数的连续性

初等函数在它的定义区间内一定是连续的

连续函数有界定理

连续函数最值定理

闭区间  连续  两个条件缺一不可

零点存在定理

连续函数介值定理（零点存在定理的一般化）

函数一致连续的定义

子列收敛定理

确界存在定理:   上确界sup  下确界inf

      下确界同理

例题

  数集有界则必有确界

单调有界原理

柯西收敛准则：柯西收敛<-->数列有极限