线性回归（非线性问题）(python实现)

线性回归（非线性问题）

1.前言

前面通过最小二乘法或梯度下降法解决线性回归的问题，求解出最佳拟合参数，并且通过数据可视化分析。仔细概观察拟合后的图形，我们会发现一些问题。

对于图中标注出的部分，会发现拟合的效果并不理想，是不是通过非线性拟合的方式会更好一些呢？根据这个问题，这里提出两类解决方法，一是局部加权线性回归，二是采用二维二次曲线拟合。

2.局部加权线性回归

在标准线性回归中，所有参与训练的样本点的权重都是一样的，为了体现不同局部的样本点的拟合效果，局部加权线性回归在预测过程中、根据测试数据的不同，赋予每个测试数据不同的权重$C$然后再去求解最佳参数。这里的权重$C$是一个$m$x$m$的对角矩阵
$$c_j^{(i)}=\left[\begin{array}{cccc}{c}_1^{(1)}& 0& ...& 0\\ 0& c_2^{(2)}& ...& 0\\ .& & & \\ .& & & \\ .& & & \\ 0& 0& ...& c_i^{(j)}\end{array}\right](2.1)$$
$c_j^{(i)}$表示第$i$个测试数据在第j个训练样本上的权重$c$，权重计算公式如下
$$c_j^{(i)}=e^{(\frac{{||x_j-x_i||}_2}{-2k^2})}(2.2)$$
$k$值是自定义的参数，$k$越大，说明样本数目越多，$k$越小，说明样本数目越少，在计算过程中，测试样本与训练样本的数据相差越近，则则权重$c$越大。${\left|\left|x_j-x_i\right|\right|}_2$指的是测试样本与训练样本差值取2范数，这里仍然提供两种求解参数的方式，分别是最小二乘法，梯度下降法

1.1最小二乘法

拟合直线方程
$$\hat{Y}=f(x^{(i)})={\theta }_1{x}_1^{(i)}+{\theta }_2{x}_2^{(i)}+...+{\theta }_j{x}_j^{(i)}(2.3)$$
均值方差
$$\frac{1}{m}\sum _{i=1}^m{c}^{(i)}(y^{(i)})-(f(x^{(i)}))(2.4)$$
上标$i$表示第$i$个样本点，将公式2.4转换为矩阵
$$(Y-\hat{Y}{)}^T\ast C\ast (Y-\hat{Y})(2.5)$$
公式2.5对$\theta$求偏导，并令其等于0，即可解得$\theta$的最优参数
$$\theta =(X^{T}CX{)}^{-1}\ast (X^{T}CY)(2.6)$$
根据公式2.6编写代码

#导入科学计算包
from numpy import *
#导入绘图工具
import matplotlib.pyplot as plt
#读取数据文件
def loadDataset(file_name):
    #数据集获取特征数目
    num_feature=len(open(file_name).readline().split('\t'))-1
    #定义并初始化数据集，标签集
    data=[]
    label=[]
    #打开文本文件
    f=open(file_name)
    #对文件按行读取，并迭代每一行
    for line in f.readlines():
        #定义并初始化行列表
        line_list=[]
        #读取文件的每一行数据按按制表符划分
        cur_line=line.strip().split('\t')
        #对划分后的每一个数据迭代加入到行列表中
        for i in range(num_feature):
            line_list.append(float(cur_line[i]))
        #将行列表数据加入到数据集中
        data.append(line_list)
        #将数据标签加入到标签数据集中
        label.append(float(cur_line[-1]))
    return data,label
#根据局部加权线性回归函数求解最佳w拟合
def lwlr(test_data,x_list,y_list,k=1.0):
    x_mat=mat(x_list)
    y_mat=mat(y_list).T
    m=shape(x_mat)[0]
    weights=mat(eye(m))
    for i in range(m):
        diff_mat=test_data-x_mat[i,:]
        weights[i,i]=exp(diff_mat*diff_mat.T/(-2.0*k**2))
    xTx=x_mat.T*(weights*x_mat)
    if linalg.det(xTx)==0.0:
        print("行列式为0，矩阵不可逆")
        return
    w=xTx.I*(x_mat.T*(weights*y_mat))
    print()
    return test_data*w
#打印出散点图
def ploter(x_mat,y_mat,y_prob):
    #绘制散点图
    plt.scatter(x_mat[:,1].tolist(),y_mat.tolist())
    #绘制拟合直线图
    # plt.plot(x_mat[:,1].tolist(),x_mat*w.tolist(),color='red')
    index=x_mat.A[:,1].argsort()
    # print()
    plt.plot(x_mat[:,1].A[index],y_prob[index],color='red')
    plt.show()
#测试
if __name__=='__main__':
    x,y=loadDataset("D:/学习资料/机器学习实战/《机器学习实战》源代码/machinelearninginaction/Ch08/ex0.txt")
    m=shape(x)[0]
    # print(m)
    y_prob=zeros(m)
    for i in range(m):
        y_prob[i]=(lwlr(x[i],x,y,0.01))
    ploter(mat(x),mat(y),y_prob.reshape(200,1))
    # print(shape())

拟合结果图为

1.2梯度下降法

损失函数
$$J({\theta }_1,{\theta }_2,...,{\theta }_j)=\frac{1}{2\ast m}\sum _{i=1}^m{c}^{(i)}(f(x^{(i)})-y^{(i)}{)}^2(2.7)$$
对其求偏导，求梯度
$$\frac{\alpha J}{\alpha \theta }=\frac{1}{m}\sum _{i=1}^m{c}^{(i)}(f(x^{(i)})-y^{(i)})x^{(i)}(2.8)$$
梯度下降更新参数$\theta$,其中$\beta$是学习率
$${\theta }^{new}={\theta }^{old}-\beta \frac{\alpha J^{old}}{\alpha \theta }(2.9)$$
根据梯度下降求解参数的思想，编写代码

#导入科学计算包
from numpy import *
#导入matplotlib绘图库
import matplotlib.pyplot as plt
#获取文本文件处理数据
#读取数据文件
def loadDataset(file_name):
    #数据集获取特征数目
    num_feature=len(open(file_name).readline().split('\t'))-1
    #定义并初始化数据集，标签集
    data=[]
    label=[]
    #打开文本文件
    f=open(file_name)
    #对文件按行读取，并迭代每一行
    for line in f.readlines():
        #定义并初始化行列表
        line_list=[]
        #读取文件的每一行数据按按制表符划分
        cur_line=line.strip().split('\t')
        #对划分后的每一个数据迭代加入到行列表中
        for i in range(num_feature):
            line_list.append(float(cur_line[i]))
        #将行列表数据加入到数据集中
        data.append(line_list)
        #将数据标签加入到标签数据集中
        label.append(float(cur_line[-1]))
    return data,label
# 代价函数对应的梯度函数，
def gradient_function(weights,theta, data, label,m):
    diff = dot(data, theta)- label
    # print(shape(label))
    return (1/m)*(weights*diff).T*data

#计算损招函数
def cal_loss(data,label,theta,m):

    diff=dot(data,theta)-label
    return (1/2*m)*dot(diff.T,diff)
# 梯度下降迭代
def gradient_descent(test_data,data,label,alpha,epochs,k):
    m,n=shape(data)
    theta = ones((n,1))#自定义theta值，
    # 定义权重对角矩阵c
    weights = mat(eye(m))
    # 对对角权重矩阵每一行数据迭代
    for i in range(m):
        # 计算真实值与误差值的差距
        diff_mat = test_data - x_mat[i, :]
        # 根据测试数据与真实数据的差值跟更新权重c
        weights[i, i] = exp(diff_mat * diff_mat.T / (-2.0 * k ** 2))
    gradient = gradient_function(weights,theta,data,label,m)#梯度下降值
    #定义存储损失值列表
    loss_list=list()
    lose=cal_loss(data,label,theta,m)
    #/20000使损失图形显得更直观
    loss_list.append(lose.tolist()[0][0]/20000)
    for i in range(epochs):#迭代次数
        theta = theta - alpha * gradient.T
        # print(shape(lose))
        lose = cal_loss(data,label,theta, m)
        loss_list.append(lose.tolist()[0][0]/20000)
        gradient = gradient_function(weights,theta,data,label,m)
    return test_data*theta,loss_list

#绘制散点图
def ploter(data,label,theta,loss,epochs):
    # 设置中文
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 绘制散点图
    plt.scatter(data[:, 1].tolist(), label.tolist())
    # 绘制拟合直线图
    index = data.A[:, 1].argsort()
    print()
    plt.plot(data[:, 1].A[index], theta[index], color='red')
    plt.show()
    # 绘制损失函数图
    plt.plot(range(epochs+1),loss)
    plt.xlabel("迭代次数")
    plt.ylabel("损失函数值")
    plt.show()


#测试
if __name__=='__main__':
    data,label=loadDataset("D:/学习资料/机器学习实战/《机器学习实战》源代码/machinelearninginaction/Ch08/ex0.txt")
    epochs=200
    m=shape(data)[1]
    #特征维度标准化
    x_mat = mat(data)
    y_mat = mat(label).T
    y_mean = mean(y_mat, 0)
    x_mean = mean(x_mat, 0)
    x_var = var(x_mat, 0)
    x_mat = (x_mat - x_mean) / (max(x_mat)-min(x_mat))
    y_mat = y_mat - y_mean
    x_mat[:, 0] = 1
    loss_list=list()
    m,n = shape(x_mat)
    print(n)
    y_prob = zeros(m)
    # print(x)
    for i in range(m):
        w,loss = (gradient_descent(x_mat[i], x_mat, y_mat, 1,epochs,0.01))
        y_prob[i]=w
        loss_list.append(loss)
    ploter(x_mat, y_mat, y_prob,loss_list[0],epochs)

运行结果图，绘制损失函数图形时,只选择了求解第一个参数的损失函数与迭代关系的图象

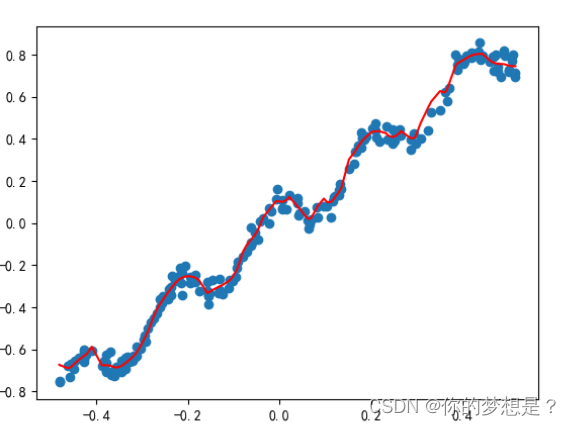
3.高维维高次多项式曲线拟合

基本思想就是，将线性方程改为高维多次多项式，然后求接最优参数，这里只介绍最小二乘法求解，梯度下降法也可以求解
$$\hat{Y}=f(x^{(i)})={\theta }_1{x}_1+{\theta }_2{x}_2^2+...+{\theta }_j{x}_j^n(2.3)$$
代码实现

#导入科学计算包
from numpy import *
#导入matplotlib绘图库
import matplotlib.pyplot as plt
#读取数据文件
def loadDataset(file_name):
    #数据集获取特征数目
    num_feature=len(open(file_name).readline().split('\t'))-1
    #定义并初始化数据集，标签集
    data=[]
    label=[]
    #打开文本文件
    f=open(file_name)
    #对文件按行读取，并迭代每一行
    for line in f.readlines():
        #定义并初始化行列表
        line_list=[]
        #读取文件的每一行数据按按制表符划分
        cur_line=line.strip().split('\t')
        #对划分后的每一个数据迭代加入到行列表中
        for i in range(num_feature):
            line_list.append(float(cur_line[i]))
        #将行列表数据加入到数据集中
        data.append(line_list)
        #将数据标签加入到标签数据集中
        label.append(float(cur_line[-1]))
    return data,label
#处理二次项维度
def two_power(data):
    m=len(data)
    ret_list = list()
    for i in range(m):
        power_two = data[i][1] * data[i][1]
        ret_list.append(power_two)
    return ret_list
#处理三次项维度
def three_power(data):
    m=len(data)
    ret_list=list()
    for i in range(m):
        power_two=data[i][1]*data[i][1]*data[i][1]
        ret_list.append(power_two)
    return ret_list
#处理三次项维度
def flour_power(data):
    m=len(data)
    ret_list=list()
    for i in range(m):
        power_two=data[i][1]*data[i][1]*data[i][1]*data[i][1]
        ret_list.append(power_two)
    return ret_list
#处理三次项维度
def five_power(data):
    m=len(data)
    ret_list=list()
    for i in range(m):
        power_two=data[i][1]*data[i][1]*data[i][1]*data[i][1]*data[i][1]
        ret_list.append(power_two)
    return ret_list
#处理三次项维度
def six_power(data):
    m=len(data)
    ret_list=list()
    for i in range(m):
        power_two=data[i][1]*data[i][1]*data[i][1]*data[i][1]*data[i][1]*data[i][1]
        ret_list.append(power_two)
    return ret_list
#处理三次项维度
def seven_power(data):
    m=len(data)
    ret_list=list()
    for i in range(m):
        power_two=data[i][1]*data[i][1]*data[i][1]*data[i][1]*data[i][1]*data[i][1]*data[i][1]
        ret_list.append(power_two)
    return ret_list
#求解最佳系数w拟合直线方程
def search_best_w(x_mat,y_list):
    #将矩阵转置
    y_mat=mat(y_list).T
    #计算出x的转置*x
    xTx=x_mat.T*x_mat
    #判断行列式值是否为0，为0则矩阵不可逆
    if linalg.det(xTx)==0.0:
        print("矩阵不可逆")
        return
    #计算系数w的公式
    w=xTx.I*(x_mat.T*y_mat)
    return w
#打印出散点图
def ploter(x_mat,y_mat,w):
    #绘制散点图
    plt.scatter(x_mat[:,1].tolist(),y_mat.tolist())
    #绘制拟合直线图
    index = x_mat.A[:, 1].argsort()
    plt.plot(x_mat[:, 1].A[index], (x_mat * w).A[index], color='red')
    plt.show()
#测试
if __name__=='__main__':
    x,y=loadDataset("D:/学习资料/机器学习实战/《机器学习实战》源代码/machinelearninginaction/Ch08/ex0.txt")
    x1=mat(two_power(x)).reshape(200,1)
    x2=mat(three_power(x)).reshape(200,1)
    x3=mat(flour_power(x)).reshape(200,1)
    x4 = mat(five_power(x)).reshape(200, 1)
    x5 = mat(six_power(x)).reshape(200, 1)
    x6 = mat(seven_power(x)).reshape(200, 1)
    x_mat=mat(x)
    x_new_mat=hstack((x_mat, x1))
    x_new_mat = hstack((x_new_mat, x2))
    x_new_mat = hstack((x_new_mat, x3))
    x_new_mat = hstack((x_new_mat, x4))
    x_new_mat = hstack((x_new_mat, x5))
    x_new_mat = hstack((x_new_mat, x6))
    # print(x_mat)
    # print(x_new_mat)
    # print(x1)
    print(shape(x_new_mat))
    w=search_best_w(x_new_mat,y)
    ploter(x_new_mat,mat(y),w)
    print(w)

4.总结

不论是局部加权线性回归，还是多项式解决非线性回归问题，都有很大的可能出现过拟合情况。