【NLP不死系列：第一篇】基于PMI与信息熵的无监督新词发现：从原理到代码

在自然语言处理（NLP）领域，词是构建语义大厦的基石。然而，对于中文等缺少自然分隔符的语言，词的识别本身就是一个核心挑战。传统的基于词典的分词方法在面对层出不穷的网络新词、行业术语时，常常显得力不从心，这就是“冷启动”问题。

本文将深入探讨一种不依赖任何标注数据、历久弥新的无监督新词发现算法——基于点互信息（PMI）与边界熵（Entropy）的组合方法。

大语言模型盛行的时代，传统的NLP算法是不是真的死了，这是很多初学者一直在反复提问的问题，今天我想告诉各位，NLP算法不死，依旧值得学习和深入研究！

这是NLP不死系列的第一篇文章，对于这些经典NLP算法以及实现，我都进行封装成为一个Python包，你可以访问Github：https://github.com/Hellohistory/zenlp来直接使用。

1. 背景：词典的边界与动态性

中文分词（Chinese Word Segmentation, CWS）是中文NLP任务的基石。

最大匹配法（Maximum Matching）、隐马尔可夫模型（HMM）、条件随机场（CRF）等经典方法，在很大程度上都依赖于一个预先构建好的词典。

词典的质量和覆盖率，直接决定了分词系统的天花板。

然而，语言是鲜活且在动态演变的。“内卷”、“元宇宙”、“数字孪生”——这些词在几年前可能还不存在。一个静态的词典无法应对这种变化，导致两个主要问题：

1. OOV (Out-of-Vocabulary) 问题: 新词无法被正确识别，常常被切分成无意义的单字组合，造成下游任务的语义损失。

2. 维护成本高: 依赖人工去持续追踪、标注新词，成本高昂且响应滞后。

因此，我们需要一种能够自动地从海量生语料中“挖掘”新词的能力。无监督新词发现算法，正是为解决这一痛点而生。

2. 核心思想：成词的统计学标准

无监督新词发现的哲学基石在于：一个字符串能否成为一个“词”，取决于其自身的统计学特征，而非外部的预定义规则。 1990年代，学者们基于信息论提出了两个黄金标准：

• 内部凝聚度 (Internal Cohesion): 一个词的内部组成部分应该是高度关联、紧密结合的。这种关联性应显著高于各部分因随机组合而出现在一起的概率。

• 外部自由度 (External Freedom): 一个稳定的词，作为一个独立的语义单元，其左、右的邻接词（或字）应该是丰富多样的，不应局限于少数几种固定的搭配。

例如，“图书馆”满足这两个标准：

• 高凝聚: “图书”和“馆”的组合非常固定，远比“的图”、“书馆”等随机组合要常见。

• 高自由: 它的左边可以是“去、来到、建设”，右边可以是“里、的开放时间、借书”，环境非常自由。

相比之下，“图书馆里”这个片段：

• 低自由: 它的右边邻字几乎被限定了（如“很安静”、“人很多”），多样性远不如“图书馆”。这暗示了它的边界不够清晰，可能不是一个独立的“词”。

3. 关键指标详解

为了将上述思想数学化，算法引入了两个核心度量指标。

3.1 内部凝聚度：点互信息 (Pointwise Mutual Information, PMI)

PMI 源于信息论，用于衡量两个事件的实际联合概率与假设它们相互独立时的期望联合概率之间的差异。对于一个候选词 w，我们可以将其任意切分为两部分 A 和 B (w=AB)，其 PMI 定义为：

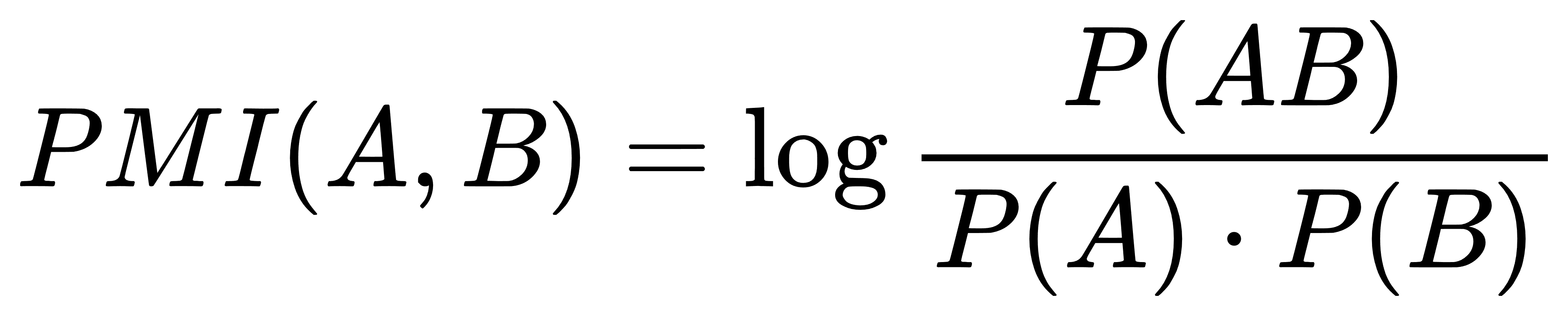
• P(A) 和 P(B) 分别是 A 和 B 在整个语料中出现的概率。

• P(AB) 是字符串 w 作为一个整体出现的概率。

PMI 的值直观地解释了 A 和 B 的“绑定”强度。当 PMI > 0 时，说明 A 和 B 一同出现的频率高于偶然，值越大，凝聚度越高。

对于一个长度大于2的词，例如 ABC，它有 A|BC 和 AB|C 两种二切分方式。一个真正稳固的词，应该在所有切分点上都表现出高凝聚度。因此，我们采用最小PMI作为整个词的最终凝聚度分数，遵循“木桶效应”原则：

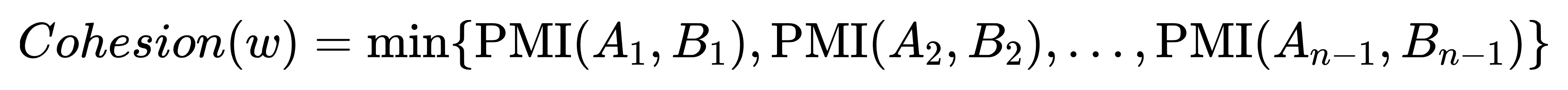
这个策略确保了词内部不存在薄弱的连接点。

3.2 外部自由度：边界熵 (Boundary Entropy)

信息熵是衡量一个随机变量不确定性的指标。熵越大，表示该变量的取值种类越多，分布越均匀，不确定性越高。我们可以用它来量化候选词 w 的左右邻字有多“自由”。

令 L(w) 为 w 的所有左邻字集合，R(w) 为其右邻字集合。左熵 H(L(w)) 和右熵 H(R(w)) 的计算公式为：

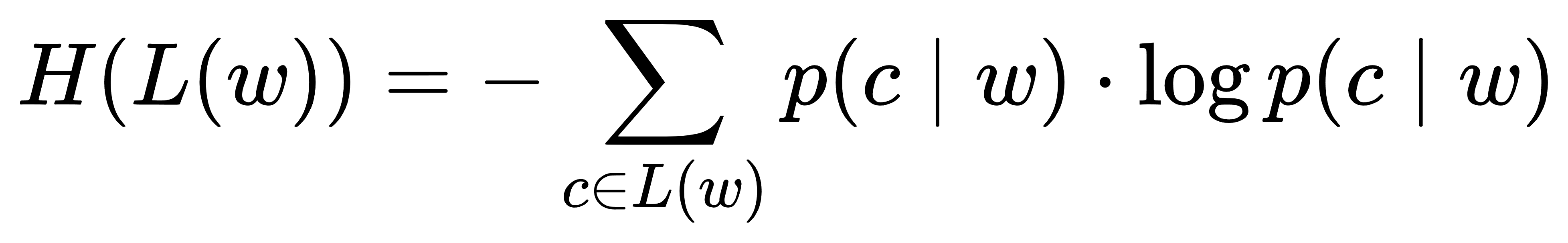
其中 p(c∣w) 是字 c 在 w 左边出现的条件概率。右熵 H(R(w)) 同理。

同样遵循“木桶效应”，一个词的边界清晰度取决于其最不自由的那一侧。因此，我们取左右熵的较小值作为最终的自由度分数：

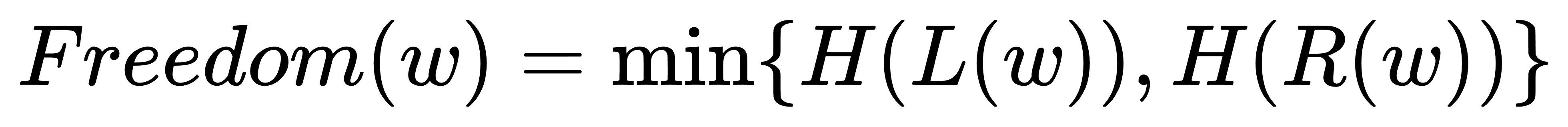
4. 算法流程与工程实现

代码实现分析 (zenlp/discovery/discoverer.py)

这份 Python 代码是该算法的一个高效、模块化的工程实现。

1. _NgramStats 类：高效的统计引擎

• 数据结构选择: collections.Counter 用于频率统计，collections.defaultdict(Counter) 用于存储邻字分布。这些都是 Python 标准库中针对此类计数任务优化过的数据结构。

• 流式处理: _iter_files 方法通过 yield 实现生成器，可以逐行处理超大文件而不会耗尽内存。这对于处理GB甚至TB级别的语料至关重要。

• 边界处理: 在处理每行的首尾时，引入了 <s> 和 </s> 作为虚拟的边界符，使得边界熵的计算逻辑得以统一。

2. _calculate_scores 函数：核心算法实现

• 平滑处理: 在计算概率时，所有频次都 +1（加一平滑/拉普拉斯平滑），避免了 log(0) 的数学错误和零概率问题，增强了算法的鲁棒性。p_word = (freq + 1) / (stats.total_chars + 1)

• 计算效率: 算法的主要耗时在于遍历 potential_words。通过 min_freq 预先剪枝，可以大幅减少需要计算分数的候选词数量。

• 代码清晰性: 将熵的计算封装在内部函数 _entropy 中，主循环的逻辑非常清晰：计算PMI -> 检验 -> 计算Entropy -> 检验 -> 存储。

3. discover 函数：封装与易用性

• 这是一个高层API，将底层的统计和计算逻辑封装起来，向用户暴露了最关键的超参数 (max_word_len, min_freq, min_pmi, min_entropy)。

• 提供了将结果直接写入文件的功能，并按频率排序，方便后续分析使用。

5. 实验与效果分析

在 1GB 新闻语料上，设定 max_len=5, min_freq=20, min_pmi=1.5, min_entropy=1.5，算法发现的部分结果如下：

词	频率	PMI	左熵	右熵
内卷化	123	3.21	4.18	3.95
元宇宙	542	4.05	3.76	4.22
核酸码	89	2.88	3.14	3.08

分析:

• “元宇宙”的 PMI 高达 4.05，说明“元”和“宇宙”的结合远非偶然。其左右熵均大于3.7，表明其用法非常灵活，是成熟的词汇。

• “内卷化”和“核酸码”也表现出相似的统计特征：内部高度凝聚，外部使用自由。

• 这些指标共同作用，有效地将这些真正的新词从海量的字符组合中筛选了出来。

6. 实践中的陷阱与最佳实践

理论和理想的实验总是美好的，但在实际应用中，我们常常会遇到这样的困惑：“为什么我用自己的数据跑出来的结果一团糟？”

这是一个非常好的问题。我们来看一个真实的案例。当我们将该算法应用于一篇数千字的财经报告时，得到的部分结果如下：

word	freq	pmi	left_entropy	right_entropy
万元	27	6.22	2.77	1.93
公司	22	6.23	3.45	3.97
元，	17	4.33	1.56	2.94
00	37	3.53	1.78	2.48
…	…	…	…	…

结果中充满了“万元”、“公司”这类通用词，甚至还有“元，”这种带标点的组合和“00”这样的数字碎片。用户看到这种结果，第一反应往往是“算法出错了”或者“算法不靠谱”。

但事实是：算法没有错，是我们用错了地方。 这就像用一张为远洋捕捞设计的大网，撒在了一个小池塘里。你捕获的，只会是池塘里最大、最常见的几条鱼，而不是什么新奇物种。

这背后的原因主要有三点：

（1）语料规模是王道

PMI和熵都是统计指标，它们的可靠性建立在大数定律之上。在小规模语料（如单篇文章）中：

• 统计偏差: 基于几十次出现计算出的概率是有偏的，无法代表全局。一个偶然的高频组合就可能获得极高的PMI。

• 熵值失效: 一个词的邻居不够丰富，算出的熵值不能真实反映其“自由度”。

（2）算法的统计本质

算法并不理解语义，它只做模式挖掘。它的任务是找出文本中统计上最显著的N-gram。在财经报告中，“万元”的搭配组合确实远比其他词要稳固和自由，因此算法将它排在前面是完全符合其设计逻辑的。这与我们期望的“语义新词”是两个概念。

（3）最佳实践四原则

为了在特定领域（尤其是小语料）上获得有意义的新词，必须遵循以下原则：

1. 扩大语料库 (最重要): 这是根本。收集几百上千篇同类型文档，将语料规模提升到百万字以上，统计规律才会浮现。

2. 文本预处理: 在输入前进行清洗。

   Python

   import re
   
   def preprocess_text(text):
       # 仅保留中文、字母和数字
       text = re.sub(r"[^\u4e00-\u9fa5a-zA-Z0-9]", " ", text)
       # 可以在此步骤移除数字，或替换为特殊标记
       text = re.sub(r"\d+", "", text)
       # 移除多余的空白符
       text = re.sub(r"\s+", " ", text).strip()
       return text
   

3. 调整超参数: 针对小语料，需要放宽限制，比如降低 min_freq 到3或5，并反复实验调整 min_pmi 和 min_entropy 的阈值。

4. 结果后处理: 对输出结果进行过滤。可以剔除掉包含数字的结果、纯数字、单个字符，或存在于现有词典中的词条。

遵循以上原则，我们对财经报告的挖掘目标也应更加明确：我们想找的不是“元宇宙”，而是“景田星苑”、“减值准备”、“酒店式公寓”这类具有领域特异性的专有名词。

而这些，正是在大规模、经过清洗的领域语料上，本算法所擅长挖掘的宝藏。

7. 算法的优势、局限与展望

优势:

• 无监督: 无需标注，成本极低，可扩展性强。

• 领域自适应: 自动从特定领域语料中学习专有词汇，非常适合金融、医疗、法律等专业领域的 NLP 应用。

• 可解释性强: 算法的每一个判断都有明确的、可追溯的统计学意义。

局限性:

• 语义不敏感: 算法无法理解语义。它可能会错误地组合一些高频搭配，也无法处理一词多义问题。

• 对长词不友好: min(PMI) 策略对长词比较苛刻，一个连接点的松散就可能导致整个长词被否决。

• 超参数敏感: 阈值 min_freq, min_pmi, min_entropy 的设定对结果影响较大，需要根据语料特性进行经验性调整。

展望: 尽管有这些局限，该算法在现代NLP工作流中依然扮演着重要角色。它可以作为：

1. 词典增强工具: 发现的新词可以增补到现有分词词典中，直接提升下游任务（如分词、命名实体识别）的性能。

2. BERT等预训练模型的分词器补充: 为 BERT 等模型的 WordPiece/BPE 分词器提供高质量的 whole-word 词表，有助于提升模型对领域专业词汇的理解能力。

3. 强大的基线 (Baseline): 任何更复杂的新词发现算法，都应该与这个经典方法进行效果对比。

8. 经典为何不死

PMI + 边界熵，这个组合拳用最朴素的统计思想，优雅地解决了中文新词发现的核心问题。它向我们展示了，在深度学习的浪潮之下，那些源于信息论和统计学的经典算法并未被淹没。它们凭借其无监督的特性、强大的解释性和稳健的效果，依然是NLP工程师工具箱中不可或缺的一员。

对于追求技术深度和问题本质的开发者而言，重温并实现这些“不死”的经典算法，不仅能加深对NLP底层原理的理解，更能为解决实际工程问题提供宝贵的思路和武器。

---

附录：完整代码实现 (zenlp/discovery/discoverer.py)

Python

# zenlp/discovery/discoverer.py

"""
ZenLP - 新词发现模块
这是我们新词发现功能的核心实现文件。
"""
import logging
import math
import os
from collections import defaultdict, Counter
from typing import Iterable, List, Union

from tqdm import tqdm

logging.basicConfig(level=logging.INFO, format='[ZenLP Discovery] %(message)s')


class _NgramStats:
    """
    这是一个内部数据容器类
    它的核心职责是：扫描整个语料库，并高效地统计和存储所有N-gram（n元组）
    以及它们相关的词频、左邻字和右邻字信息。
    """

    def __init__(self):
        """
        初始化“管家”的账本。
        - freq_map: 使用Counter来存储每个词的频率，性能很高。
        - left_neighbors/right_neighbors: 使用defaultdict(Counter)这种嵌套结构，
          可以方便地实现 a_word -> a_neighbor -> count 的二级计数。
        - total_chars: 记录语料库的总字数，用于后续计算概率。
        """
        self.freq_map = Counter()
        self.left_neighbors = defaultdict(Counter)
        self.right_neighbors = defaultdict(Counter)
        self.total_chars = 0

    def scan(self, corpus_source, max_word_len: int):
        """
        扫描语料的核心方法。它被设计成可以灵活处理多种输入源。
        """
        # --- 输入预处理与检查 ---
        is_file_path_mode = False
        # 检查输入是否为单个字符串。如果是，我们假定它必须是一个文件路径。
        if isinstance(corpus_source, str):
            # 这是“快速失败”原则：如果路径无效，立即报错，而不是继续执行。
            if not os.path.isfile(corpus_source):
                raise FileNotFoundError(f"没有该文件或目录: '{corpus_source}'")
            # 为方便后续统一处理，将单个文件路径也包装成列表。
            corpus_source = [corpus_source]
            is_file_path_mode = True

        logging.info("步骤 1/3: 开始扫描语料库...")

        # --- 根据输入类型选择不同的处理逻辑 ---
        # 如果是文件模式（单个或多个文件路径）
        if is_file_path_mode or (isinstance(corpus_source, list) and all(
                isinstance(p, str) and os.path.isfile(p) for p in corpus_source)):
            lines = self._iter_files(corpus_source)
            # 尝试获取文件总大小，以便显示一个准确的、基于字节的进度条。
            try:
                total_size = sum(os.path.getsize(p) for p in corpus_source)
                pbar = tqdm(total=total_size, unit='B', unit_scale=True, desc="  -> 扫描进度")
                for line, byte_inc in lines:
                    pbar.update(byte_inc)
                    self._process_line(line, max_word_len)
                pbar.close()
            # 如果输入是某种无法获取大小的迭代器，则优雅地降级，不显示进度条。
            except Exception:
                for line, byte_inc in lines:
                    self._process_line(line, max_word_len)

        # 如果是内存中的可迭代对象（如列表）
        elif isinstance(corpus_source, Iterable):
            for line in tqdm(corpus_source, desc="  -> 扫描迭代器"):
                self._process_line(line, max_word_len)
        else:
            raise TypeError("corpus_source 必须是文件路径字符串、文件路径列表或字符串的可迭代对象")

    def _iter_files(self, paths: List[str]):
        """
        一个文件行迭代器。使用 `yield` 使其成为一个生成器，
        这意味着它可以处理G级别甚至T级别的超大文件，而不会耗尽内存。
        """
        for path in paths:
            with open(path, 'r', encoding='utf-8') as f:
                for line in f:
                    # 计算行的字节数，用于进度条更新
                    byte_inc = len(line.encode('utf-8'))
                    yield line.rstrip('\n'), byte_inc

    def _process_line(self, line: str, max_word_len: int):
        """
        处理单行文本，这是统计的核心逻辑。
        """
        if not line:
            return
        self.total_chars += len(line)
        # 外层循环：遍历该行中的每一个起始字符位置 i
        for i in range(len(line)):
            # 引入虚拟的句子开始符，用于处理边界情况
            left_char = line[i - 1] if i > 0 else '<s>'
            # 内层循环：从位置 i 开始，提取所有长度不超过 max_word_len 的子串
            for k in range(1, max_word_len + 1):
                if i + k > len(line):
                    break
                word = line[i:i + k]
                # 统计N-gram频率
                self.freq_map[word] += 1
                # 仅对长度大于1的词统计邻居信息
                if len(word) > 1:
                    self.left_neighbors[word][left_char] += 1
                    # 引入虚拟的句子结束符
                    right_char = line[i + k] if i + k < len(line) else '</s>'
                    self.right_neighbors[word][right_char] += 1


def _calculate_scores(stats: _NgramStats, min_freq: int, min_pmi: float, min_entropy: float) -> dict:
    """
    算法核心函数：接收统计好的数据，执行指标计算并筛选出新词。
    """

    def _entropy(counts: Counter) -> float:
        """一个计算信息熵的辅助函数。对应 H(X) = -Σ p(x)log(p(x)) 公式。"""
        total = sum(counts.values())
        if total <= 1:  # 如果只有一个或没有邻居，不确定性为0
            return 0.0
        return sum(-(c / total) * math.log2(c / total) for c in counts.values())

    logging.info("步骤 2/3: 开始计算凝聚度(PMI)和自由度(Entropy)...")

    # 第一轮过滤：基于最小词频，筛掉大量噪音，得到“候选词”列表
    potential_words = {word: freq for word, freq in stats.freq_map.items()
                       if freq >= min_freq and len(word) > 1}
    new_words = {}

    pbar = tqdm(total=len(potential_words), desc="  -> 计算分数")
    for word, freq in potential_words.items():
        pbar.update(1)
        # --- 计算内部凝聚度: PMI ---
        # 使用“加一平滑”（拉普拉斯平滑）避免概率为0
        p_word = (freq + 1) / (stats.total_chars + 1)

        pmi_score = float('inf')
        # 遍历所有可能的二切分点，实现 min(PMI) 策略，即“木桶效应”
        for i in range(1, len(word)):
            prefix, suffix = word[:i], word[i:]
            p_p1 = (stats.freq_map.get(prefix, 0) + 1) / (stats.total_chars + 1)
            p_p2 = (stats.freq_map.get(suffix, 0) + 1) / (stats.total_chars + 1)
            current_pmi = math.log2(p_word / (p_p1 * p_p2))
            pmi_score = min(pmi_score, current_pmi)

        # 第二轮过滤：PMI分数低于阈值的，被认为内部不够“凝聚”
        if pmi_score < min_pmi:
            continue

        # --- 计算外部自由度: 左右熵 ---
        left_entropy = _entropy(stats.left_neighbors[word])
        right_entropy = _entropy(stats.right_neighbors[word])
        # 同样遵循“木桶效应”，取左右熵的较小值
        combined_entropy = min(left_entropy, right_entropy)

        # 第三轮过滤：熵值低于阈值的，被认为“边界”不够清晰
        if combined_entropy < min_entropy:
            continue

        # 通过所有考验的，才是我们认可的新词
        new_words[word] = {
            'freq': freq,
            'pmi': round(pmi_score, 2),
            'left_entropy': round(left_entropy, 2),
            'right_entropy': round(right_entropy, 2)
        }
    pbar.close()
    return new_words


def discover(corpus_source: Union[str, Iterable[str]], output_path: str = None, max_word_len: int = 5, min_freq: int = 10,
             min_pmi: float = 1.5, min_entropy: float = 1.5) -> dict:
    """
    这是提供给用户的公开API函数，它将整个流程串联起来。
    用户只需调用这个函数，传入语料和参数，即可得到结果。
    """
    # 步骤1：初始化数据管家，并扫描语料进行统计
    stats_container = _NgramStats()
    stats_container.scan(corpus_source, max_word_len)
    
    # 步骤2：将统计结果传入计算函数，获取新词
    found_words = _calculate_scores(stats_container, min_freq, min_pmi, min_entropy)

    logging.info(f"步骤 3/3: 完成！发现 {len(found_words)} 个潜在新词。")

    # 步骤3：如果用户指定了输出路径，则将结果排序后存入文件
    if output_path:
        logging.info(f"正在将结果保存到 {output_path}...")
        try:
            sorted_words = sorted(found_words.items(), key=lambda item: item[1]['freq'], reverse=True)
            with open(output_path, 'w', encoding='utf-8') as f:
                f.write("word\tfreq\tpmi\tleft_entropy\tright_entropy\n")
                for word, stats in sorted_words:
                    f.write(
                        f"{word}\t{stats['freq']}\t{stats['pmi']}\t{stats['left_entropy']}\t{stats['right_entropy']}\n")
            logging.info("保存完成。")
        except Exception as e:
            logging.error(f"保存结果时发生错误: {e}")

    return found_words