线性回归（梯度下降）2021-04-16

最新推荐文章于 2022-01-18 17:05:59 发布

小威程序员

最新推荐文章于 2022-01-18 17:05:59 发布

阅读量366

点赞数 5

分类专栏：推荐系统文章标签：机器学习

本文链接：https://blog.csdn.net/qq_52134394/article/details/115761269

版权

推荐系统专栏收录该内容

11 篇文章 1 订阅

订阅专栏

线性回归（+gradient desent）

线性回归

线性回归

基本思想

线性回归是我们高中学习的线性回归的思想延伸，所以本人感觉不是很难接受。
线性回归是通过若干个相关的离散的点来模拟出的能够预测（由自变量改变引起）因变量的线性图线的一种思想和方法。

1，线性回归

1.1线性回归概念

如果研究的线性代数只包含一个自变量和一个因变量，且二者的关系可以通过一条直线近似的刻画时，这种回归就称为一元线性回归。如果回归分析中涉及到两个及以上的自变量，且自变量与因变量是线性关系，就称为多元线性回归。
线性关系：两个变量之间存在一次方函数关系，通俗一点讲，就是如果如果把这两个变量分别作为点的横坐标与纵坐标，其图象是平面上的一条直线，则这两个变量之间的关系就是线性关系。
一元线性代数的公式： $y = a * x + b$
问题：如何才能更好的去模拟现有的线性关系呢？
接下来引入的就是能解决这个问题的方法：构造损失函数（比较洋气一点的名字叫做loss 函数），首先loss函数是个怎样的概念，本人理解，loss函数就是一个把原先函数的预测值（记为 $\hat{y}$ )当做新的自变量，把L当做因变量的函数，表达式表示为 $L=\frac{1}{n}\sum_{i=1}^{n}\quad(\hat{y_i}-y_i)^{2}$ 公式表达了预测值与真实值之间的平均的平方距离，一般称其为MAE（mean square error）均方误差将上面y的函数表达式代入得到： $L(a,b)=\frac{1}{n}\sum_{i=1}^{n}\quad(ax_i+b-y_i)^{2}$ 然后把a和b看成L的自变量，构造完函数就考虑求未知数的问题。

1.2 回归参数的求解方法

1.21 最小二乘法（least square method

不要感觉很陌生，其实我们高中不知道用了多少次，下面的例子中的公式就是由最小二乘法得到的呀，只不过我们很少有人问为什么罢了吧。
求出这样一些未知参数使得样本点和拟合线的总误差（距离）最小
直观感受一下：（图借鉴与知乎某作者）在这里插入图片描述
由于误差有正有负，会有相互抵消的情况存在，所以我们一般求其差的平方。

2.211 看看怎么来？

手工推导：在这里插入图片描述

1.22 梯度下降法（gradient descent,GD）

梯度下降不懂得话，请点击梯度下降
在这里的应用为： $a-\alpha\frac{\delta L}{\delta a}→a$
$b-\alpha\frac{\delta L}{\delta b}→b$

2,一元线性回归实例

为了帮助大家更快的接受这个知识点，我们不如把高中的线性回归例题拿来作为实例：在这里插入图片描述

我们只要解决第二问就行了，我会先归出手工推导一遍，稍后给出相应的代码实现。

2.1 手工推导

在这里插入图片描述

2.2 代码实现

提示：代码中涉及的批量与随机的方法在上面的梯度下降的链接里有讲解。

print ("零件个数与与加工时间表")
print("序号：1     2    3    4")    
print("个数：2     3    4    5")  
print("时间：2.5   3    4    4.5\n")
import matplotlib.pyplot as plt
import matplotlib
from math import pow       #做平方用
import random      #它的引入是为了下面的批量梯度算法的实现
x = [2,3,4,5]
y = [2.5,3,4,4.5]
#线性回归函数为 y=b+a*x
#参数定义
b = 0.1       #对 b 赋值
a = 0.1       #对 a 赋值
alpha = 0.1   #学习率
m = len(x)
count0 = 0
b_list = []
a_list = []
#使用批量梯度下降法
for num in range(10000):
    count0 += 1
    diss = 0   #误差
    deriv0 = 0 #对 b 导数
    deriv1 = 0 #对 a 导数
    #求导
    for i in range(m):
        deriv0 += (b+a*x[i]-y[i])/m
        deriv1 += ((b+a*x[i]-y[i])/m)*x[i]
    #更新 b 和 a
    for i in range(m):
        b = b - alpha*((b+a*x[i]-y[i])/m) 
        a = a - alpha*((b+a*x[i]-y[i])/m)*x[i]
    #求损失函数 J (θ)
    for i in range(m):
        diss = diss + (1/(2*m))*pow((b+a*x[i]-y[i]),2)
    b_list.append(b)
    a_list.append(a)
    #如果误差已经很小，则退出循环
    if diss <= 0.001:
        break
#使用随机梯度下降法
b1 = 0.1        #对 b1 赋值
a1 = 0.1        #对 a1 赋值
count1 = 0
b1_list = []
a1_list = []
for num in range(10000):
    count1 += 1
    diss = 0     #误差
    deriv2 = 0   #对 b1 偏导
    deriv3 = 0   #对 a1 偏导
    #求导
    for i in range(m):
        deriv2 += (b1+a1*x[i]-y[i])/m
        deriv3 += ((b1+a1*x[i]-y[i])/m)*x[i]
    #更新 b 和 a
    for i in range(m):
        b1 = b1 - alpha*((b1+a1*x[i]-y[i])/m) 
        a1 = a1 - alpha*((b1+a1*x[i]-y[i])/m)*x[i]
    #求损失函数 L(a,b)
    rand_i = random.randrange(0,m)
    diss = diss + (1/(2*m))*pow((b1+a1*x[rand_i]-y[rand_i]),2)
    b1_list.append(b1)
    a1_list.append(a1)
    #如果误差已经很小，则退出循环
    if diss <= 0.001:
        break 
print("批量梯度下降最终得到b={}，a={}".format(b,a))
print("           得到的回归函数是：y={}+{}*x".format(b,a))
print("随机梯度下降最终得到b={}，a={}".format(b1,a1))
print("           得到的回归函数是：y={}+{}*x".format(b1,a1))
#画原始数据图和函数图
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
plt.plot(x,y,'bo',label='数据',color='black')
plt.plot(x,[b+a*x for x in x],label='批量梯度下降',color='red')
plt.plot(x,[b1+a1*x for x in x],label='随机梯度下降',color='blue')
plt.xlabel('x（零件个数）')
plt.ylabel('y（加工时间）')
plt.legend()
plt.show()
plt.scatter(range(count0),b_list,s=1)
plt.scatter(range(count0),a_list,s=1)
plt.xlabel('上方为b，下方为a')
plt.show()
plt.scatter(range(count1),b1_list,s=3)
plt.scatter(range(count1),a1_list,s=3)
plt.xlabel('上方为b，下方为a')
plt.show()

代码运行结果：
在这里插入图片描述

其余的两个图像感兴趣的同学可以给我留言，我会在第一时间回评。
以下观点大多借鉴，欢迎大佬指教。

3，多元线性回归及梯度下降*

3.1 定义数据

以下面一组数据为例子：在这里插入图片描述
以上角标作为行索引，以下角标作为列索引
第二行可以写成： $x^{(2)}=\begin{bmatrix} 916\\1201\\5\\...\\33 \end{bmatrix}$
位于第二行第一列的数字写成：
$x^{(2)}_1=916$
以下角标来区分位置，以便于后期运算。

3.2 定义函数

（1）设置一个回归方程：
$h_\theta(x)=\theta_0+\theta_1 x_1+\theta_2x_2+\theta_3x_3+...+\theta_nx_n$
（2）添加一个列向量：
$x_0=\begin{bmatrix} 1&1&1&1...&1\end{bmatrix}^T$
这里的上角标T表示 $x_0$ 矩阵的倒置，就是由行到列变为由列到行，使得其满足矩阵乘法的要求。
这样方程可以写为：
$h_\theta(x)=\theta_0x_0+\theta_1 x_1+\theta_2x_2+\theta_3x_3+...+\theta_nx_n$
既不会影响到方程的结果，而且使x与 $\theta$ 的数量一致以便于矩阵计算。
为了方便表达，分别记为：
$X=\begin{bmatrix} x_0\\x_1\\x_2\\x_3\\...\\x_n \end{bmatrix},\theta=\begin{bmatrix} \theta_0\\\theta_1\\\theta_2\\\theta_3\\...\\\theta_n \end{bmatrix}$
方程再次变形：
$h_\theta(x)=\begin{bmatrix} \theta_0&\theta_1&\theta_2&\theta_3&...&\theta_n \end{bmatrix}_T\begin{bmatrix} x_0\\x_1\\x_2\\x_3\\...\\x_n \end{bmatrix}$
(3)由回归方程推导出损失方程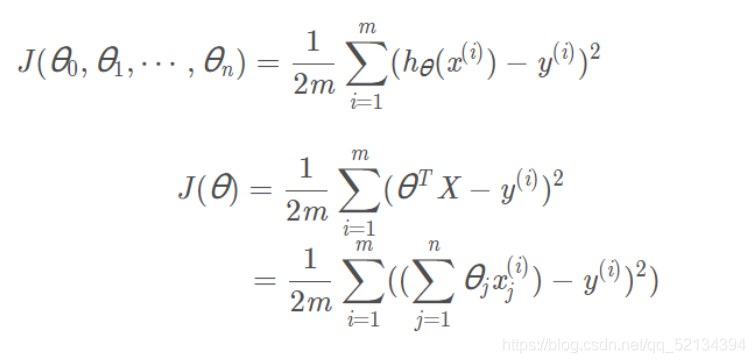：在这里插入图片描述

3.3应用梯度下降

在这里插入图片描述
计算时要一个一个计算，以确保数据统一变化。在执行次数足够多的迭代后，就能取得达到要求的 $\theta_j$ 的值。

3.4 著名的鸢尾花数据集

Iris 鸢尾花数据集内包含 3 类，分别为山鸢尾（Iris-setosa）、变色鸢尾（Iris-versicolor）和维吉尼亚鸢尾（Iris-virginica），共 150 条记录，每类各 50 个数据，每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度，可以通过这 4 个特征预测鸢尾花卉属于哪一品种。这是本文章所使用的鸢尾花数据集： sl：花萼长度；sw：花萼宽度；pl：花瓣长度；pw：花瓣宽度； type：类别：（Iris-setosa、Iris-versicolor、Iris-virginica 三类）
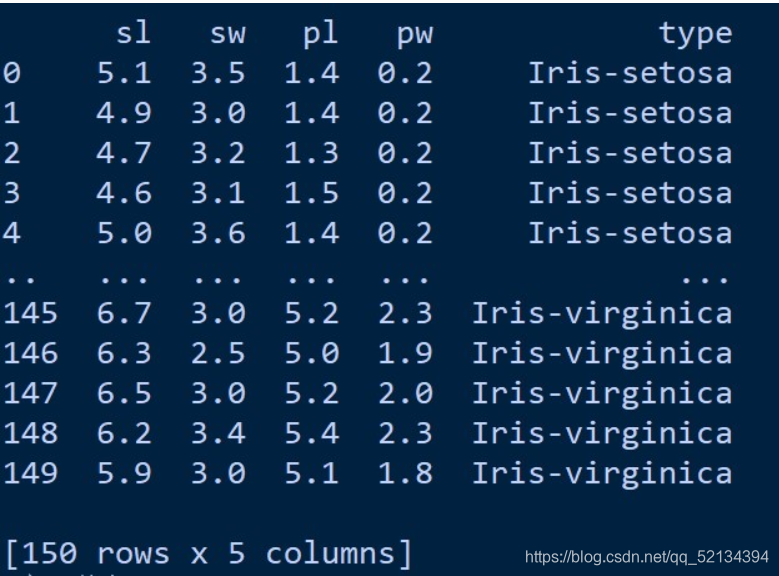
在这里插入图片描述
数据的下载：

鸢尾花数据下载链接
在这里插入图片描述
代码实现：

def MGD_train(X, y, alpha=0.0001, maxIter=1000, theta_old=None):
    '''
    MGD训练线性回归
    传入:
        X       :  已知数据  
        y       :  标签
        alpha   :  学习率
        maxIter :  总迭代次数 
    返回:
        theta : 权重参数
    '''
    # 初始化权重参数
    theta = np.ones(shape=(X.shape[1],))
    if not theta_old is None:
        # 假装是断点续训练
        theta = theta_old.copy()
    
    #axis=1 表示横轴，方向从左到右；axis=0 表示纵轴，方向从上到下
    for i in range(maxIter):
        # 预测
        y_pred = np.sum(X * theta, axis=1)
        # 全部数据得到的梯度
        gradient = np.average((y - y_pred).reshape(-1, 1) * X, axis=0)
        # 更新学习率
        theta += alpha * gradient
    return theta


def SGD_train(X, y, alpha=0.0001, maxIter=1000, theta_old=None):
    '''
    SGD训练线性回归
    传入:
        X       :  已知数据  
        y       :  标签
        alpha   :  学习率
        maxIter :  总迭代次数
        
    返回:
        theta : 权重参数
    '''
    # 初始化权重参数
    theta = np.ones(shape=(X.shape[1],))
    if not theta_old is None:
        # 假装是断点续训练
        theta = theta_old.copy()
    # 数据数量
    data_length = X.shape[0]
    for i in range(maxIter):
        # 随机选择一个数据
        index = np.random.randint(0, data_length)
        # 预测
        y_pred = np.sum(X[index, :] * theta)
        # 一条数据得到的梯度
        gradient = (y[index] - y_pred) * X[index, :]
        # 更新学习率
        theta += alpha * gradient
    return theta
    
    
def MBGD_train(X, y, alpha=0.0001, maxIter=1000, batch_size=10, theta_old=None):
    '''
    MBGD训练线性回归
    传入:
        X          :  已知数据  
        y          :  标签
        alpha      :  学习率
        maxIter    :  总迭代次数
        batch_size :  没一轮喂入的数据数
        
    返回:
        theta : 权重参数
    '''
    # 初始化权重参数
    theta = np.ones(shape=(X.shape[1],))
    
    if not theta_old is None:
        # 假装是断点续训练
        theta = theta_old.copy()
    
    # 所有数据的集合
    all_data = np.concatenate([X, y.reshape(-1, 1)], axis=1)
    for i in range(maxIter):
        # 从全部数据里选 batch_size 个 item
        X_batch_size = np.array(random.choices(all_data, k=batch_size))
        
        # 重新给 X, y 赋值
        X_new = X_batch_size[:, :-1]
        y_new = X_batch_size[:, -1]
        
        # 将数据喂入，更新 theta
        theta = MGD_train(X_new, y_new, alpha=0.0001, maxIter=1, theta_old=theta)
    return theta


def GD_predict(X, theta):
    '''
    用于预测的函数
    传入:
        X     : 数据
        theta : 权重
    返回:
        y_pred: 预测向量
    '''
    y_pred = np.sum(theta * X, axis=1)
    # 实数域空间 -> 离散三值空间，则需要四舍五入
    y_pred = (y_pred + 0.5).astype(int)
    return y_pred 


def calc_accuracy(y, y_pred):
    '''
    计算准确率
    传入:
        y        : 标签
        y_pred   : 预测值
    返回:
        accuracy : 准确率
    '''
    return np.average(y == y_pred)*100

# 读取数据
iris_raw_data = pd.read_csv('iris.data', names  =['sepal length', 'sepal width', 'petal length', 'petal width', 'class'])
# 将三种类型映射成整数
Iris_dir = {'Iris-setosa': 1, 'Iris-versicolor': 2, 'Iris-virginica': 3}
iris_raw_data['class'] = iris_raw_data['class'].apply(lambda x:Iris_dir[x])
# 训练数据 X
iris_data = iris_raw_data.values[:, :-1]
# 标签 y
y = iris_raw_data.values[:, -1]
# 用 MGD 训练的参数
start = time.time()
theta_MGD = MGD_train(iris_data, y)
run_time = time.time() - start
y_pred_MGD = GD_predict(iris_data, theta_MGD)
print("MGD训练1000轮得到的准确率{:.2f}% 运行时间是{:.2f}s".format(calc_accuracy(y, y_pred_MGD), run_time))
# 用 SGD 训练的参数
start = time.time()
theta_SGD = SGD_train(iris_data, y)
run_time = time.time() - start
y_pred_SGD = GD_predict(iris_data, theta_SGD)
print("SGD训练1000轮得到的准确率{:.2f}% 运行时间是{:.2f}s".format(calc_accuracy(y, y_pred_SGD), run_time))
# 用 MBGD 训练的参数
start = time.time()
theta_MBGD = MBGD_train(iris_data, y)
run_time = time.time() - start
y_pred_MBGD = GD_predict(iris_data, theta_MBGD)
print("MBGD训练1000轮得到的准确率{:.2f}% 运行时间是{:.2f}s".format(calc_accuracy(y, y_pred_MBGD), run_time))

小威程序员

关注

5
点赞
踩
7

收藏

觉得还不错? 一键收藏
打赏
0
评论
线性回归（梯度下降）2021-04-16

线性回归（+gradient desent）线性回归基本思想1，线性回归1.1线性回归概念1.2 回归参数的求解方法1.21 最小二乘法（least square method）1.22 梯度下降法（gradient descent,GD）2,一元线性回归实例2.1 手工推导2.2 代码实现线性回归基本思想线性回归是我们高中学习的线性回归的思想延伸，所以本人感觉不是很难接受。线性回归是通过若干个相关的离散的点来模拟出的能够预测（由自变量改变引起）因变量的线性图线的一种思想和方法。1，线性回归1
复制链接

扫一扫