实验二 Python程序流程控制

1. 编写程序计算 1+3+5+7…+99 之和。

sum1 = 0
for i in range(1,100,2):
    sum1 +=i
print(sum1)

2. 编写程序,计算 2+4+6+8…+100 之和。

sum1 = 0
for i in range(2,101,2):
    sum1 +=i
print(sum1)

3. 编写程序,使用不同的实现方法输出 2000~3000 的所有闰年,运行效果如下图所示。

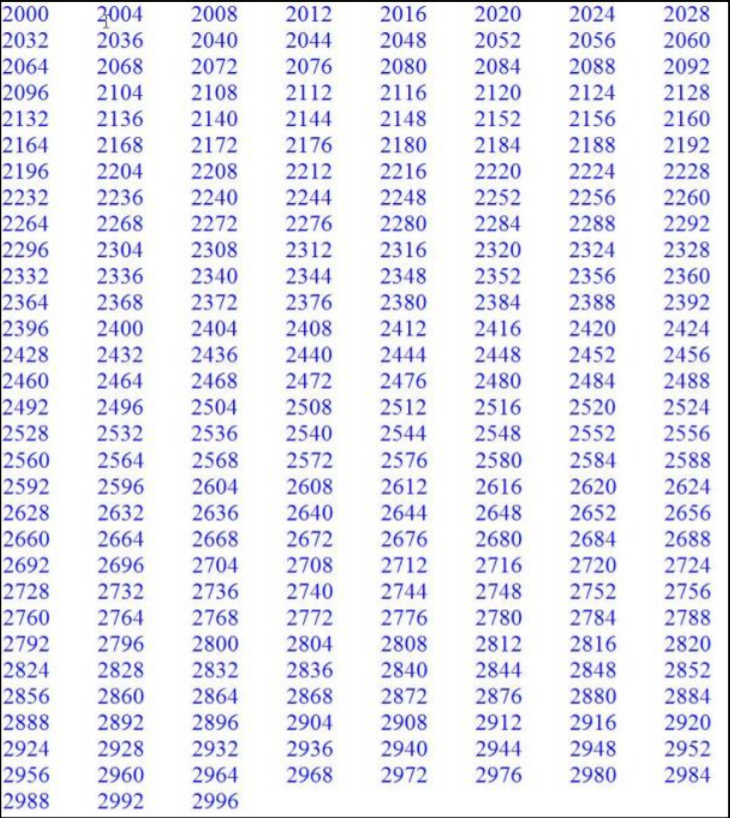
提示：闰年包括普通闰年和世纪闰年，修改 print 函数中的‘end’选项。
1.普通年份能被4整除，且不能被100整除的，是闰年。（如2004年就是闰年）
2.世纪年份能被400整除的是闰年。（如2000年是闰年，1900年不是闰年）

num = 0
for i in range(2000,3001):
    if (i%4==0 and i%100!=0) or i%400==0:
        num+=1
        if num%8==0:
            print(i,end='\n')
        else:
            print(i,end='\t')
    else:
        i=i+1

4. 编写程序,计算 Sn=1-3+5-7+9-11+……n
提示：可以使用%2==0 的语句形式判断 i 是否为偶数。

n=int(input('请输入n的值:'))
##方法一：
Sn = 0
x = -1
for i in range(0,n+1):
    if i % 2==0:  #是偶数
        x=-x
    else:
        Sn+=i*x
print('Sn=',Sn)

###方法二：
sum1=0
sum2=0
for j in range(1,n+1,4):
    sum1+=j
for k in range(3,n+1,4):
    sum2+=k
Sn=sum1-sum2
print('Sn=',Sn)

5. 编写程序,计算 Sn=1+1/2+1/3+…1/n

n = int(input('请输入n的值:'))
x = 1
sum1 = 0
for i in range(1, n + 1, 1):
    x = 1 / i
    sum1 += x
print(f'Sn={sum1:2.2f}')

6.编写程序,打印九九乘法表。（只要实现四种方式中的一种即可）
要求输出九九乘法表的各种显示效果(上三角、下三角、矩形块等方式)

for i in range(1, 10):
    for j in range(1, 11 - i):
        print(f"{10 - i}*{j}={(10 - i) * j}", end='\t')
    print(end='\n')

for i in range(1, 10):
    for j in range(1, i + 1):
        print(f"{i}*{j}={i * j}", end='\t')
    print(end='\n')

7. 编写程序输入三角形的3条边，先判断是否可以构成三角形，如果可以，则进一步求三角形的周长和面积，否则报错“无法构成三角形！”。其运行效果如图下图所示（结果均保留位小数）。

提示: （1）3个数可以构成三角形必须满足如下条件：每条边的边长均大于0，并且任意两边之和大于第三边。
（2）已知三角形的 3 条边，则三角形的面积=根下h*(h-a)*(h-b)*(h-c)，其 中 h 为三角形周长的一半。
（3）其中根号需要导入 math 库并调用 sqrt 函数

import math

a = float(input('请输入三角形的边长a:'))
b = float(input('请输入三角形的边长b:'))
c = float(input('请输入三角形的边长c:'))
print(f'三角形三边分别为:a={a},b={b},c={c}')
l = a + b + c
h = l / 2
area = math.sqrt(h * (h - a) * (h - b) * (h - c))
if a > 0 and b > 0 and c > 0 and a + b > c and a + c > b and b + c > a:
    print(f'三角形的周长={l}')
    print(f'三角形的面积={area}')
else:
    print('无法构成三角形！')

8. 编写程序，输入 x，根据如下公式计算分段函数 y 的值。请分别利用单分支语句双分支结构以及条件运算语句等方法实现。
提示：需要调用 math 模块，其中 math.sqrt()是根号；math.exp()是指数 e； math.log()是 ln；math.sin()是 sin;

import math

x = float(input('请输入X：'))
if x >= 0: y = (x * x - 3 * x) / (x + 1) + 2 * math.pi + math.sin(x)
if x < 0: y = math.log(-5 * x) + 6 * math.sqrt((-x + math.e ** 4)) - (x + 1) ** 3
print(f'方法一：x={x}, y={y}')  # 一句单分支会导致错误
print(f'方法二：x={x}, y={y}')
if x >= 0:
    y = (x * x - 3 * x) / (x + 1) + 2 * math.pi + math.sin(x)
else:
    y = math.log(-5 * x) + 6 * math.sqrt((-x + math.e ** 4)) - (x + 1) ** 3
print(f'方法三：x={x}, y={y}')
y = (x * x - 3 * x) / (x + 1) + 2 * math.pi + math.sin(x) if (x >= 0) else \
    math.log(-5 * x) + 6 * math.sqrt((-x + math.e ** 4)) - (x + 1) ** 3
print(f'方法四：x={x}, y={y}')

9. 编写程序,输入一元二次方程的 3 个系数 a、b 和 c,求 ax²+bx+c=0 方程的解。结果如下图所示

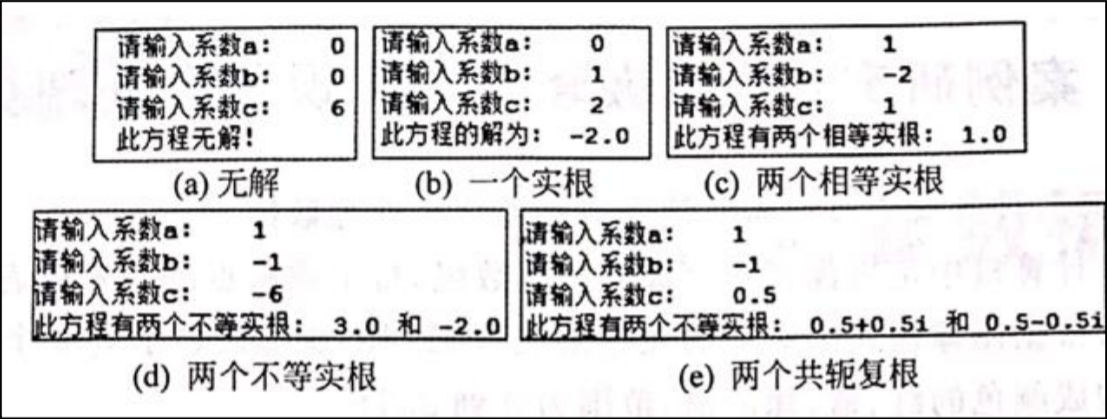
提示：
(1)方程 ax²+bx+c=0 的解有以下几种情况。
①a=0 and b=0,无解。
②a=0andb!=0,有一个实根
③b2-4ac=0,有两个相等实根
④b2-4ac>0,有两个不等实根
⑤b2-4ac<0,有两个共轭复根

(2)可以利用“ print(str.format(“此方程有两个不等实根:{0}+{1}和 {0}-{1}”，realPart，imag Part，)”的语句形式输出方程的两个共轭复根。

import math
a=float(input('请输入系数a：'))
b=float(input('请输入系数b：'))
c=float(input('请输入系数c：'))
d=b*b-4*a*c     #判别式
if a==0 and b==0:  
    print('此方程无解！')
elif a==0 and b!=0:
    print('此方程的解为：',end='')
    x=-c/b
    print(x)
elif d==0:      #判别式等于0 
    print('此方程有两个相等实根：',end='')
    x=(-b)/2*a
    print(x)
elif d>0:       #判别式大于0
    print('此方程有两个不等实根：',end='')
    x1=((-b)+math.sqrt(d))/2*a
    x2=((-b)- math.sqrt(d))/2*a
    print(x1,' 和 ',x2)
elif d<0:      #判别式小于0
    print('此方程有两个共轭复根：',end='')
    real=(-b)/2*a              #实部
    imag=(math.sqrt(-d))/2*a   #虚部
    x1=complex(real,imag)
    x2=complex(real,-imag)
    print(x1,' 和 ',x2)

10. 编写程序，输入整数 n(n≥0)，分别利用 for 循环和 while循环求 n!。

提示： (1) n!=n×(n-1)×(n-2)×…×2×1。例如 5!=5×4×3×2×1=120，特别地，0!=1
(2) 一般情况下，累乘的初值为 1，累加的初值为 0。
(3) 如果输入的是负整数，则继续提示输入非负整数，直到 n≥0。

n = int(input('请输入整数n：'))
s = 1
if n < 0:
    n = int(input('请输入非负整数：'))
elif n == 0:
    print('0!=1')
else:
    for i in range(1, n + 1):
        s *= i
    print(f'  for循环：{n}!={s}')
    s = i = 1
    while i <= n:
        s *= i
        i += 1
    print(f'while循环：{n}!={s}')

11.编写程序,产生两个 0~100(包含 0 和 100)的随机整数 a 和 b,求这两个整数的最大公约数和最小公倍数。

提示：(1)可以利用“ random.randint(0,100)”的语句形式生成 0-100(包含0 和 100)的随机整数。
(2)利用“辗转相除法”求最大公约数,具体算法如下。
①对于已知的两个正整数 m、n,使得 m>n
②m 除以 n 得余数 r
③若 r≠0,则令 m+n，n←r，继续相除得到新的余数 r。若仍然 r≠0，则重复此过程，直到 r=0 为止。最后的 m 就是最大公约数。
(3)求得了最大公约数,最小公倍数就是已知的两个正整数之积除以最大公约数的商。

import random

a = random.randint(0, 100)
b = random.randint(0, 100)
print(f'整数a={a},整数b={b}')
if a < b:
    a, b = b, a

n1 = a
n2 = b
while (n2 != 0):  # 辗转相除法
    t = n1 % n2
    n1 = n2
    n2 = t
print("最大公约数:", n1)
print("最小公倍数:", int(a * b / n1))

直接使用函数方法如下：

import random

a = random.randint(0, 100)
b = random.randint(0, 100)

def gcd(x, y):
    return x if y == 0 else gcd(y, x % y)

print(f'整数a={a},整数b={b}')
print(f'最大公约数={gcd(a, b)},最小公倍数={int(a * b / gcd(a, b))}')