【Luogu】P4127 [AHOI2009] 同类分布 (数位DP)

最新推荐文章于 2025-10-29 20:41:24 发布

原创最新推荐文章于 2025-10-29 20:41:24 发布 · 166 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#深度优先 #算法

P4127 [AHOI2009] 同类分布 - 洛谷

题目：

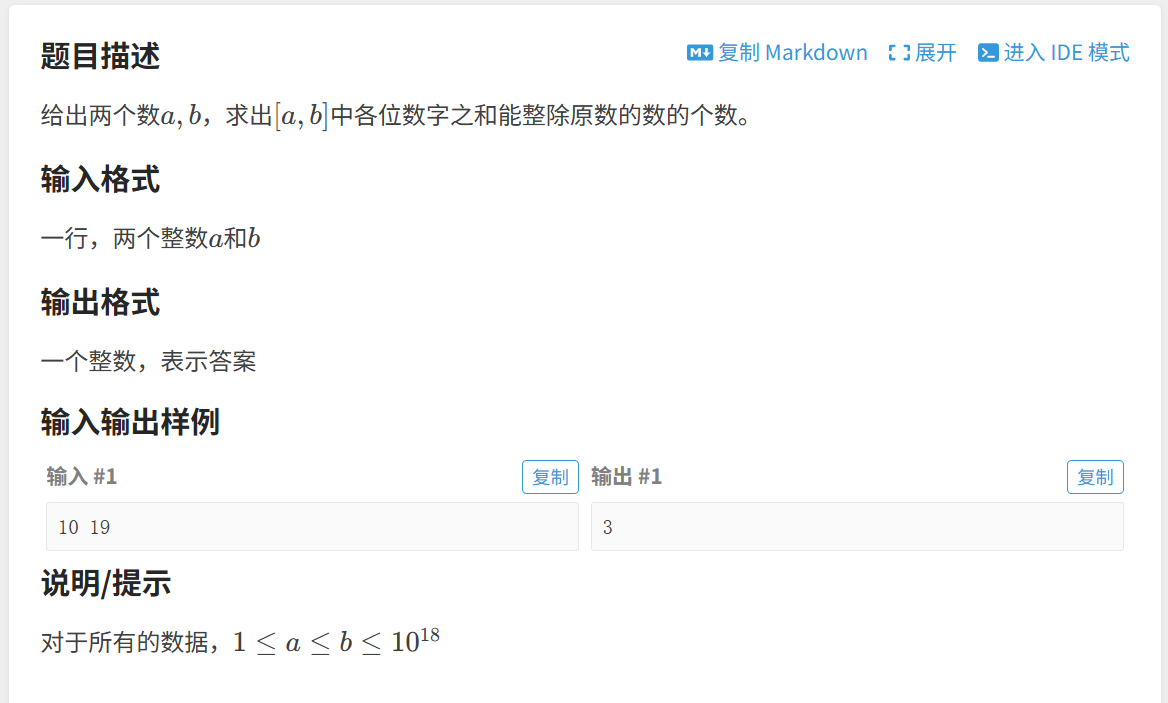
思路：

数位DP板子

一看到统计符合某个特征的数字，那么显然可以想到数位DP

那么板子走起，首先当前位 now 和 lim 肯定有，本题没有前导零的限制，所以可以不需要

那么就分析题目条件来知道还要加什么参数，既然要满足所有数字能被数位和整除，那么显然就需要数位和 sum 这个参数，那么如何处理数字能被数位和整除这个条件呢？如果其当作一个参数，那么记忆化时显然会爆内存，所以考虑优化

发现 18*9=162，数位和的可能很小，所以我们可以考虑提前枚举我们最后的数位和 givesum，那么计算过程中我们只需要传当前的余数 mod 了，这样一来就能快速优化了

PS：下面的代码不应该偷懒使用字符串的，多测时会计算错误，因为我们的最高位是 0，多测记忆化时显然会读取错误，本题不知道为什么能过，应该改成数组比较好的

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
#define Sunny 0
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());

int dp[20][205][205];
int A,B, m, givesum;
string a;

int dfs(int now, int lim, int sum, int mod)
{
    if (now == m)
        return sum == givesum && !mod;
    if (dp[now][sum][mod] != -1 && !lim)
        return dp[now][sum][mod];
    int mx = lim ? a[now] - '0' : 9;
    int res = 0;
    for (int i = 0; i <= mx; i++)
    {
        if (i + sum > givesum)
            break;
        res += dfs(now + 1, lim && i == mx, sum + i, (mod * 10 + i) % givesum);
    }
    if (!lim)
        dp[now][sum][mod] = res;
    return res;
}

int getans(int x)
{
    a = to_string(x);
    m = a.size();
    int ans = 0;
    for (int i = 1; i <= 9 * m; i++)
    {
        memset(dp, -1, sizeof dp);
        givesum = i;
        ans += dfs(0, 1, 0, 0);
    }
    return ans;
}

void solve()
{
    cin >> A >> B;
    cout << getans(B) - getans(A-1) << endl;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int t = 1;
	while(t--)
    {
        solve();
    }
    return Sunny;
}