课堂测试图

最新推荐文章于 2023-11-05 23:34:57 发布

原创最新推荐文章于 2023-11-05 23:34:57 发布 · 689 阅读

6 ·

CC 4.0 BY-SA版权

简阳

文章标签：

#深度优先 #算法 #图论

数据结构专栏收录该内容

8 篇文章

订阅专栏

博客围绕图的相关算法题目展开，包含图的深度优先遍历、广度优先搜索，以及采用prim和kruskal算法求最小生成树权值。详细给出各题的输入输出格式及样例，涉及有向图、无向图等不同情况。

7-1 图深度优先遍历

编写程序对给定的有向图（不一定连通）进行深度优先遍历，图中包含n个顶点，编号为0至n-1。本题限定在深度优先遍历过程中，如果同时出现多个待访问的顶点，则优先选择编号最小的一个进行访问，以顶点0为遍历起点。

输入格式:

输入第一行为两个整数n和e，分别表示图的顶点数和边数，其中n不超过20000，e不超过50。接下来e行表示每条边的信息，每行为两个整数a、b，表示该边的端点编号，但各边并非按端点编号顺序排列。

输出格式:

输出为一行整数，每个整数后一个空格，即该有向图的深度优先遍历结点序列。

输入样例1:

输出样例1:

0 1 2

输入样例2:

输出样例2:

0 1 2 3

#include <bits/stdc++.h>
using namespace std;
#define N 40000
vector<int> h[30100];
bool vis[N];

void dfs(int s){
cout<<s<<" ";
vis[s]=1;
int len=h[s].size();
for(int j=0;j<len;j++){
    if(!vis[h[s][j]])
        dfs(h[s][j]);
}

}
int n,m;
int main(){
	cin>>n>>m;
	int u,v;
	for(int i=0;i<m;i++){
		cin>>u>>v;
		h[u].push_back(v);
		
	}
for(int i = 0 ; i < n ; i ++ )
    sort(h[i].begin(),h[i].end());
	for(int i=0;i<n;i++){
        if(!vis[i])
            dfs(i);
	}



	return 0;
}

7-2 数据结构实验三图的广度优先搜索

以邻接表作存储结构，编写程序对给定的无向图G（包含n个顶点，编号为0至n-1）进行广度优先遍历，并在遍历的过程中计算图G的连通分量个数及边的数目。

本题限定在遍历过程中，如果同时出现多个待访问的顶点，则优先选择编号最小的一个进行访问，以顶点0为遍历起点。

邻接表的类型描述

#define   MaxVexNum  20    //最大顶点数
typedef  struct  ArcNode   //表结点定义
{  
   int  adjvex;
   struct  ArcNode  *nextarc;
}ArcNode;
typedef  struct        //头结点定义
{  
   ArcNode  *firstarc;
}VerNode;
typedef  struct 
{  
   VerNode  vertices[MaxVexNum];
   int   vernum, arcnum;
}ALGraph;

输入格式:

第一行输入图的顶点数和边数e。

接下来共e行。每行代表一条边，输入边依附的两个顶点的编号。用头插法建邻接表，各边按第一个顶点编号升序输入，第一个顶点相同时按第二个顶点降序输入。注意：边不能重复输入。

输出格式:

输出分三行

第一行广度优先遍历序列。序列中每个顶点编号后跟一个空格。
第二行连通分量个数
第三行边数

对于下面给出的无向图G

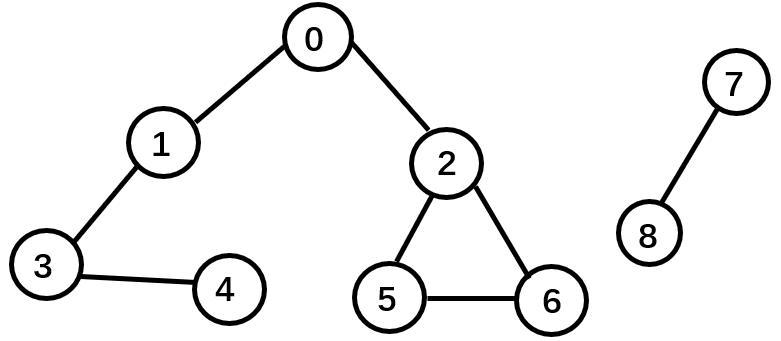
输入样例:

输出样例:

0 1 2 3 5 6 4 7 8 
2
8





#include <bits/stdc++.h>

using namespace std;

#define N 2000000

vector<vector<int>> h(N);

bool st[N];
int n, m;

void bfs(int u)
{
    queue<int> q;
    q.push(u);
    st[u] = 1;
    cout << u << ' ';
    while (q.size())
    {
        int t = q.front();
        q.pop();
        for (auto it : h[t])
        {
            if (!st[it])
            {
                q.push(it);
                st[it] = 1;
                cout << it << ' ';
            }
        }
    }
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; i++)
    {
        int a, b;
        cin >> a >> b;
        h[a].push_back(b);
        h[b].push_back(a);
    }
    for (int i = 0; i < n; i++)
    {
        sort(h[i].begin(), h[i].end());
    }
    int cnt = 0;
    for (int i = 0; i < n; i++)
    {
        if (!st[i])
        {
            cnt++;
            bfs(i);
        }
    }
    cout << endl << cnt << endl;
    cout << m;
    return 0;
}

7-3 计算最小生成树权值

本题要求采用prim算法求最小生成树，输出其权值之和

输入格式:

输入为顶点顶点权值，以 0 0 0表示结束

输出格式:

输出为最小生成树的权值大小

输入样例:

输出样例:

在这里给出相应的输出。例如：

#include <bits/stdc++.h>

using namespace std;

const int N = 1e6 + 10;

struct node
{
    int u, v, w;
};
vector<node> g;
int p[N];
int n, m;

int find(int y)
{
    if (y == p[y])
        return y;
    return p[y] = find(p[y]);
}
set<int> s;
int main()
{
    int a, b, c;
    while (cin >> a >> b >> c)
    {
        if (a == 0 && b == 0 && c == 0)
            break;
        g.push_back({a, b, c});
        s.insert(a);
        s.insert(b);
        p[a] = a;
        p[b] = b;
        m++;
    }
    n = s.size();

    sort(g.begin(), g.end(), [](node a, node b)
         { return a.w < b.w; });

    long long ans = 0, cnt = 0;

    for (int i = 0; i < m; i++)
    {
        int u = g[i].u, v = g[i].v, w = g[i].w;

        u = find(u), v = find(v);
        if (u != v)
        {
            p[u] = v;
            ans += w;
            cnt++;
        }
        if (cnt == n - 1)
            break;
    }
    cout << ans;
    return 0;
}

7-4 最小生成树-kruskal

题目给出一个无向连通图，要求求出其最小生成树的权值。

温馨提示：本题请使用kruskal最小生成树算法。

输入格式:

第一行包含两个整数 N(1<=N<=1x106),M(1<=M<=1x106) 表示该图共有 N 个结点和 M 条无向边。

接下来 M 行每行包含三个整数 Xi,Yi,Zi ，表示有一条长度为 Zi 的无向边连接结点 Xi,Yi 。

输出格式:

输出一个整数表示最小生成树的各边的长度之和。

输入样例:

输出样例:

#include <bits/stdc++.h>

using namespace std;

#define N 2000000

struct node
{
    int u, v, w;
};
vector<node> g;
int p[N];
int n, m;

int find(int y)
{
    if (y == p[y])
        return y;
    return p[y] = find(p[y]);
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < m; i++)
    {
        int a, b, w;
        scanf("%d %d %d" ,&a, &b,&w);
        g.push_back({a, b, w});
    }
    sort(g.begin(), g.end(), [](node a, node b)
         { return a.w < b.w; });

    long long ans = 0, cnt = 0;
    for (int i = 1; i <= n; i++)
        p[i] = i;

    for (int i = 0; i < m; i++)
    {
        int u = g[i].u, v = g[i].v, w = g[i].w;

        u = find(u), v = find(v);
        if (u != v)
        {
            p[u] = v;
            ans += w;
            cnt++;
        }
        if (cnt == n - 1)
            break;
    }
    cout << ans;
    return 0;
}