有关数据存储

类型转换

首先  我们已经了解了部分数据类型在内存中的空间占用 ，以及排列方式。

比如 int 占用 4个字节  首位代表符号位。

那么强制类型转换后 会发生什么？  会得到什么？

让我们举个例子

char a = -1;
signed char b = -1;
unsigned char c = -1;
printf("a = %d,b = %d,c = %d",a,b,c);

这个代码输出的 a b c 的值为多少？

让我们逐个剖析

首先我们来看 a

我们已经知道 a 的值为 - 1； - 1是一个整数

在二进制中 

原码为  10000000 00000000 00000000 00000001

反码为  11111111 11111111 11111111 11111110

补码为  11111111 11111111 11111111 11111111

但是  char 类型只能存放一个字节  也就是8个比特位

在小端存储的vs中 只能获得低数位的1个字节，也就是末尾的 11111111

但打印时用了 %d ，又一次转换为了整形。所以我们要进行整形提升。

我们的符号位不变 向前补1 得到补码

11111111 11111111 11111111 11111111

结果依旧是   -1

然后我们再来看看 b

 signed char b 是一个有符号类型的字符

所以和char b 相同为 - 1

 那么 c 呢？

unsigned char c 说明他是个无符号类型，和前者有一定的区别

让我们分析一下

首先 char 依旧只能拿到 11111111 的二进制位 

但因为首位不再代表符号位，在转换为整形的时候不再向前补1，而是补0。

也就是 00000000 00000000 00000000 11111111

得到的值为 255

-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-

那我们看看下一个例子

char a = -128;
printf("%u",a);

提示：%u 为打印无符号类型的值整数。

我们来分析一下

首先我们要先拿到 - 128的二进制位（10000000 00000000 00000000 10000000）

转换为反码 11111111 11111111 11111111 01111111

转换为补码 11111111 11111111 11111111 1000000

但我们存储在char中的时候  只能存储8个比特位 也就是一个字节，所以

char a 所拿到的二进制位是 10000000。

但我们在打印的时候  依旧是打印了一个整数，所以还是要进行整形提升。

首位字符位为1 我们向前补1  得到补码

11111111 11111111 11111111 10000000

但是  我们注意  我们打印的形式虽然都是整形 但%u代表的是一个无符号的整形，也就是说首位不在代表符号位，而是被视为一个进位。 所以我们会打印一个十分巨大的数字

 那我们进行加减运算的时候又会发生什么呢？

老规矩 举个例子（铁懒狗了）

int i = -20;
unsigned int j = 10;
printf("%d\n",i+j);

我们对这个题目分析一下

首先  i 是一个整形  他的二进制位中

原码为 10000000 00000000 00000000 00010100

反码为 11111111 11111111 11111111 11101011

补码为 11111111 11111111 11111111 11101100

j 也是一个整形  但是一个无符号类型

在二进制位中

原码为 00000000 00000000 00000000 00001010

正数的原码反码补码均相同

然后我们让两个数相加  两个数相加的理论还是一样的 没有变化

11111111 11111111 11111111 11101100

+

00000000 00000000 00000000 00001010

=

11111111 11111111 11111111 11110110

转换为原码即为

10000000 00000000 00000000 00001001

我们打印的是一个 %d 形式的有符号整形

即  结果为 -10

有关浮点数

那么我们浮点数是怎么保存在二进制位中的呢？

首先 我们用单精度浮点型 float 来举例

 已知一个数   5.5

那么他是怎么存储的呢？

我们知道5的二进制位是 101  那是不是代表  存储的值就是 101.101呢？

其实不是

在小数点后面的位 存储的方式有些变化  他们不再是2的正数次方  而是负数次。

也就是说 小数点后面的5其实是 2的-1次方，即  0.5

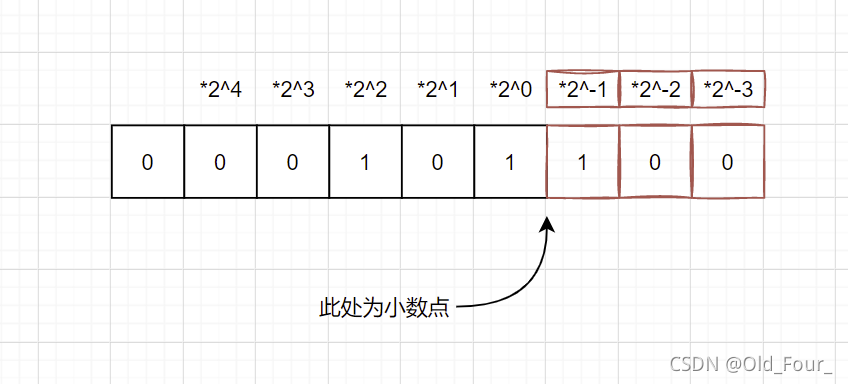
 所以我们暂时把他们认作为 ==>    101.1

我们知道十进制中  110.5可以写作为  1.105*10^2

二进制当中也是一样     101.1可以转换成（M） 1.011*^2 （E）

用首位S来存储符号位，记录方式为   (-1)*^S   

当S为1 则整个数值就会 乘 -1，即为负数，当S=0，则为正数。

这里我们做出总结 

浮点数的存储思路为（-1)^S  * M * 2^E

(-1)^表示符号位  M为有效数字  2^E表示指数位

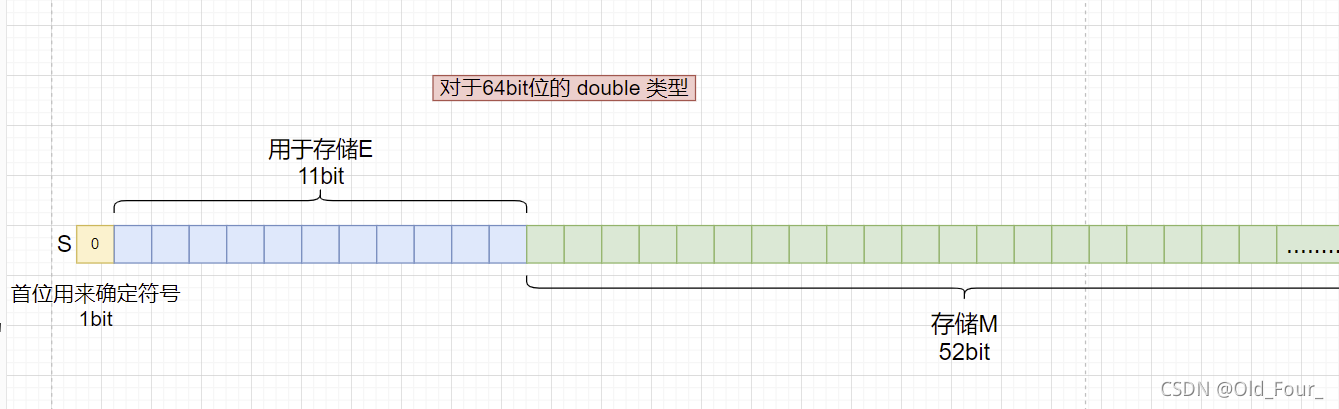
那么这些数怎么存储在二进制中的呢？如何摆放？

如下图所示：

 不过先别急着下定论

我们发现 二进制条件下 M 的值小数点前一位一定是1，所以我们将其省略并默认为1，

这样就节约了一个比特位的空间  ，精度更高！

现在 我们知道了如何存放S 和 M。

那么E又是怎么存放的呢？

首先E 是一个无符号数，然而有些时候 E 可能为负数，那怎么办呢？

在这里  IEEE 754 规定  E 在存放的时候  要在原有的数值基础上  增加127以进行修正，  并把得到的值存入 E

在双精度浮点数中  存放方式相同 进保存的位数不同，且增加的补正值有所区别

float类型中  分配给E的空间为11bit  M 为52bit  ，且补正值为1023.

 那我既然将浮点数存在了内存中，那要如何读取？

这里我们分三种情况

E既不为全0，也不为全1

这里我们便正常流程  取出E的值  减去127或1023的修正值 得到真实值，在M中取出数据 在小数点前补一个1，通过公式计算  得到浮点数的值

E为全0

这个时候 会被视为E = 1-127或 1-102。用来表示一个非常非常小的数，无限接近于±0的数字。

E为全1

这个时候 数字会变得非常非常大，如果有效数字M = 0，表示±无穷大（正负取决于符号位S）