正则化
一、正则化的线性回归模型
1.成本函数
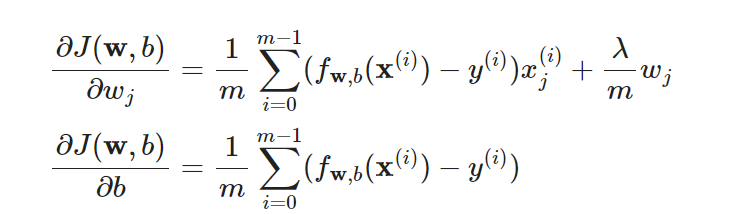
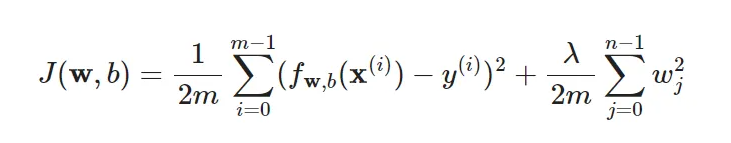
def compute_cost(X, y, w, b, lambda_):
m = X.shape[0]
n = len(w)
cost = 0.
for i in range(m):
z_i = np.dot(X[i], w) + b
cost += (z_i - y[i]) ** 2
cost = cost / (2 * m)
reg_cost = 0
for j in range(n):
reg_cost += w[j] ** 2
reg_cost = (lambda_ / (2 * m)) * reg_cost
return cost + reg_cost
2.梯度下降函数
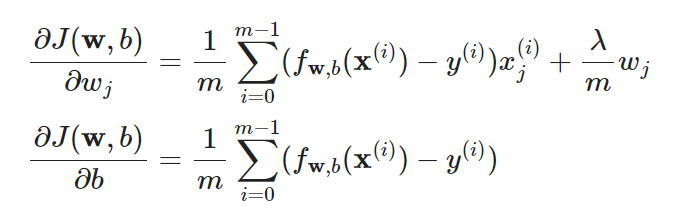
二、正则化的逻辑回归模型
1.成本函数
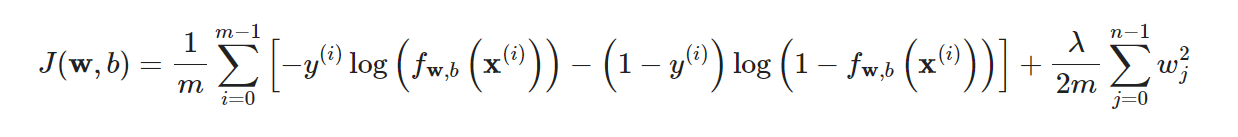
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def compute_cost(X, y, w, b, lambda_):
m = X.shape[0]
n = len(w)
cost = 0.
for i in range(m):
z_i = np.dot(X, w) + b
f_wb_i = sigmoid(z_i)
cost += y[i] * np.log(f_wb_i) + (1 - y[i]) * np.log(1 - f_wb_i)
cost = cost / (-m)
reg_cost = 0
for j in range(n):
reg_cost += w[j] ** 2
reg_cost = (lambda_ / (2 * m)) * reg_cost
return cost + reg_cost
2.梯度下降函数
def compute_gradient(X, y, w, b, lambda_):
m, n = X.shape[0]
df_dw = np.zeros((n,))
df_db = 0.0
for i in range(m):
z_i = np.dot(X, w) + b
f_wb_i = sigmoid(z_i)
err = f_wb_i - y[i]
for j in range(m):
df_dw[j] += err * X[i, j]
df_db += err
df_dw = df_dw / m
df_db = df_db / m
for j in range(n):
df_dw[j] = df_dw[j] + (lambda_ / m) * w[j]
return df_dw, df_db
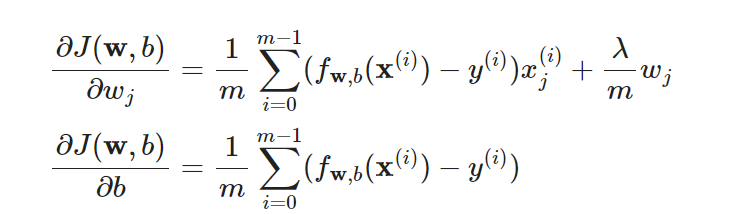
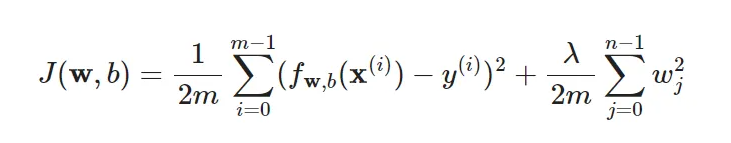
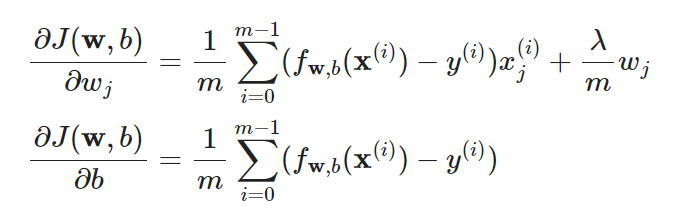
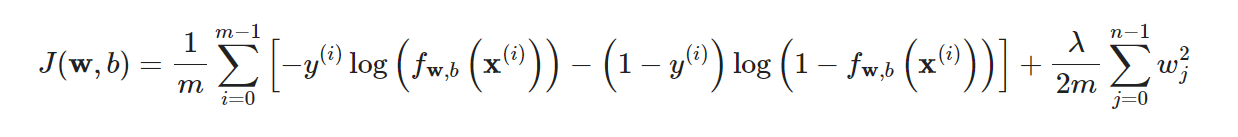
 正则化线性与逻辑回归详解
正则化线性与逻辑回归详解























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










