人工智能 --- 吉布斯采样

      贝叶斯网络如下图所示，包含 4 个随机变量，每个变量都只有表示是否的两个值。请用吉布斯采样方法回答以下问题。 

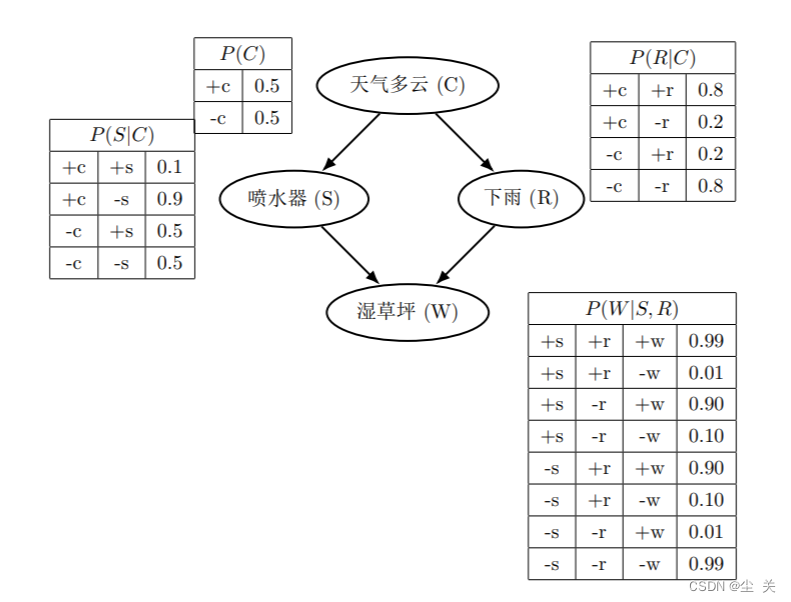
假设观察到 𝑅 = +𝑟, 初始化样本中其他变量的赋值为 𝐶 = +𝑐, 𝑆 = −𝑠, 𝑊 = −𝑤。

1). 假设随机采样变量是 S，随机数是 0.235，请计算 S 的值，并给出此时的状态样本值。

2). 假设下一个采样的变量是 C，随机数是 0.625，请计算这一步采样后的状态样本是什么。 

答：

1）对后验概率分布 𝑃 (𝑆| − 𝑤, +𝑟, +𝑐) 进行随机采样。

𝑃(𝑆| − 𝑤, +𝑟, +𝑐) = 1/ 𝑍  𝑃(𝑆, −𝑤| + 𝑟, +𝑐) 𝑃(𝑆, −𝑤| + 𝑟, +𝑐) =𝑃 (𝑆| + 𝑐, +𝑟)𝑃 (−𝑤|𝑆, +𝑐, +𝑟)

   由   条件独立性   可得                   =𝑃 (𝑆| + 𝑐)𝑃 (−𝑤|𝑆, +𝑟)

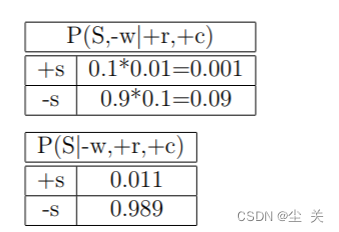
根据上面的分布，随机数 0.235 将落在 −𝑠 的区间，所以，𝑆 = −𝑠，此时的样本为 +𝑐, −𝑠, +𝑟, −𝑤。

   你算概率出来，拿随机数跟概率相比，就知道它落在那块区域了。

2) 从分布 𝑃 (𝐶| − 𝑠, +𝑟, −𝑤) 中对变量 𝐶 进行采样。

𝑃(𝐶| − 𝑠, +𝑟, −𝑤) =𝑃 (𝐶| − 𝑠, +𝑟) 条件独立 = 1/ 𝑍 𝑃 (𝐶, +𝑟, −𝑠) 𝑃(𝐶, +𝑟, −𝑠) =𝑃 (𝐶, +𝑟)𝑃 (−𝑠, |𝐶, +𝑟) 由条件独立可得    =𝑃(𝐶)𝑃 (+𝑟|𝐶)𝑃 (−𝑠|𝐶)

 根据上面的分布，随机数 0.625 应该落在 +𝑐 的区间，所以此时 𝐶 = +𝑐，相应的样本值 是 +𝑐, −𝑠, +𝑟, −𝑤。