文章目录
3.5一个活动编辑的最迟开始时间编辑和其最早开始时间编辑的差额
图的应用
本节是历年考查的重点。图的应用主要包括:最小生成(代价)树、最短路径、拓扑排序和关键路径。
一般而言,这部分内容直接以算法设计题形式考查的可能性极小,而更多的是结合图的实例来考查算法的具体操作过程,读者必须学会手工模拟给定图的各个算法的执行过程。
此外,还需掌握对给定模型建立相应的图去解决问题的方法。
考纲内容
(一)图的基本概念
(二)图的存储及基本操作
邻接矩阵;邻接表;邻接多重表;十字链表
(三)图的遍历
深度优先搜索;广度优先搜索
(四)图的基本应用
最小(代价)生成树;最短路径;拓扑排序;关键路径
复习提示
图算法的难度较大,主要掌握深度优先搜索与广度优先搜索。掌握图的基本概念及基本性质、图的存储结构(邻接矩阵、邻接表、邻接多重表和十字链表)及特性、存储结构之间的转化、基于存储结构上的各种遍历操作和各种应用(拓扑排序、最小生成树、最短路径和关键路径)等。
图的相关算法较多,通常只需掌握其基本思想和实现步骤,而实现代码不是重点。
1.有向无环图描述表达式
有向无环图:若一个有向图中不存在环,则称为有向无环图,简称DAG图。
【命题追踪——构建表达式的有向无环图】
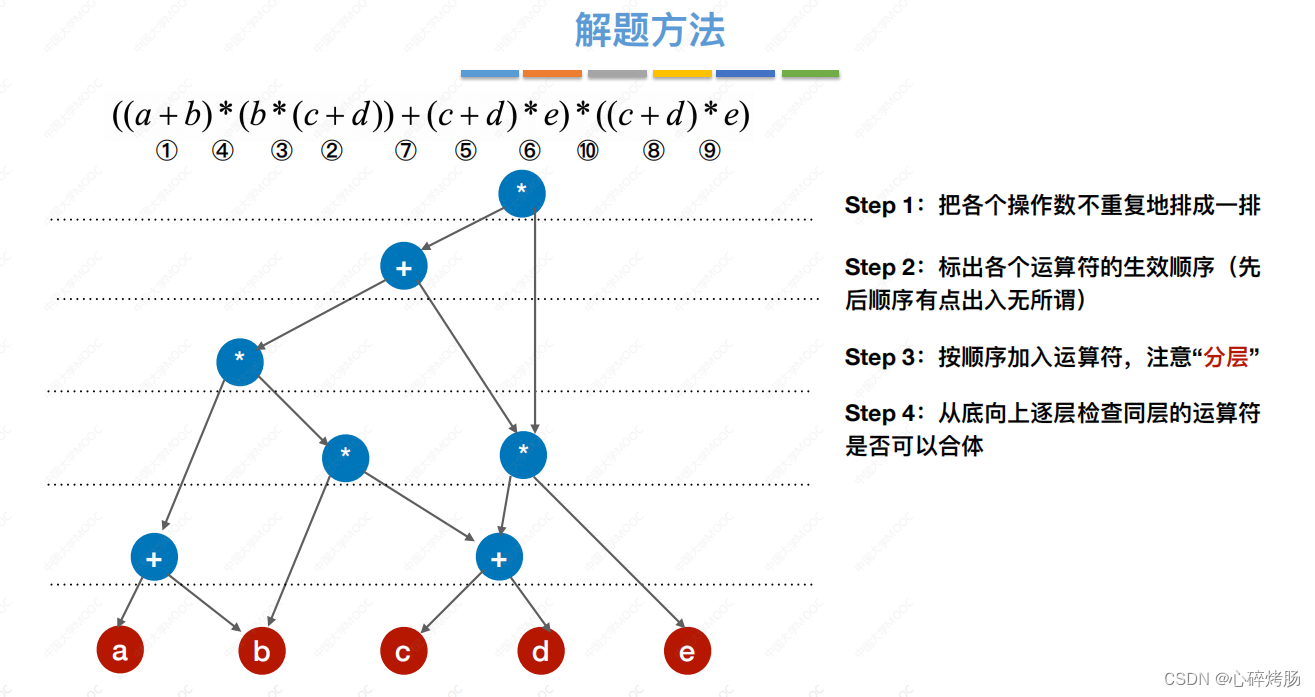
有向无环图是描述含有公共子式的表达式的有效工具。例如表达式
((a+b)*(b*(c+d))+(c+d)*e)*((c+d)*e)
可以用上一章描述的二叉树来表示,如图6.20所示。
仔细观察该表达式,可发现有一些相同的子表达式(c+d)和(c+d)*e,而在二叉树中,它们也重复出现。
若利用有向无环图,则可实现对相同子式的共享,从而节省存储空间,图6.21所示为该表达式的有向无环图表示。
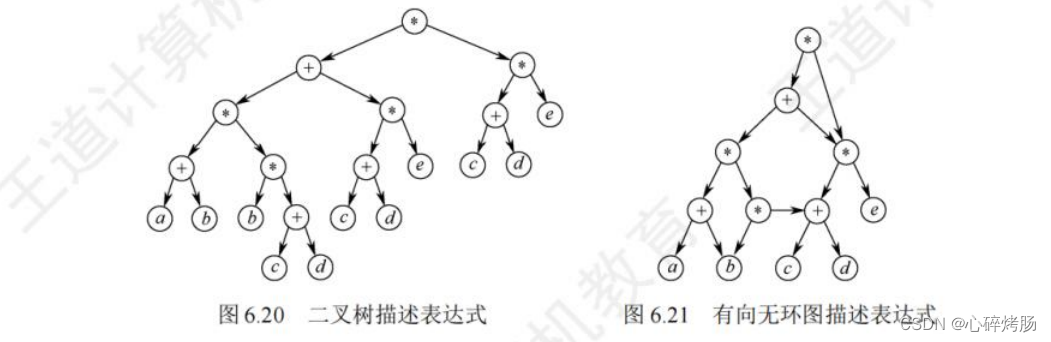
注意:在表达式的有向无环图表示中,不可能出现重复的操作数顶点
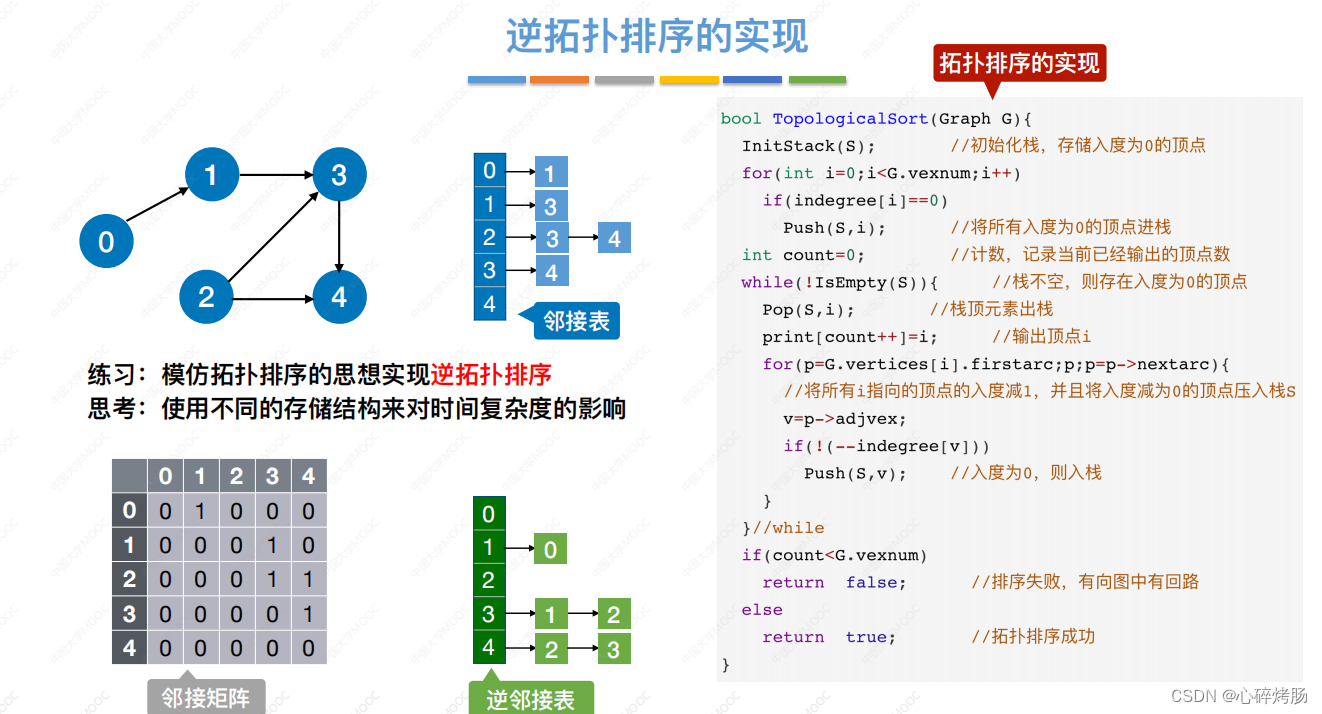
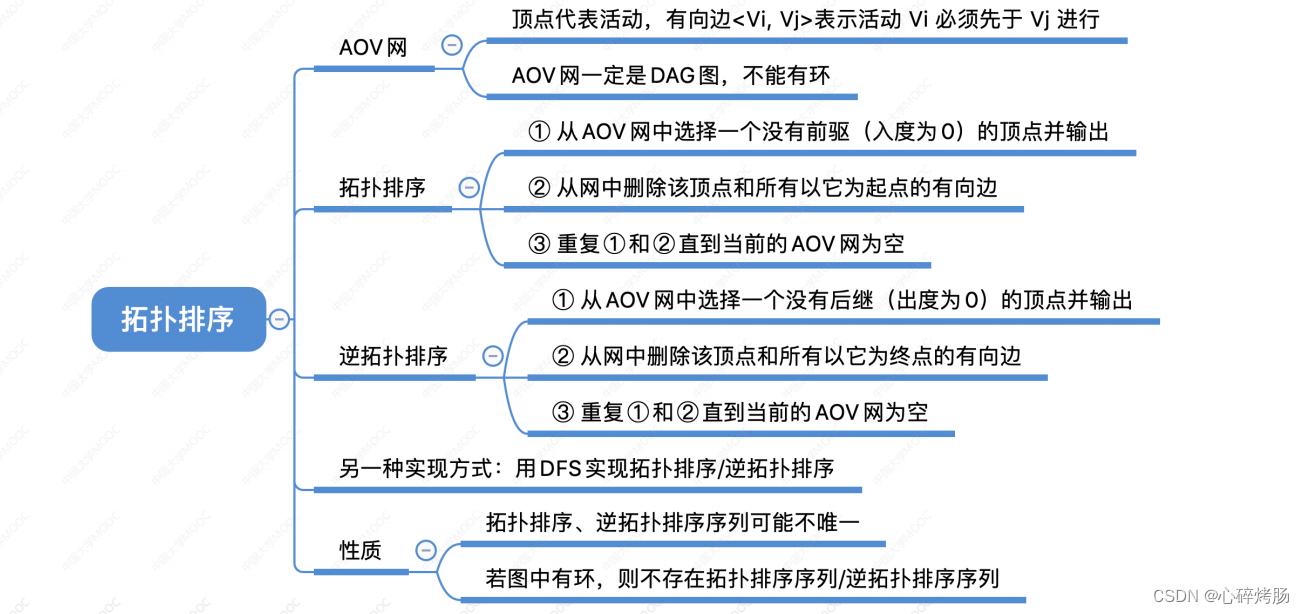
2.拓扑排序
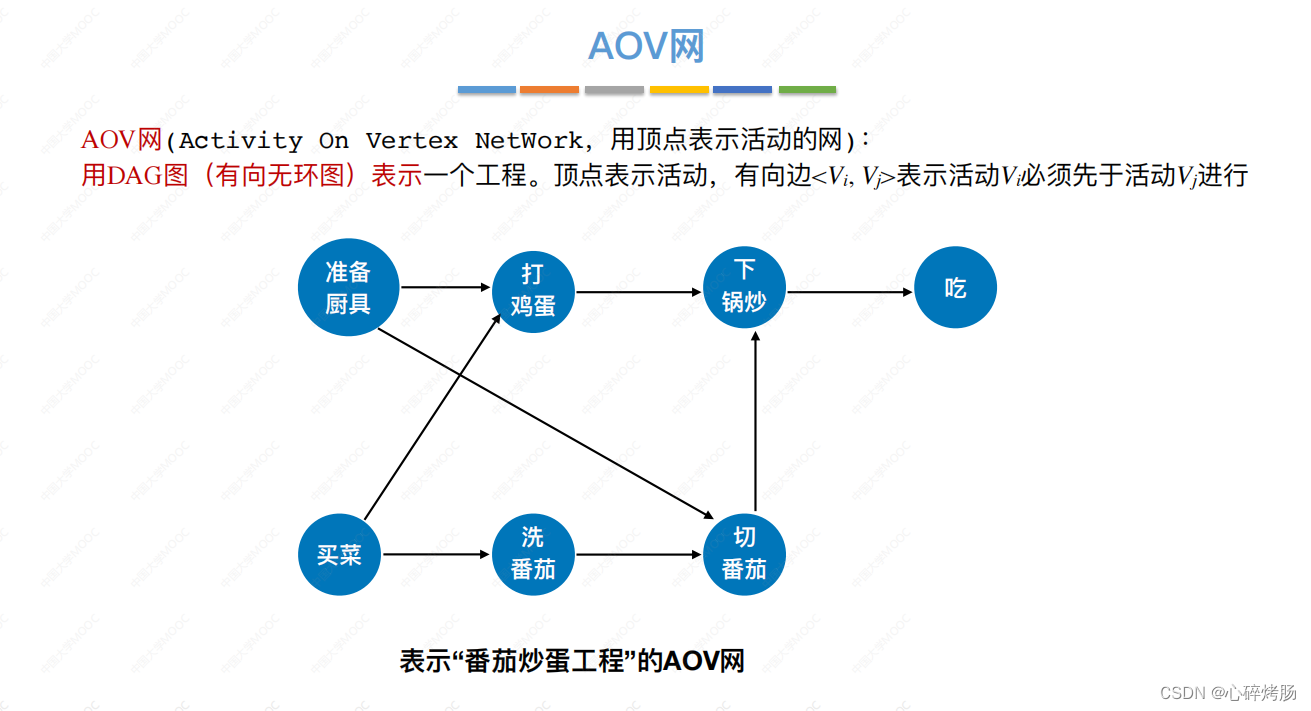
AOV网:若用有向无环图表示一个工程,其顶点表示活动,用有向边<Vi,Vj>表示活动Vi必须先于活动Vj进行的这样一种关系,则将这种有向图称为顶点表示活动的网络,简称 AOV 网。
在 AOV网中,活动Vi是活动Vj的直接前驱,Vj是Vi的直接后继,这种前驱和后继关系具有传递性,且任何活动Vi不能以它自己作为自己的前驱或后继。
拓扑排序:在图论中,由一个有向无环图的顶点组成的序列,当且仅当满足下列条件时,称为该图的一个拓扑排序:
1) 每个顶点出现且只出现一次。
2) 若顶点A在序列中排在顶点B的前面,则在图中不存在从B到A的路径。
或定义为:拓扑排序是对有向无环图的顶点的一种排序,它使得若存在一条从顶点A到顶点B的路径,则在排序中B出现在A的后面。
每个AOV网都有一个或多个拓扑排序序列。

【命题追踪——拓扑排序和回路的关系】
对一个 AOV 网进行拓扑排序的算法有很多,下面介绍比较常用的一种方法的步骤:
① 从 AOV 网中选择一个没有前驱(入度为 0)的顶点并输出。
② 从网中删除该顶点和所有以它为起点的有向边。
重复①和②直到当前的 AOV 网为空或当前网中不存在无前驱的顶点为止。
后一种情况说明有向图中必然存在环。
【命题追踪——拓扑排序的实例】
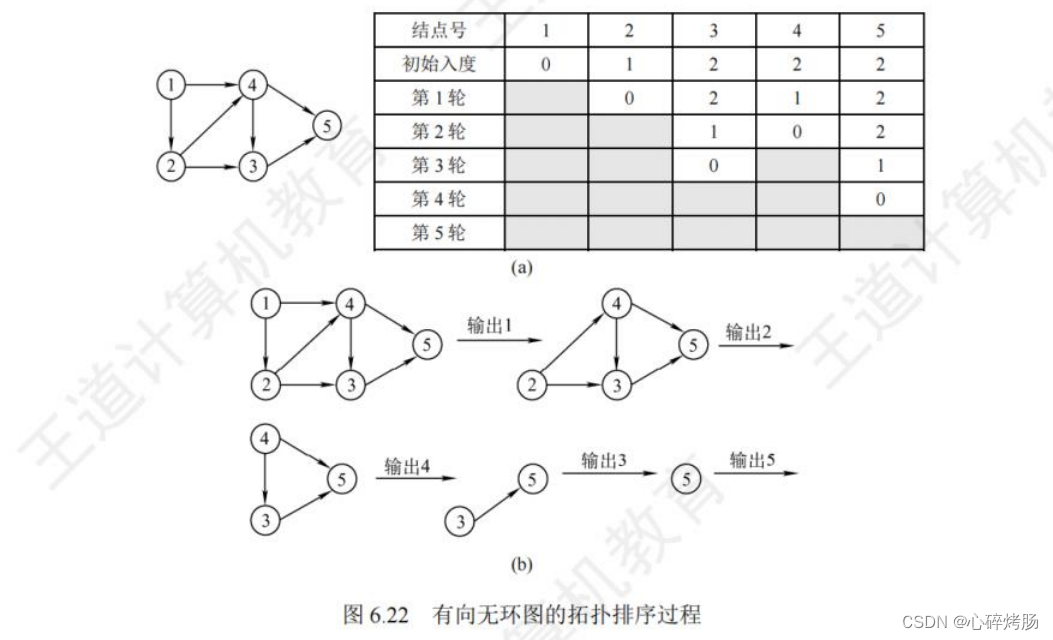
图6.22所示为拓扑排序过程的示例。每轮选择一个入度为0的顶点并输出,然后删除该顶点和所有以它为起点的有向边,最后得到拓扑排序的结果为{1,2,4,3,5}。
拓扑排序算法的实现如下:
bool TopologicalSort(Graph G){
InitStack(S); //初始化栈,存储入度为0的顶点
int i;
for(i=0;i<G.vexnum;i++)
if(indegree[i]==0)
Push(S i); //将所有入度为0的顶点进栈
int count=0; //计数,记录当前已经输出的顶点数
while(!IsEmpty(S)){ //栈不空,则存在入度为0的顶点
Pop(S,i); //栈顶元素出栈
print[count++]=i; //输出顶点i
for(p=G.vertices[i].firstarc;p;p=p->nextarc){
//将所有i指向的顶点的入度减1,并且将入度减为0的顶点压入栈s
v=p->adjvex;
if(!(--indegree[v]))
Push(S,v); //入度为0,则入栈
}
}
if(count<G.vexnum)
return false; //排序失败,有向图中有回路
else
return true; //拓扑排序成功
}
【命题追踪——不同存储方式下的拓扑排序的效率】
因为输出每个顶点的同时还要删除以它为起点的边,
所以采用邻接表存储时拓扑排序的时间复杂度为 O(|V|+|E|),
采用邻接矩阵存储时拓扑排序的时间复杂度为 O(|V|²)。
【命题追踪——DFS 实现拓扑排序的思想】
此外,利用上一节的深度优先遍历也可以实现拓扑排序,下面简单描述其思路。
对于有向无环图G中的任意结点u,v它们之间的关系必然是下列三种之一:
1) 若u是v的祖先,则在调用 DFS 访问 u 之前,必然已对 v 进行了 DFS 访问,即 v 的 DFS结束时间先于 u 的 DFS 结束时间。
从而可考虑在 DFS 函数中设置一个时间标记,在DFS调用结束时,对各顶点计时。
因此,祖先的结束时间必然大于子孙的结束时间。
2) 若u是v的子孙,则v为u的祖先,按上述思路,v的结束时间大于u的结束时间。
3) 若u和v没有路径关系,则u和v在拓扑序列的关系任意。
于是,按结束时间从大到小排列,就可以得到一个拓扑排序序列。
对一个 AOV 网,若采用下列步骤进行排序,则称之为逆拓扑排序:
① 从 AOV 网中选择一个没有后继(出度为 0)的顶点并输出。
② 从网中删除该顶点和所有以它为终点的有向边,
③ 重复①和②直到当前的 AOV 网为空。


用拓扑排序算法处理 AOV 网时,应注意以下问题:
1) 入度为零的顶点,即没有前驱活动的或前驱活动都已经完成的顶点,工程可以从这个顶点所代表的活动开始或继续。
【命题追踪——分析给定图的拓扑序列的存在性和唯一性】
2) 若一个顶点有多个直接后继,则拓扑排序的结果通常不唯一;
但若各个顶点已经排在一个线性有序的序列中,每个顶点有唯一的前驱后继关系,则拓扑排序的结果是唯一的。
3) 由于 AOV 网中各顶点的地位平等,每个顶点编号是人为的,因此可以按拓扑排序的结果重新编号,生成 AOV 网的新的邻接存储矩阵;
这种邻接矩阵可以是三角矩阵;但对于一般的图来说,若其邻接矩阵是三角矩阵,则存在拓扑序列;反之则不一定成立。
3.关键路径
在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销(如完成活动所需的时间),称之为用边表示活动的网络,简称 AOE网。
AOE 网和 AOV 网都是有向无环图,不同之处在于它们的边和顶点所代表的含义是不同的;
AOE 网中的边有权值;
而 AOV 网中的边无权值,仅表示顶点之间的前后关系。
AOE 网具有以下两个性质:
① 只有在某顶点所代表的事件发生后,从该顶点出发的各有向边所代表的活动才能开始;
② 只有在进入某顶点的各有向边所代表的活动都已结束时,该顶点所代表的事件才能发生。
在 AOE 网中仅有一个入度为0的顶点,称为开始顶点(源点),它表示整个工程的开始;
也仅有一个出度为0的顶点,称为结束顶点(汇点),它表示整个工程的结束。
【命题追踪——关键路径的性质】
在 AOE 网中,有些活动是可以并行进行的。从源点到汇点的有向路径可能有多条,并且这些路径长度可能不同。
完成不同路径上的活动所需的时间虽然不同,但是只有所有路径上的活动都已完成,整个工程才能算结束。
因此,从源点到汇点的所有路径中,具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动。
完成整个工程的最短时间就是关键路径的长度,即关键路径上各活动花费开销的总和。
这是因为关键活动影响了整个工程的时间,即若关键活动不能按时完成,则整个工程的完成时间就会延长。
因此,只要找到了关键活动,就找到了关键路径,也就可以得出最短完成时间。
下面给出在寻找关键活动时所用到的几个参量的定义。
3.1事件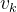 的最早发生时间
的最早发生时间
它是指从源点到顶点
的最长路径长度。事件
的最早发生时间决定了所有从
开始的活动能够开工的最早时间。
可用下面的递推公式来计算:
(源点)=0
,
为
的任意后继,
表示
上的权值
注意:
计算
值时,按从前往后的顺序进行,可以在拓扑排序的基础上计算:
① 初始时,令。
② 输出一个入度为0的顶点时,计算它所有直接后继顶点
的最早发生时间,若
,
则
。以此类推,直至输出全部顶点。
3.2事件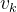 的最迟发生时间
的最迟发生时间
它是指在不推迟整个工程完成的前提下,即保证它的后继事件在其最迟发生时间
能够发生时,该事件最迟必须发生的时间。
可用下面的递推公式来计算:
(汇点)=
(汇点)
,
为
的任意前驱
注意:
计算值
时,按从后往前的顺序进行,可以在逆拓扑排序的基础上计算。
增设一个栈以记录拓扑序列,拓扑排序结束后从栈顶至栈底便为逆拓扑有序序列。
过程如下:
① 初始时,令。
② 栈顶顶点出栈,计算其所有直接前驱顶点
的最迟发生时间,若
,
则
。以此类推,直至输出全部栈中顶点。
3.3活动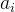 的最早开始时间
的最早开始时间
它是指该活动弧的起点所表示的事件的最早发生时间。若边表示活动
,则有
3.4活动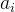 的最迟开始时间
的最迟开始时间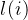
它是指该活动弧的终点所表示事件的最迟发生时间与该活动所需时间之差。若边表示活动
,则有
。
3.5一个活动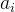 的最迟开始时间
的最迟开始时间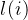 和其最早开始时间
和其最早开始时间 的差额
的差额
它是指该活动完成的时间余量,即在不增加完成整个工程所需总时间的情况下,活动可以拖延的时间。
若一个活动的时间余量为零,则说明该活动必须要如期完成,否则就会拖延整个工程的进度,所以称即
的活动
是关键活动。
【命题追踪——求关键路径的实例】
求关键路径的算法步骤如下:
① 从源点出发,令(源点)=0,按拓扑有序求其余顶点的最早发生时间
。
② 从汇点出发,令 (汇点)=
(汇点),按逆拓扑有序求其余顶点的最迟发生时间
。
③ 根据各顶点的值求所有弧的最早开始时间
。
④ 根据各顶点的值求所有弧的最迟开始时间
。
⑤ 求 AOE 网中所有活动的差额,找出所有
的活动构成关键路径
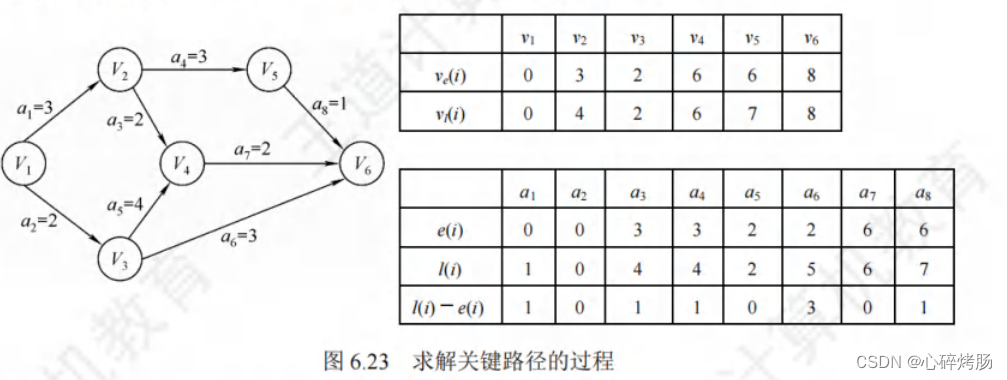
图 6.23 所示为求解关键路径的过程,简单说明如下:
① 求:初始
,在拓扑排序输出顶点过程中,求得
,
,
,
,
若这是一道选择题,根据上述求的过程就已经能知道关键路径。
② 求:初始
,在逆拓扑排序出栈过程中,求得
,
,
必然为0而无须再求。
③ 弧的最早开始时间等于该弧的起点的顶点的
,结果如下表。
④ 弧的最迟开始时间等于该弧的终点的顶点的
减去该弧持续的时间,结果如下表。
⑤ 根据的关键活动,得到的关键路径为(v1,v3,v4,v6)。
【命题追踪——缩短工期的相关分析】
对于关键路径,需要注意以下几点:
1) 关键路径上的所有活动都是关键活动,它是决定整个工程的关键因素,因此可以通过加快关键活动来缩短整个工程的工期。
但也不能任意缩短关键活动,因为一旦缩短到一定的程度,该关键活动就可能会变成非关键活动。
2) 网中的关键路径并不唯一,且对于有几条关键路径的网,只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。
各种图算法在采用邻接矩阵或邻接表存储时的时间复杂度如表 6.5 所示。

4.知识回顾
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










