原码，反码，补码，移码

原码,补码,反码，移码：

首先清楚为什么会出现这四种编码表示方式？在我看来因为计算机底层本身不能像人类那样直接识别算术运算符+-*/，因为计算机中一般都是采用二进制数来表示数据，所以为了计算机能够以0/1就能进行这些算术运算，从而出现了这几种编码表达式。以下内容都是围绕二进制数展开讨论的。

原码：

不论二进制数是正数还是负数原码的数值位都与二进制数的数值相同。

（这里假设机器长度为5位）

纯小数型：符号位+小数位. 如：二进制数-0.1101 的原码为 1.1101

纯整数型：符号位+整数位 如：二进制数-1011 的原码为 11011

符号位一般用0表示整数，用1表示负数。

注意在原码中，若二进制数为0，则有两种表示形式

+0的原码为00000

-0的原码为10000

原码表示法的优点：直观易懂，用来进行乘除运算时较为简单。

缺点：不方便进行加减运算。

反码：

若二进制数为正数，则该二进制数的反码与原码相同。

如： 二进制数1111 原码为 01111 反码为01111

若二进制数为负数，则该二进制数的反码的符号位与原码相同，数值位与原码相反。

如： 二进制数-1100 原码为11100 反码为 10011

小数位同理。

需要注意的是反码中的0也是有两种表现形式：

+0的反码为 01111

-0的反码为 11111

补码：

若二进制数为正数，则该二进制数的补码与原码相同。

如： 二进制数1111 原码为 01111 反码为01111 补码为01111

若二进制数为负数，则该二进制数的补码的符号位与原码相同，数值位为反码+1。

如： 二进制数-1100 原码为11100 反码为 10011 补码为 10100

 

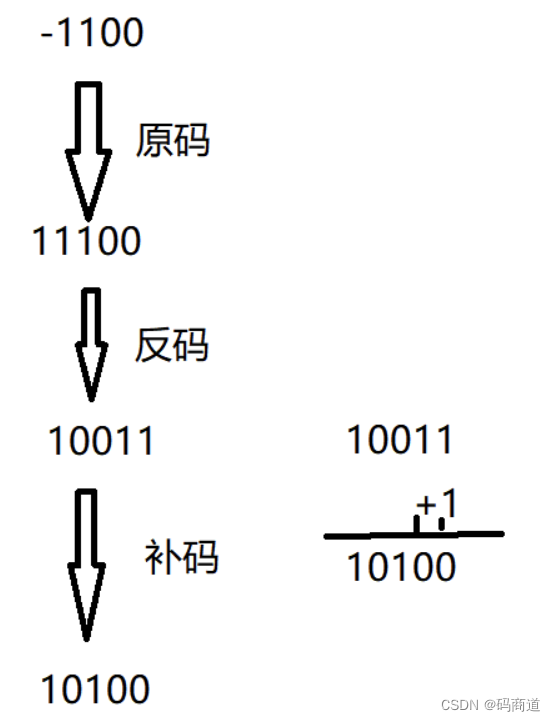
小数位同理。

优点：

1、用加法就可以实现减法、乘法和除法运算，能简化计算机中运算器的内部结构。

2、可以让符号位作为数值直接参加运算，而最后仍然可以得到正确的结果符

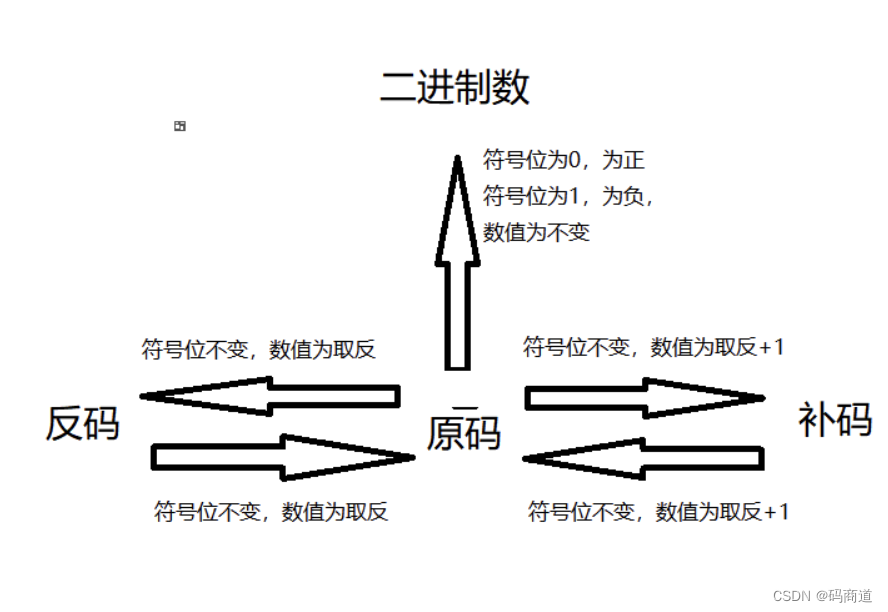
原码，补码，反码之间的相互转换：

 

移码：

又称为增码或者偏码

组成： 偏移值+数值

假设偏移值为2^7,二进制数为字长为8位的纯整数型（定点整数）

则二进制数11011111的移码为111011111（既100000000+11011111）

主要用于表示浮点数的阶码部分。(具体请看浮点数的表示方法)

练习：

二进制数	原码	反码	补码
1011	01101	01101	01101
-1011	11011	10100	10101
0.1110	0.1110	0.1110	0.1110
-0.1110	1.1110	1.0001	1.0010