概率 + 统计大数定律与中心极限定理（五）

最新推荐文章于 2024-01-05 16:00:05 发布

一杯敬朝阳一杯敬月光

最新推荐文章于 2024-01-05 16:00:05 发布

阅读量566

点赞数

分类专栏：笔记文章标签：笔记

本文链接：https://blog.csdn.net/qq_xuanshuang/article/details/107306451

版权

笔记专栏收录该内容

14 篇文章 1 订阅

订阅专栏

大数定律

切比雪夫不等式

设随机变量X具有数学期望 $E(X)=\mu$ ，方差 $D(X) = \sigma^2$ ，则对于任意正数 $\epsilon$ ，有不等式

$\begin{aligned} &P\{|X-E(X)| \geqslant \epsilon\} \leqslant \frac{\sigma^2}{\epsilon^2}\\ or \ &P\{|X-E(X)|< \epsilon\} \geqslant 1 - \frac{\sigma^2}{\epsilon^2} \end{aligned}$

由切比雪夫不等式可以看出，若 $\sigma$ 越小，则事件 $\{|X-E(X)|< \epsilon\}$ 的概率越大，即随机变量X 集中在期望附近的可能性越大.

大数定律的客观背景

设 $Y_1,Y_2,\cdots,Y_n,\cdots$ 是一个随机变量序列，a是一个常数，若对于任意正数 $\epsilon$ ，有 $\lim_{n\rightarrow \infty}P\{|Y_n-a| < \epsilon\}=1$ ，则称序列 $Y_1,Y_2,\cdots,Y_n,\cdots$ 依概率收敛于a，记作 $Y_n \overset{P}{\rightarrow} a$ 。

性质：设 $X_n \overset{P}{\rightarrow} a$ ， $Y_n \overset{P}{\rightarrow} b$ ，又设函数g(X,Y)在点(a,b)连续，则 $g(X_n,Y_n) \overset{P}{\rightarrow} g(a,b)$ 。

切比雪夫大数定律：

设 $X_1,X_2,\cdots,X_n,\cdots$ 是一个随机变量序列，如果存在常数C，使得 $D(X_k) \leqslant C(k=1,2,\cdots)$ ，则对于任意正数 $\epsilon$ 有 $\lim_{n \rightarrow \infty}P\{|\frac{1}{n}\sum_{k=1}^nX_k - \frac{1}{n}\sum_{k=1}^nE(X_k)| < \epsilon\} = 1$ ，也就是说 $\frac{1}{n}\sum_{k=1}^nX_k \overset{P}{\rightarrow} \frac{1}{n}\sum_{k=1}^nE(X_k)$ 。

贝努利大数定律

设 $n_A$ 是n次独立重复试验中事件A发生的次数，p是事件A在每次试验中发生的概率，则对于任意任意正数 $\epsilon$ ，有

$\begin{aligned} &\lim_{n \rightarrow \infty}P\{|\frac{n_A}{n}| < \epsilon\} = 1 \\ or \ &\lim_{n \rightarrow \infty}P\{|\frac{n_A}{n}| \geqslant \epsilon\} = 0 \end{aligned}$ ，也就是说 $\frac{n_A}{n} \overset{P}{\rightarrow} p$

在实际应用中，当试验次数很大时，就可以用事件的频率来代替事件的概率。

辛钦大数定律

设 $X_1,X_2,\cdots,X_n,\cdots$ 是相互独立，服从同一分布的随机变量序列，且具有数学期望 $E(X_k)=\mu (k=1,2,\cdots)$ 。则对于任意正数 $\epsilon$ ，有 $\lim_{n \rightarrow \infty}P\{|\frac{1}{n}\sum_{k=1}^nX_k - \mu| < \epsilon\} = 1$ ，也就是说 $\frac{1}{n}\sum_{k=1}^nX_k \overset{P}{\rightarrow} \mu$

中心极限定理

中心极限定理的客观背景：在客观实际中，许多随机变量是由大量的相互独立的随机因素的综合影响所形成的。而其中每一个别因素所起的作用都是微小的。这样的随机变量往往近似地服从正态分布！

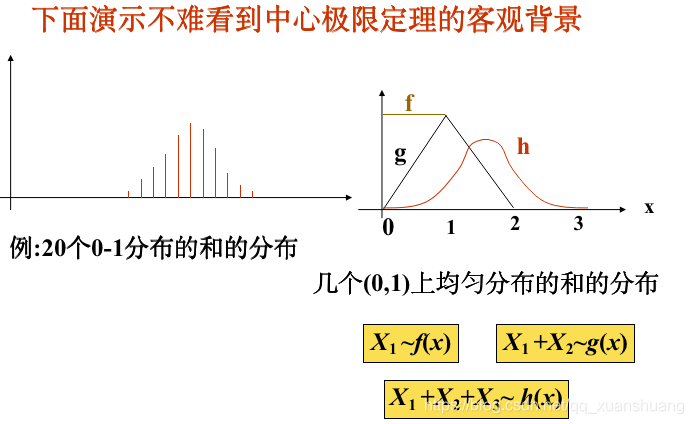
中心极限定理

定理1（独立同分布情形下的中心极限定理）设随机变量 $X_1,X_2,\cdots,X_n,\cdots$ 相互独立，服从同一分布，具有数学期望和方差， $E(X_k) = \mu, D(X_k) = \sigma^2(k=1,2,\cdots)$ ，则随机变量值和 $\sum_{k=1}^nX_k$ 的标准化变量 $Y_n = \frac{\sum_{k=1}^nX_k - n \mu}{\sqrt{n}\sigma}$ 的分布函数 $F_n(x)$ 对于任意x满足 $\lim_{n \rightarrow \infty}F_n(x) = \lim_{n \rightarrow \infty}P\{ \frac{\sum_{k=1}^nX_k - n \mu}{\sqrt{n}\sigma}\leqslant x\}=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-t^2/2}dt = \varnothing(x)$

定理2（德莫佛－拉普拉斯中心极限定理）: 设随机变量 $(\Lambda _n, n =1,2,\cdots)$ 服从参数n,p(0<p<1)的二项分布，则对任意x，有

$\lim_{n \rightarrow \infty}P\{ \frac{\Lambda_n - n p}{\sqrt{np(1-p)}}\leqslant x\}=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-t^2/2}dt = \varnothing(x)$

定理表明：二项分布的极限分布是正态分布，即

定理3（李雅普诺夫中心极限定理）设随机变量 $X_1,X_2,\cdots,X_n,\cdots$ 相互独立，具有数学期望和方差 $E(X_k) = \mu_k, D(X_k) = \sigma_k^2(k=1,2,\cdots)$ ，记 $B_n^2 = \sum_{k=1}^{n}\sigma_k^2$ ，若存在正数 $\delta$ ，使得当 $n\rightarrow +\infty$ 时，

$\frac{1}{B_n^{2+\delta}}\sum_{k=1}^n E\{|X_k - \mu_k|^{2+\delta}\} \rightarrow 0$ ，则随机变量值和 $\sum_{k=1}^nX_k$ 的标准化量 $Z_n = \frac{\sum_{k=1}^nX_k - E(\sum_{k=1}^nX_k)}{\sqrt{D(\sum_{k=1}^nX_k)}}=\frac{\sum_{k=1}^nX_k-\sum_{k=1}^n\mu_k}{B_n}$ 的分布函数 $F_n(x)$ 对于任意x，满足 $lim_{n\rightarrow \infty}F_n(x) =\{\frac{\sum_{k=1}^nX_k-\sum_{k=1}^n\mu_k}{B_n} \leqslant x\}=\int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}e^{-t^2/2}dt = \varnothing(x)$

一杯敬朝阳一杯敬月光

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
概率 + 统计大数定律与中心极限定理（五）

大数定律切比雪夫不等式设随机变量X具有数学期望，方差，则对于任意正数，有不等式由切比雪夫不等式可以看出，若越小，则事件的概率越大，即随机变量X 集中在期望附近的可能性越大.大数定律的客观背景设是一个随机变量序列，a是一个常数，若对于任意正数，有，则称序列依概率收敛于a，记作。性质：设，，又设函数g(X,Y)在点(a,b)连续，则。切比雪夫大数定律：设是一个随机变量序列，如果存在常数C，使得，则对于任意正数有，也就是说。贝努利大数定律设是n次独立...
复制链接

扫一扫