树的初阶相关知识(下）

   https://blog.csdn.net/qscftqwe/article/details/155913703

        这是上节课的知识，大家可以点进去看一下！

一.复盘树的初阶相关知识（上）的题目

1.下列关键字序列为堆的是：（）
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32

2.已知小根堆为8,15,10,21,34,16,12，删除关键字 8 之后需重建堆，在此过程中
关键字之间的比较次数是（）。
A 1
B 2
C 3
D 4

3.一组记录排序码为(5 11 7 2 3 17),则利用堆排序方法建立的初始堆为
A(11 5 7 2 3 17)
B(11 5 7 2 17 3)
C(17 11 7 2 3 5)
D(17 11 7 5 3 2)
E(17 7 11 3 5 2)
F(17 7 11 3 2 5)

4.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后，其结果是（）
A[3，2，5，7，4，6，8]
B[2，3，5，7，4，6，8]
C[2，3，4，5，7，8，6]
D[2，3，4，5，6，7，8]






1.A
2.C
3.C
4.C

        通过上节课的知识，我们就能轻松把这几题搞定，如果做不出来你可以去看看我上节课的内容，那个对堆的理解有很大的帮助！

二.建堆时间复杂度

        当我们学习这个，我们就知道为什么建堆采用的是向下建堆而不是向上建堆！

        因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个节点不影响最终结果)

​

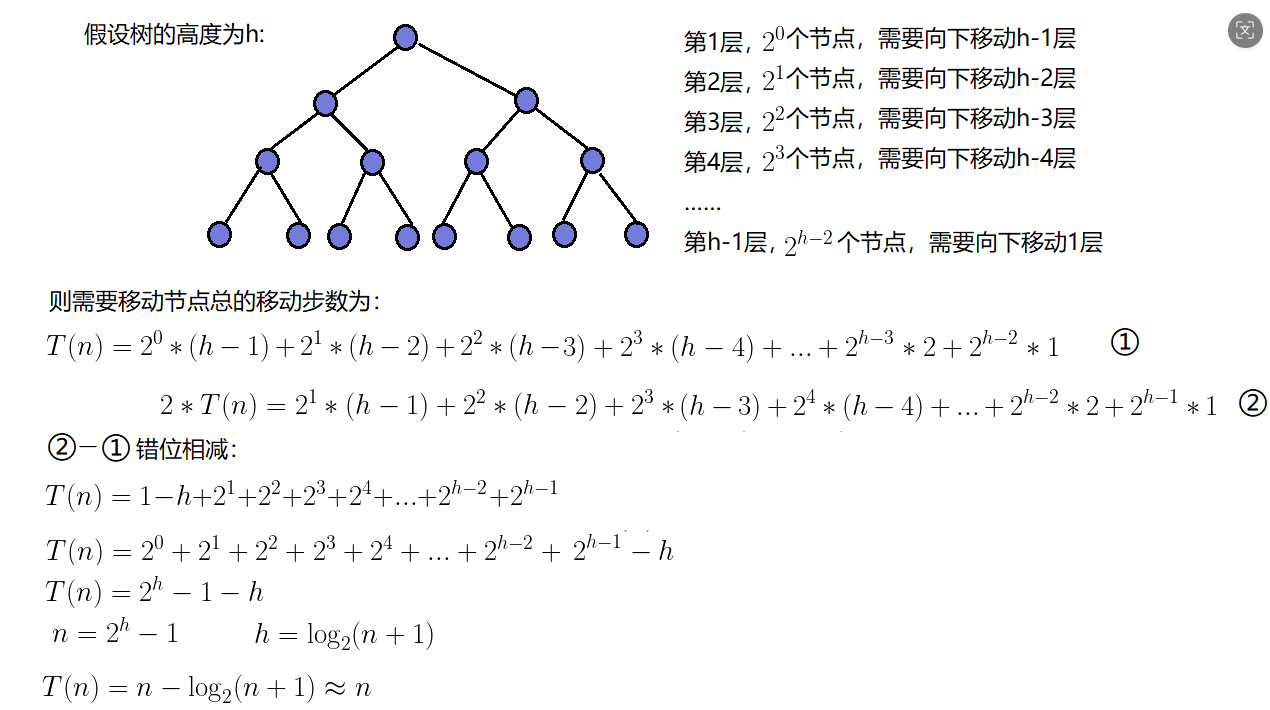
        这张图是分析向下建堆的推导过程，至于这个图我就不和大家分析了，我也有点看不懂，如果你也看不懂，可以看一下我的大白话解析，当然我相信大家肯定都能看懂上面的拉！

        首先向下建堆它的优势是不需要对最底层（叶子节点）进行调整，而二叉树的最后一层节点就差不多是总结的的一半，因此向下建堆就减少了一半的工作量，而这减少一半的工作量就是从O(nlogn)降到O(n)，好了我实在编不下去了，不过理倒是这个理，大家如果想知道为什么去看看别人吧，我实在是做不到！

三.堆的应用

        我们讲了堆，那么它到底有什么作用呢？

        关于它最大的作用其实是讲解TOP-K问题，那什么是TOP-K问题呢？

        TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

        比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

        堆解决的基本思路： 

        1. 用数据集合中前K个元素来建堆：

        前k个最大的元素，则建小堆

        前k个最小的元素，则建大堆

        2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

        将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

        举个例子：假设我们有1000个元素，需要找出其中最大的前10个。首先构建一个包含10个元素的小顶堆，此时堆顶是这10个元素中最小的。剩下的990个元素依次与堆顶比较：如果比堆顶大，就替换堆顶元素并重新调整堆结构，使堆顶保持最小。这样不断筛选，最终堆中的10个元素就是最大的前10个。

四.二叉树链式结构的实现

        4.1 二叉链

class BinaryTreeNode
{
public:
    int _data;
    BinaryTreeNode* _left;//左节点
    BinaryTreeNode* _right;//右节点
};

        二叉链的核心就是left和right，其分别代表着：左节点和右节点！

        4.2 二叉树的遍历

        学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

        按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

        1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

        2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中。

        3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

        

        这三种遍历我们通常均采用递归的方式完成。

#include<iostream>
// 二叉树前序遍历
void PreOrder(Node* root)
{
	if (root == nullptr)
	{
		return;
	}
	std::cout << root->_data << std::endl;
	PreOrder(root->_left);
	PreOrder(root->_right);
}
// 二叉树中序遍历
void InOrder(Node* root)
{
	if (root == nullptr)
	{
		return;
	}
	InOrder(root->_left);
	std::cout << root->_data << std::endl;
	InOrder(root->_right);
}
// 二叉树后序遍历
void PostOrder(Node* root)
{
	if (root == nullptr)
	{
		return;
	}
	PostOrder(root->_left);
	PostOrder(root->_right);
	std::cout << root->_data << std::endl;
}

        下面我通过一张图片带着大家来了解一下前序遍历，然后大家根据这个再去了解中序和后继！

     

                

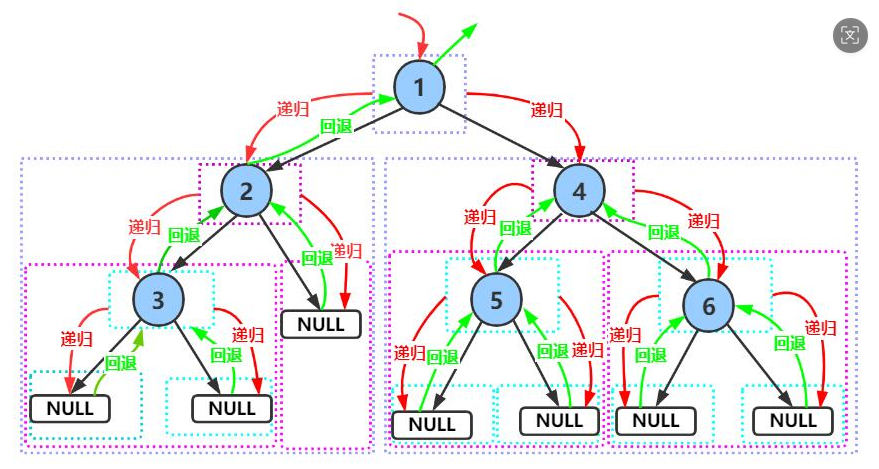
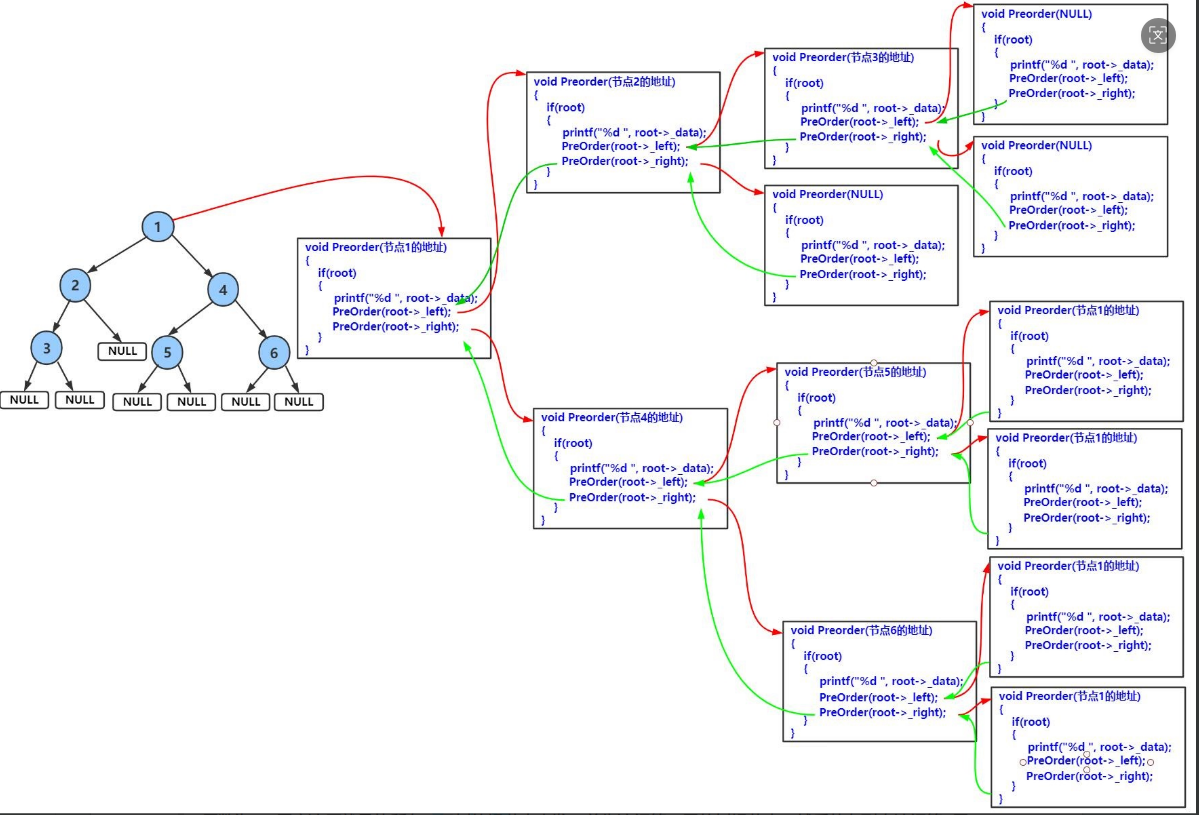
        前序遍历结果：1 2 3 4 5 6

        中序遍历结果：3 2 1 5 4 6

        后序遍历结果：3 2 5 6 4 1

        4.3 层序遍历

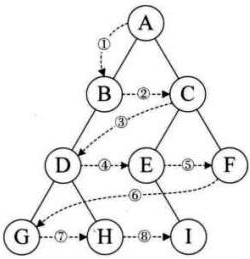
        层序遍历：除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

#include<iostream>
#include<queue>
#include<assert.h>
// 层序遍历
void LevelOrder(Node* root)
{
	assert(root != nullptr);//树不为空
	std::queue<Node*>q;//创建一个栈
	q.push(root);//放入根节点

	while (!q.empty())
	{
		Node* node = q.front();//获取队列首元素
		q.pop();//删除元素

		if (node != nullptr)//该节点不为空，才能保证有左右节点外加数据
		{
			//左节点不为空才放入
			if (node->_left != nullptr)
				q.push(node->_left);//放入左节点

			//右节点不为空才放入
			if (node->_right != nullptr)
				q.push(node->_right);//放入右节点

			std::cout << node->_data << std::endl;//打印节点
		}
	}
}

        关于层序遍历还是需要和大家好好分析一下的！

        首先层序遍历和之前提到的前中后遍历是不同阵营的，层序遍历的实现是更适合迭代，而前中后遍历更适合的是递归，因此这是二者的最大区别！

        首先我们要保证先打印A——B——C，你想到了什么这不就是排队吗，那么排队我们用什么数据结构，大家肯定能想到队列，因此我们就创建一个队列，然后A生B和C，B生D和E，C再生F和G……明白这个我们就大概知道层序遍历的要点了，下面大家就可以根据我上面的代码来实现层序遍历了！

        4.4 选择题

1.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。
该完全二叉树的前序序列为（ ）

A ABDHECFG
B ABCDEFGH
C HDBEAFCG
D HDEBFGCA
2.二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：
HFIEJKG.则二叉树根结点为（）

A E
B F
C G
D H
3.设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，
则二叉树前序遍历序列为____。

A adbce
B decab
C debac
D abcde
4.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，
则按层次输出（同一层从左到右）的序列为（）

A FEDCBA 
B CBAFED
C DEFCBA
D ABCDEF





1.A
2.A
3.D
4.A

        1：如果我们知道层序遍历，我们完全就可以把它画下来因此，此题没啥问题

        2，3：这两题我们直接一起解决了，他们本质都是同一类题目，首先这类题这么做，首先它会给你两中遍历（其中必须有中序遍历）让你求第三个，为什么一定要知道中序，因为前序和后续我们只能知道根节点是那个，只有中序我们才知道左子树有那些，右子树有那些！

        4：你用2，3的方法你同样可以解决，你会惊奇的发现这棵树就是一个丿（即该数的节点只可能有左孩子）
        
        好了，今天的内容就到这里吧，很高兴能和大家分享这么多，如有不足多多包含，感谢大家了！