Machine Learning第三讲[Logistic回归] --（二）Logistic回归模型

内容来自Andrew老师课程Machine Learning的第三章内容的Logistic Regression Model部分。

一、Cost Function（代价函数）

有m个样本的训练集： { ( x ( 1 ) , y ( 1 ) ) , ( x ( 2 ) , y ( 2 ) ) , . . . . , ( x ( m ) , y ( m ) ) } \{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ...., (x^{(m)}, y^{(m)})\} {(x(1),y(1)),(x(2),y(2)),....,(x(m),y(m))}, $X=\left[\begin{array}{c}{x}_0\\ x_1\\ .\\ .\\ .\\ x_n\end{array}\right]\in R^{n+1}$, x 0 = 1 , y ∈ { 0 , 1 } x_0=1, y \in \{0,1\} x0​=1,y∈{0,1}.
在上篇博文中提到假设函数$h_{\theta }(x)：h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$。
那么，我们如何选择参数theta呢？

在线性回归模型中，$J(\theta )=\frac{1}{m}{\sum }_{i=1}^m\frac{1}{2}(h_{\theta }(x^{(i)}-y^{(i)}{)}^2$，令$\frac{1}{2}(h_{\theta }(x^{(i)}-y^{(i)}{)}^2=cost(h_{\theta }(x^{(i)}),y^{(i)})$，为方便记录，将此等式记为：$cost(h_{\theta }(x),y)=\frac{1}{2}(h_{\theta }(x)-y{)}^2$，

因为$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$是非线性的，故$cost(h_{\theta }(x),y)$也是非线性的，将其代入J(theta)，则J(theta)曲线图很有可能出现下列情况，如下左图：

    

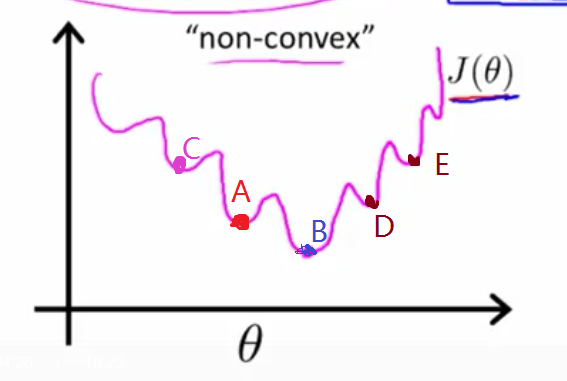
$J(\theta )$ 在这种情况下，不收敛。
即：J存在多个局部最小值（A，B，C，D，E等都是）。但是使用梯度下降法不一定能找到最优值，比如在梯度下降算法走到A点，再往下走发现B点的J值比A点的J值大了，因此算法停止搜索并断定A是最小值点，此时便没有找到最小值。

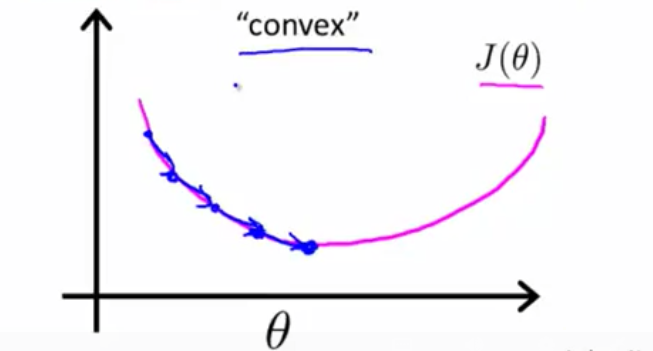
而我们希望出现的右图所示的情况，梯度下降算法能一步一步往下走，直到找到最小值。

产生这种情况的原因是因为$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$中含有平方，故使用线性回归的代价函数来用于logsitic模型是不合适的，因此我们用一个新函数来定义logistic的cost函数：

$$Cost(h_{\theta }(x),y)=\{\begin{array}{cc}-log(h_{\theta }(x))& y=1\\ -log(1-h_{\theta }(x))& y=0\end{array}$$
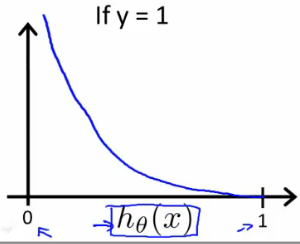
（1）当y=1时，Cost函数图如下所示：

由图可知：
当$h_{\theta }(x)=1$时，$cost=0$；
当$h_{\theta }(x)\to 0$时，$cost\to \infty$。
当y=1，
若预测值$h_{\theta }(x)=1$，则预测值和实际值相同，因此cost=0；
若预测值$h_{\theta }(x)\to 1$，即$h_{\theta }(x)=p(y=1|x;\theta )\to 0$，即预测值为0，因为实际值为1，故代价函数cost为无穷大。

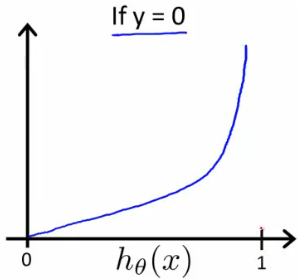
（2）当$y=0$时，Cost函数图如下所示：

由图可知：
当$h_{\theta }(x)=1$，即预测值为1时，而真实值为0，此时cost->∞；
当$h_{\theta }(x)=0$，即预测值为0，而真实值也为0，此时cost=0。

附上一个例题：

二、Simplified Cost Function and Gradient Descent（简化代价函数和梯度下降）

logsitic回归代价函数为：

$$\begin{gathered} J(\theta )=\frac{1}{m}\sum _{i=1}^{m}Cost(h_{\theta }(x^{(i)}),y^{(i)}) \\ Cost(h_{\theta }(x),y)=\{\begin{array}{cc}-log(h_{\theta }(x))& y=1\\ -log(1-h_{\theta }(x))& y=0\end{array} \end{gathered}$$

    Note: $y=0$ or $y=1$ always

我们将这个Cost分段函数写成一个函数，则：

$$Cost(h_{\theta }(x),y)=-ylog(h_{\theta }(x))+[-(1-y)log(1-h_{\theta }(x))]$$

验证一下为什么可以写成这一个式子：
因为y只可能取0或者1：
（1）若$y=1$，代入上式，则$Cost(h_{\theta }(x),y)=-log{h}_{\theta }(x)$满足分段函数表达式。
（2）若$y=0$，代入上式，则$Cost(h_{\theta }(x),y)=-log(1-h_{\theta }(x))$也满足分段函数表达式。
因此这个式子和分段函数表达式是等价式。

（一）J函数

将上述cost函数代入$J(\theta )$，则

$$\begin{array}{rl}J(\theta )& =\frac{1}{m}\sum _{i=1}^{m}cost(h_{\theta }(x^{(i)}),y^{(i)})\\ & =-\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}log{h}_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]\end{array}$$
将$J(\theta )$函数向量化表示为：

$$\begin{array}{rl}h& =g(X\theta )\\ J(\theta )& =\frac{1}{m}(-y^{T}log(h)-(1-y{)}^{T}log(1-h)\end{array}$$

为了求出$\theta$值，我们通过求$minJ(\theta )$来求，即利用梯度下降算法来求。
预测输出是指：输入x值，输出$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$，即$P(y=1|x;\theta )$。

（二）梯度下降算法：

梯度下降公式：

$$\begin{array}{rl}{\theta }_j& ={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )\end{array}$$
（注意同步更新）

将偏导数部分代入得：

$$\begin{array}{rl}{\theta }_j& ={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}\end{array}$$

将梯度下降算法向量表示得：

$$\begin{array}{rl}\theta & =\theta -\frac{\alpha }{m}{X}^T(g(X\theta )-y)\end{array}$$
Note：虽然分类回归的梯度下降函数和线性回归的梯度下降函数看起来一样，但是其并不相同，因为在线性回归中$h_{\theta }(x)={\theta }^{T}x$，而在分类回归中$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$，所以h(x)函数部分不同，导致二者不相同。

三、Advanced Optimization（优化问题）

（1）首先看梯度下降算法，在实现梯度下降算法的过程中，我们需要实现J函数及其偏导数对应的代码：

（2）再来看看除了梯度下降算法之外的其他的优化算法，后三种优化算法性能比较好，但是实现过程比较复杂，理解也比较难（本节不讲述细节）：

（3）举例说明如何实现优化算法的调用，代码细节如下图，其中fminunc()用于实现最小代价函数的调用：

（4）如何将这些优化算法应用到logistic回归中呢？如下图，在具体实现时我们只需要填写相应的实现代码：

我们要做的就是不断探索，将高级优化应用于logistic回归和线性回归以提高寻找最小代价函数对应theta值得效率。

四、逻辑回归算法的并行化

如上所示，逻辑回归的偏导数形式为$\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$，假设数据集共有$K$类，则：

$$\begin{array}{rl}& \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}\\ & =\frac{1}{m}\sum _{k=1}^K\sum _{i\in C_k}(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}\end{array}$$

其中，$C_k$是所有类别的一个partition。所以对于logistic回归来讲，并行的地方是每个类别之间的并行化。

参考文章：[链接](http://blog.csdn.net/u012328159/article/details/51077330 "链接")