1 SVM
1.1 代价函数
在推导svm的代价函数之前,先回顾以下逻辑回归中每一个训练样本的代价函数:
−
(
y
log
h
θ
(
x
)
+
(
1
−
y
)
log
(
1
−
h
θ
(
x
)
)
)
- \left( y \log h _ { \theta } ( x ) + ( 1 - y ) \log \left( 1 - h _ { \theta } ( x ) \right) \right)
−(yloghθ(x)+(1−y)log(1−hθ(x)))
=
−
y
log
1
1
+
e
−
θ
T
x
−
(
1
−
y
)
log
(
1
−
1
1
+
e
−
θ
T
x
)
= - y \log \frac { 1 } { 1 + e ^ { - \theta ^ { T } x } } - ( 1 - y ) \log \left( 1 - \frac { 1 } { 1 + e ^ { - \theta ^ { T } x } } \right)
=−ylog1+e−θTx1−(1−y)log(1−1+e−θTx1)
当y=1时,上面的函数就为
−
log
1
1
+
e
−
z
- \log \frac { 1 } { 1 + e ^ { - z } }
−log1+e−z1,图像就如下图左,该函数的自变量为z,我们取z=1点,然后画出如下图所示的粉丝线,就时支持向量机的
C
o
s
t
1
(
z
)
Cost_1(z)
Cost1(z);当y=0时,上面的函数为
−
log
(
1
−
1
1
+
e
−
z
)
- \log \left( 1 - \frac { 1 } { 1 + e ^ { - z } } \right)
−log(1−1+e−z1),图像就如下图右,同理我们画出支持向量机的
C
o
s
t
0
(
z
)
Cost_0(z)
Cost0(z)。
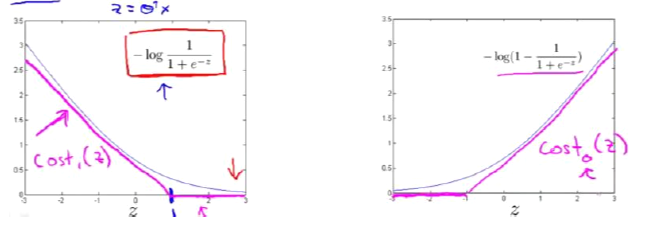
在画出支持向量机的两个costterm后,我们就可以构建出支持向量机,第一行为逻辑回归的代价函数,在进行替换后,我们就得到了支持向量机的代价函数:
min
θ
1
m
[
∑
i
=
1
m
y
(
i
)
(
−
log
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
(
−
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
)
]
+
λ
2
m
∑
j
=
1
n
θ
j
2
\min_\theta \frac{1}{m}\left[\sum _ { i = 1 } ^ { m } y ^ { ( i ) } \left( - \log h _ { \theta } \left( x ^ { ( i ) } \right) \right)+ \left( 1 - y ^ { ( i ) } \right)\left(-log\left(1-h_\theta\left(x^{(i)}\right)\right)\right)\right]+ \frac { \lambda } { 2 m } \sum _ { j = 1 } ^ { n } \theta _ { j } ^ { 2 }
θminm1[i=1∑my(i)(−loghθ(x(i)))+(1−y(i))(−log(1−hθ(x(i))))]+2mλj=1∑nθj2
min
θ
C
∑
i
=
1
m
[
y
(
i
)
cost
1
(
θ
T
x
(
i
)
)
+
(
1
−
y
(
i
)
)
cost
0
(
θ
T
x
(
i
)
)
]
+
1
2
∑
i
=
1
n
θ
j
2
\min _ { \theta } C \sum _ { i = 1 } ^ { m } \left[ y ^ { ( i ) } \operatorname { cost } _ { 1 } \left( \theta ^ { T } x ^ { ( i ) } \right) + \left( 1 - y ^ { ( i ) } \right) \operatorname { cost } _ { 0 } \left( \theta ^ { T } x ^ { ( i ) } \right) \right] + \frac { 1 } { 2 } \sum _ { i = 1 } ^ { n } \theta _ { j } ^ { 2 }
θminCi=1∑m[y(i)cost1(θTx(i))+(1−y(i))cost0(θTx(i))]+21i=1∑nθj2
在支持向量机的代价函数中,要注意以下两点:
- 我们删去了1/m,由于1/m对于求解代价函数的最优值并没有实质性影响
- 我们在第一项中加上了C,在正则化项中去掉了
λ
\lambda
λ,但是他们的作用是相同的,可以理解为
C
=
1
/
λ
C=1/\lambda
C=1/λ。当C大,则
λ
\lambda
λ小,会导致过拟合,高方差;当C小,则
λ
\lambda
λ大,会导致低拟合,高偏差。
另外,与逻辑回归输出概率不同的是,支持向量机使用参数 θ \theta θ来直接预测y=1还是=0
1.2 大边界
在SVM中如果 y = 1 y=1 y=1,那么我们希望 θ T x ≥ 1 \theta^Tx \ge 1 θTx≥1;如果 y = 0 y=0 y=0,那么我们希望 θ T x ≤ − 1 \theta^Tx \le -1 θTx≤−1,这样才能最小化SVM代价函数的第一项,如下图所示。

在遵从上述约束的情况下,使用SVM计算决策边界,将会得到下图中的黑色边界,而不是其他颜色的边界,其中黑色边界与蓝色边界之间的的距离称为间距,而SVM要做的就是努力用一个最大的间距来分离样本,所以SVM也被称为大间距分类器,这个边界就是对代价函数进行优化的结果。下面为大间距分类器的数学原理。
假设这里的特征数为n=2,这样我们有两个特征 x 1 , x 2 x_1,x_2 x1,x2,对应的参数向量为 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2,在二维坐标系中可以表示如下图。其中 p ( i ) p^{(i)} p(i)为向量x在向量 θ \theta θ上的投影,那么 θ T x = p ( i ) ∣ ∣ θ ∣ ∣ = θ 1 x 1 ( i ) \theta^Tx=p^{(i)}||\theta||=\theta_1x_1^{(i)} θTx=p(i)∣∣θ∣∣=θ1x1(i)。因此,如果 y = 1 y=1 y=1,那么 p ( i ) ∣ ∣ θ ∣ ∣ ≥ 1 p^{(i)}||\theta|| \ge 1 p(i)∣∣θ∣∣≥1;如果 y = 0 y=0 y=0,那么 p ( i ) ∣ ∣ θ ∣ ∣ ≤ − 1 p^{(i)}||\theta|| \le -1 p(i)∣∣θ∣∣≤−1。
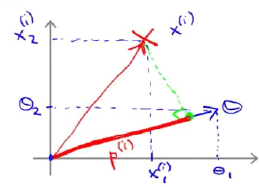
现在我们有下面的训练样本,很明显最优的分界线应该是y轴。当我们取下左图中绿线为分界线时,对应的向量 θ \theta θ为与边界线正交的蓝线。因为 y ( 1 ) = 1 y^{(1)}=1 y(1)=1,那么 p ( 1 ) ∣ ∣ θ ∣ ∣ ≥ 1 p^{(1)}||\theta|| \ge 1 p(1)∣∣θ∣∣≥1,但是 p ( 1 ) p^{(1)} p(1)在这里非常小,那就意味着需要 θ \theta θ的范数非常大,但是由于正则化项的限制, θ \theta θ不能过大。同理 p ( 2 ) ∣ ∣ θ ∣ ∣ ≤ − 1 p^{(2)}||\theta|| \le -1 p(2)∣∣θ∣∣≤−1,同样需要 θ \theta θ的范数非常大,所以这个参数向量 θ \theta θ的结果并不好。
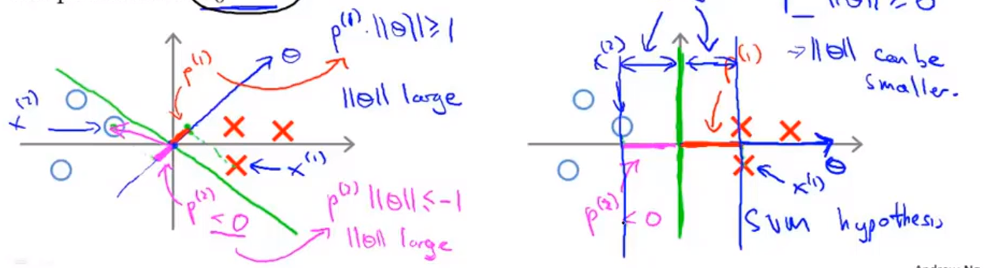
当我们选择y轴作为边界时,如上右图所示,此时对应的向量 θ \theta θ为x轴,样本在 θ \theta θ上的投影的长度会变大,这样的话 θ \theta θ的范数会变小一些,因此支持向量机会选择右边的决策边界。这里的 p ( 1 ) p ( 2 ) p^{(1)}p^{(2)} p(1)p(2)就是指样本到 θ \theta θ向量的距离,通过让间距变大,支持向量机最终会找到一个较小的 θ \theta θ,这是支持向量机最小化目标函数的目的,也因此支持向量机被称作最大间距分类器。
2 核函数
之前我们讨论过使用高级数的多项式模型可以解决非直线的分割问题,我们采用
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
1
x
2
+
θ
4
x
1
2
+
θ
5
x
2
2
+
…
\theta _ { 0 } + \theta _ { 1 } x _ { 1 } + \theta _ { 2 } x _ { 2 } + \theta _ { 3 } x _ { 1 } x _ { 2 } + \theta _ { 4 } x _ { 1 } ^ { 2 } + \theta _ { 5 } x _ { 2 } ^ { 2 } + \dots
θ0+θ1x1+θ2x2+θ3x1x2+θ4x12+θ5x22+…的模型来实现上述的划分,其中
f
1
=
x
1
,
f
2
=
x
2
,
f
3
=
x
1
x
2
,
f
4
=
x
1
2
,
f
5
=
x
2
2
f _ { 1 } = x _ { 1 } , f _ { 2 } = x _ { 2 } , f _ { 3 } = x _ { 1 } x _ { 2 } , f _ { 4 } = x _ { 1 } ^ { 2 } , f _ { 5 } = x _ { 2 } ^ { 2 }
f1=x1,f2=x2,f3=x1x2,f4=x12,f5=x22,那么除此之外,利用和函数来计算出新的特征,可以构造更好的新特征。
对于给定的某个训练集实例,可以利用x的各个特征
x
j
x_j
xj与我们预先选定的地标(landmarks)
l
(
1
)
,
l
(
2
)
,
l
(
3
)
l^{(1)},l^{(2)},l^{(3)}
l(1),l(2),l(3)的近似程度来选取新的特征
f
1
,
f
2
,
f
3
f_1,f_2,f_3
f1,f2,f3。其中
f
1
=
similarity
(
x
,
l
(
1
)
)
=
exp
(
−
∥
x
−
l
(
1
)
∥
2
2
σ
2
)
∥
x
−
l
(
1
)
∥
2
=
∑
j
=
1
n
(
x
j
−
l
j
(
1
)
)
2
f _ { 1 } = \text { similarity } \left( x , l ^ { ( 1 ) } \right) = \exp \left( - \frac { \left\| x - l ^ { ( 1 ) } \right\| ^ { 2 } } { 2 \sigma ^ { 2 } } \right)\qquad\left\| x - l ^ { ( 1 ) } \right\| ^ { 2 } = \sum _ { j = 1 } ^ { n } \left( x _ { j } - l _ { j } ^ { ( 1 ) } \right) ^ { 2 }
f1= similarity (x,l(1))=exp(−2σ2∥∥x−l(1)∥∥2)∥∥∥x−l(1)∥∥∥2=j=1∑n(xj−lj(1))2在上面的公式中
similarity
(
x
,
l
(
1
)
)
\text { similarity } \left( x , l ^ { ( 1 ) } \right)
similarity (x,l(1))就是核函数,具体来说是一个高斯核函数(Gaussian Kernel)。
当一个训练实例x与地标l之间很近,那么
f
1
=
exp
(
−
∥
x
−
l
(
1
)
∥
2
2
σ
2
)
≈
exp
(
−
0
2
σ
2
)
≈
1
f _ { 1 } = \exp \left( - \frac { \left\| x - l ^ { ( 1 ) } \right\| ^ { 2 } } { 2 \sigma ^ { 2 } } \right)\approx\exp \left( - \frac {0 } { 2 \sigma ^ { 2 } } \right)\approx1
f1=exp(−2σ2∥x−l(1)∥2)≈exp(−2σ20)≈1;如果两者较远
f
1
≈
0
f _ { 1 } \approx0
f1≈0。
在下图中的例子中,红色的实例离
l
(
1
)
l^{(1)}
l(1)很近,但是离
l
(
2
)
,
l
(
3
)
l^{(2)},l^{(3)}
l(2),l(3)较远所以
f
1
=
1
,
f
2
,
f
3
=
0
f_1=1,f_2,f_3=0
f1=1,f2,f3=0;同理对于绿色点来说
f
2
=
1
,
f
1
,
f
3
=
0
f_2=1,f_1,f_3=0
f2=1,f1,f3=0;蓝色点
f
3
=
1
,
f
1
,
f
2
=
0
f_3=1,f_1,f_2=0
f3=1,f1,f2=0。那么通过使用生成的新特征进行训练,便可以得到右边的
θ
\theta
θ值,红色边界即为svm预测的分类边界。
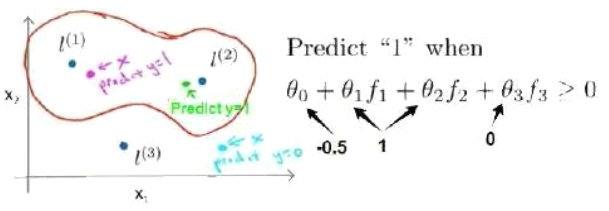
在选择地标L时,通常是根据训练集的数量选择地标的数量,即
l
(
1
)
=
x
(
1
)
,
l
(
2
)
=
x
(
2
)
,
…
,
l
(
m
)
=
x
(
m
)
l^ { ( 1 ) } = x ^ { ( 1 ) } ,l ^ { ( 2 ) } = x ^ { ( 2 ) } , \ldots ,l ^ { ( m ) } = x ^ { ( m ) }
l(1)=x(1),l(2)=x(2),…,l(m)=x(m),这样做的好处是:我们得到的新特征是建立在原有特征与训练集中所有其他特征之间距离的基础之上的。那么根据地标计算新特征,对于一个训练实例
(
x
(
i
)
,
y
(
i
)
)
\left( x ^ { ( i ) } , y ^ { ( i ) } \right)
(x(i),y(i)),构建一个新的实例
(
f
(
i
)
,
y
(
i
)
)
\left( f ^ { ( i ) } , y ^ { ( i ) } \right)
(f(i),y(i)):
f
(
i
)
=
[
f
0
(
i
)
=
1
f
1
(
i
)
=
s
i
m
(
x
(
i
)
,
l
(
1
)
)
f
2
(
i
)
=
s
i
m
(
x
(
i
)
,
l
(
2
)
)
f
i
(
i
)
=
s
i
m
(
x
(
i
)
,
l
(
i
)
)
=
e
0
=
1
f
m
(
i
)
=
s
i
m
(
x
(
i
)
,
l
(
m
)
)
]
f ^ { ( i ) } = \left[ \begin{array} { c } { f _ { 0 } ^ { ( i ) } = 1 } \\ { f _ { 1 } ^ { ( i ) } = sim \left( x ^ { ( i ) } , l ^ { ( 1 ) } \right) } \\ { f _ { 2 } ^ { ( i ) } = sim \left( x ^ { ( i ) } , l ^ { ( 2 ) } \right) } \\ { f _ { i } ^ { ( i ) } = sim \left( x ^ { ( i ) } , l ^ { ( i ) } \right) = e ^ { 0 } = 1 } \\ { f _ { m } ^ { ( i ) } = \operatorname sim \left( x ^ { ( i ) } , l ^ { ( m ) } \right) } \end{array} \right]
f(i)=⎣⎢⎢⎢⎢⎢⎡f0(i)=1f1(i)=sim(x(i),l(1))f2(i)=sim(x(i),l(2))fi(i)=sim(x(i),l(i))=e0=1fm(i)=sim(x(i),l(m))⎦⎥⎥⎥⎥⎥⎤
在求得新特征后,支持向量机的代价函数就可以变为
min
C
∑
i
=
1
m
[
y
(
i
)
cost
1
(
θ
T
f
(
i
)
)
+
(
1
−
y
(
i
)
)
cost
0
(
θ
T
f
(
i
)
)
]
+
1
2
∑
j
=
1
n
=
m
θ
j
2
\min C \sum _ { i = 1 } ^ { m } \left[ y ^ { ( i ) } \operatorname { cost } _ { 1 } \left( \theta ^ { T } f ^ { ( i ) } \right) + \left( 1 - y ^ { ( i ) } \right) \operatorname { cost } _ { 0 } \left( \theta ^ { T } f ^ { ( i ) } \right) \right] + \frac { 1 } { 2 } \sum _ { j = 1 } ^ { n = m } \theta _ { j } ^ { 2 }
minCi=1∑m[y(i)cost1(θTf(i))+(1−y(i))cost0(θTf(i))]+21j=1∑n=mθj2
另外,支持向量机也可以不使用核函数,这时也称其为线性核函数(linear kernel)。当我们的训练集特征非常多但实例非常少的时候,就应该使用不带核函数的支持向量机。
在支持向量机中参数C和
σ
\sigma
σ影响如下:
- C 较大时,相当于λ 较小,可能会导致过拟合,高方差;
- C 较小时,相当于λ 较大,可能会导致低拟合,高偏差;
- σ \sigma σ 较大时,可能会导致低方差,高偏差,低拟合;
- σ \sigma σ 较小时,可能会导致低偏差,高方差,过拟合。
3 使用支持向量机
在向量机的核函数方面,除了高斯核函数之外,还有其他一些选择:
- 多项式核函数(Polynomial Kernel)
- 字符串核函数(String kernel)
- 卡方核函数(chi-square kernel)
- 直方图交集核函数(histogram intersection kernel)
在使用向量机时,要选择如下参数:
- 参数C 的选择
- 选择核函数参数或你想要使用的核函数
关于逻辑回归和svm的选择:
- 如果n要比m大得多,选用逻辑回归模型或者不带核函数的支持向量机
- 如果n 较小,而且m 大小中等,例如n 在1-1000 之间,而m在10-10000 之间,使用高斯核函数的支持向量机
- 如果n 较小,而m 较大,例如n 在1-1000之间,而m 大于50000,则使用支持向量机会非常慢,解决方案是创造、增加更多的特征,然后使用逻辑回归或不带核函数的支持向量机。
另外神经网络对以上条件都会有很好的表现,但是神经网络可能会非常慢,选择支持向量机的原因主要在于它的代价函数是凸函数,不存在局部最小值。





















 386
386











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








