Pku1200 Crazy Search（Rabin Karp）

题意：先给两个整数n和nc，然后给出一个字符串，问有多少种不同的长度为n的子串，nc为字符串中不同的字符数。

思路：数据范围比较大，用哈希的方式可以解决。采用Rabin karp字符串匹配设计哈希函数即可。

以下有关Rabin karp的讲解转载自： http://blog.csdn.net/touzani/article/details/1632149

字符串匹配(String matching)

问题的形式定义: 假设文本（Text）是一个长度为n的数组T[1…n], 模式(Pattern)是一个长度为 m ≤  n.的数组P[1..m];. 又假设P和T中的元素都属于有限字母表Σ 中的字符。 P和T常称为字符串。

如果0 ≤ s ≤ n – m 且T[s+1..s+m]=P[1…m], 则说P在T中出现且位移为s，此时成s为一个有效位移。

字符串匹配问题就变成在一个在一段制定的文本T中找出模式P的所有有效位移的问题。

 

下图给出了将要介绍的字符串匹配算法以及它们的预处理时间和匹配时间。

算法	预处理时间	匹配时间
朴素算法	0	O(( n -  m + 1) m)
Rabin-Karp	Θ( m)	O(( n -  m + 1) m)
有限自动机算法	O( m |Σ|)	Θ( n)
KMP算法	Θ( m)	Θ( n)

 

记号：

用Σ* 表示用字母表Σ中的所有有限长度的字符串的集合

字符串x的长度用| x |表示。

wy表示两个字符串w和y的连接。| wy | = | x |+| y |

 

 

字符串前缀  后缀

如果某个字符串 y ∈ Σ*，使得x＝wy 。则称w是x的前缀, 记为w � x 。 如果w是x的后缀，记为w � x

 

可以把字符串匹配问题描述为 找出0 ≤ s ≤ n-m 并满足P � T_s+m的所有位移s

 

1.)朴素的字符串匹配算法

NAIVE-STRING-MATCHER(T, P)

1 n ← length[T]

2 m ← length[P]

3 for s ← 0 to n - m
4     do if P[1 ‥ m] = T[s + 1 ‥ s + m]         // 隐含着一个循环
5           then print "Pattern occurs with shift" s

时间复杂度为 O(( n -  m + 1) m), 如果 m = � n/2�. 那么时间复杂度为Θ( n ²), 这个算法效率不高，原因在于对于s的一个值，获得的关于文本的信息在考虑s的其他值时完全被忽略了。

例如，如果 P＝aaab，设s＝0 是有效的，那么 s＝1， 2， 3 就不可能是有效位移，因为T[4]=b.

 

 

2.) Rabin-Karp字符串匹配算法,

 

实际应用中，Rabin和Karp建议的字符串匹配算法能较好地运行，还可以归纳出有关问题地其他算法，如二维模式匹配。

 

假定字符集Σ ＝{0, 1, 2, ……， 9}， 每一个字符对应一个十进制数字

（一般情况, 假定每个字符是基数为d的表示法中的一个数字， d=|Σ|。)可以用一个长度为k的十进制数字来表示由k个连续字符组成的字符串.

因此，字符串"31415" 对应于十进制数31415

已知模式P[1..m]，设p表示其相应十进制数地值，类似地， 对于给定的文本T[1..n]. 用

t_s 表示长度为m的子字符串  T[ s + 1 ‥  s +  m]（  s = 0, 1, . . . ,  n –  m），  t_s =  p 当且仅当 [ s + 1 ‥  s +  m] =  P[1 ‥ m]; 因此s是有效位移当且仅当  t_s =  p. (暂不考虑p和 t_s 可能是很大的数的情况)。

可以用霍纳规则(Horner’s rule) 在Θ(m) 的时间内计算p的值

p = P[m] + 10 (P[m - 1] + 10(P[m - 2] + · · · + 10(P[2] + 10P[1]) )).

 

Horner’s rule

类似地，可以在Θ( m)时间内，根据T[1..m]计算出 t ₀ 的值。

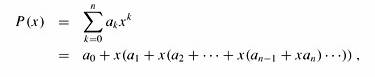
如果能在总共Θ(n - m + 1) 时间内计算出所有的t_s 的值，那么通过把p值与每个t_s（有n－m＋1个）进行比较，就能够在Θ(m) + Θ(n - m + 1)= Θ(n) 时间内求出所有有效位移。（计算出1个t_s 就跟p比较，处理结果。）

为了在Θ(n - m) 时间内计算出剩余的值t₁, t₂, . . . , t_n-m 可以在常数的时间内根据t_s计算出t_s+1，先看例子，假如m = 5，t_s = 31415, 我们去掉高位数字T [s + 1] = 3，然后在加入一个低位数字T [s + 5 + 1]（假设为2)，得到：

t_s+1 = 10(31415 - 10000 • 3) + 2 = 14152.

总结出公式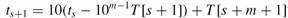：      ——公式1

如果预先计算出10 ^{m -1}（通过数论中的技术可以在 O(lg  m)完成, 在这里只需简单地在 O( m）时间内计算出就可以)。那么就可以在常数时间计算出 t_{s +1}

因此，可以在Θ(m)时间内计算出p和t_0。然后在Θ(n - m + 1)时间内计算出t₁, . . . , t_n-m 并完成匹配。

现在来解决唯一的问题，就是计算中p和t_s的值可能太大，超出计算机字长，不能方便地进行处理。如果p包含m个字符，那么， 关于在p上地每次算术运算需要“常数”时间这一假设就不合理了，幸运的是，对这一问题存在一个简单的补救方法，对一个合适的模q来计算p和t_s的模，每个字符是一个十进制数，因为p和t₀ 以及公式1计算过程都可以对模q进行，所以可以在Θ(m)时间内计算出模q的p值，在Θ(n - m + 1)时间内计算出模q的所有t_s值，通常选模q为一个素数，使得10q正好为一个计算机字长，单精度算术运算就可以执行所有必要的运算过程。 一般情况下，采用d进制的字母表{0, 1, . . . , d - 1}, 所选的q要满足d*q < 字长，调整公式1， 使其为：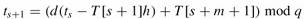

其中的 h =  d ^{m -1} (mod  q)

但是加入模q后，由t_s ≡ p (mod q)不能说明 t_s = p. 但t_s � p (mod q), 可以说明 t_s ≠ p,

因此当 t_s ≡  p (mod  q)时， 再用朴素的字符串匹配算法验证 t_s =  p。. 如果q足够大，可以期望伪命中很少出现。

 

 

算法

RABIN-KARP-MATCHER(T, P, d, q)

 1 n ← length[T]

 2 m ← length[P]

 3 h ← dm-1 mod q

 4 p ← 0

 5 t0 ← 0

 6 for i ← 1 to m           � Preprocessing.

 7     do p ← (dp + P[i]) mod q

 8        t0 ← (dt0 + T[i]) mod q

 9 for s ← 0 to n - m       � Matching.

10     do if p = ts

11           then if P[1 ‥ m] = T [s + 1 ‥ s + m]

12                   then print "Pattern occurs with shift" s

13        if s < n - m

14           then ts+1 ← (d(ts - T[s + 1]h) + T[s + m + 1]) mod q

 

c++代码

void RABIN_KARP_MATCHER(string T, string P, int d, int q)  
/* 
搜索P在T中出现的位置
参数d :字母表的进制，亦即是字母表的元素个数
参数q : 一个较大的素数， 只需d*q < 字长
*/
{
    
    int n= T.length();
    int m= P.length();
    if( n < m)
        return ;
    int i, h=1;
    for(i=1; i<=m-1; i++)   // caculate h 
        h = h*d%q;

    int p=0, t=0;
    for(i=0; i<m; i++)      //  预处理，计算p， t0 
    {
        p = (( d*p + P[i]) % q); 
        t = (( d*t + T[i]) % q);
    }

    int s;
    for(s=0; s < n-m+1; s++)   //    匹配
    {
        if( p == t )
        {
            for(i=0; i<m; i++)        // 进一步验证
                if(P[i]!=T[s+i])
                    break;

            if(i==m)
                cout<<"Pattern ocurs with shift "<<s<<endl;
        }
        if( s < n-m )
            t= (  d* (t - T[s]*h%q + q) + T[s+m])  % q;  // 计算ts+1
    }
    cout<<"string matching ends"<<endl;
    return  ;
}

  关于C++ % 运算符例子，见

http://blog.csdn.net/touzani/archive/2007/05/25/1624883.aspx

用Rabin_Karp 算法解的题目：http://blog.csdn.net/touzani/archive/2007/05/15/1609265.aspx 

RABIN_KARP_MATCHER预处理时间为Θ(m) 匹配时间最坏情况下为Θ((n - m + 1)m)，

因为Rabin_Karp算法跟朴素的字符串匹配算法一样，对每个有效位移进行显示验证，如果P = a^m and T = aⁿ, 则验证所需时间为Θ((n - m + 1)m), 因为n - m + 1个可能的位移中每一个都是有效位移。

实际应用中，有效位移数很少（常数c个），因此期望的匹配时间为O((n - m + 1) + cm) = O(n+m), 选取的素数q比p的长度m大得多。

通常处理ASCII码字符, d＝128, 素数q可选6999997。

附上AC代码：

#include <bits/stdc++.h>
using namespace std;
 
typedef long long ll;
const int INF=0x3f3f3f3f;
const int H=16000000;
const int maxn=4005;
int n,nc;
char s[H];
int flag[maxn];
int Hash[H];
 
int main(){
    scanf("%d%d",&n,&nc);
        scanf("%s",s);
        memset(flag,0,sizeof(flag));
        memset(Hash,0,sizeof(Hash));
        int len=strlen(s),num=1;
        for(int i=0;i<len;i++){
            if(!flag[s[i]]){
                flag[s[i]]=num++;
            }
        }
        int count=len-n+1;
        for(int i=0;i<len-n+1;i++){
            int sum=0;
            for(int j=i;j<i+n;j++){
                sum=sum*nc+flag[s[j]];
            }
            sum=sum%H;
            if(Hash[sum]) count--;
            else Hash[sum]=1;
        }
        printf("%d\n",count);
    return 0;
}