1 矩阵基础
1.0 理解矩阵
如果对矩阵的概念已经模糊,推荐国内一人写的《理解矩阵by孟岩》系列,其中,抛出了很多有趣的观点,我之前在阅读的过程中做了些笔记,如下:
“1、简而言之:矩阵是线性空间里的变换的描述,相似矩阵则是对同一个线性变换的不同描述。
那,何谓空间?本质而言,“空间是容纳运动的一个对象集合,而变换则规定了对应空间的运动”by孟岩。在线性空间选定基后,向量刻画对象的运动,运动则通过矩阵与向量相乘来施加。然,到底什么是基?坐标系也。
2、有了基,那么在(1)中所言的则应是:矩阵是线性空间里的变换的描述,相似矩阵则是对同一个线性变换在不同基(坐标系)下的不同描述。
出来了两个问题,一者何谓变换,二者不同基(坐标系)如何理解?事实上,所谓变换,即空间里从一个点(元素/对象)到另一个(元素对象)的跃迁,矩阵用来描述线性变换。基呢?通过前面已知,矩阵无非不过就是用来描述线性空间中的线性变换的一个东西而已,线性变换为名词,矩阵为描述它的形容词,正如描述同一个人长得好看可以用多个不同形容词"帅”"靓”描述,同一个线性变换也可以由多个不同的矩阵来描述,而由哪一个矩阵描述它,则由基(坐标系)确定。
3、前面说了基,坐标系也,形象表述则为角度,看一个问题的角度不同,描述问题得到的结论也不同,但结论不代表问题本身,同理,对于一个线性变换,可以选定一组基,得到一个矩阵描述它,换一组基,得到不同矩阵描述它,矩阵只是描述线性变换非线性变换本身,类比给一个人选取不同角度拍照。
4、前面都是说矩阵描述线性变换,然,矩阵不仅可以用来描述线性变换,更可以用来描述基(坐标系/角度),前者好理解,无非是通过变换的矩阵把线性空间中的一个点给变换到另一个点上去,但你说矩阵用来描述基(把一个坐标系变换到另一个坐标系),这可又是何意呢?实际上,变换点与变换坐标系,异曲同工!
(@坎儿井围脖:矩阵还可以用来描述微分和积分变换。关键看基代表什么,用坐标基就是坐标变换。如果基是小波基或傅里叶基,就可以用来描述小波变换或傅里叶变换)
5、矩阵是线性运动(变换)的描述,矩阵与向量相乘则是实施运动(变换)的过程,同一个变换在不同的坐标系下表现为不同的矩阵,但本质/征值相同,运动是相对的,对象的变换等价于坐标系的变换,如点(1,1)变到(2,3),一者可以让坐标点移动,二者可以让X轴单位度量长度变成原来1/2,让Y轴单位度量长度变成原来1/3,前后两者都可以达到目的。
6、Ma=b,坐标点移动则是向量a经过矩阵M所描述的变换,变成了向量b;变坐标系则是有一个向量,它在坐标系M的度量下结果为a,在坐标系I(I为单位矩阵,主对角为1,其它为0)的度量下结果为b,本质上点运动与变换坐标系两者等价。为何?如(5)所述,同一个变换,不同坐标系下表现不同矩阵,但本质相同。
7、Ib,I在(6)中说为单位坐标系,其实就是我们常说的直角坐标系,如Ma=Ib,在M坐标系里是向量a,在I坐标系里是向量b,本质上就是同一个向量,故此谓矩阵乘法计算无异于身份识别。且慢,什么是向量?放在坐标系中度量,后把度量的结果(向量在各个坐标轴上投影值)按顺序排列在一起,即成向量。
8、b在I坐标系中则是Ib,a在M坐标系中则是Ma,故而矩阵乘法MxN,不过是N在M坐标系中度量得到MN,而M本身在I坐标系中度量出。故Ma=Ib,M坐标系中的a转过来在I坐标系中一量,却成了b。如向量(x,y)在单位长度均为1的直角坐标系中一量,是(1,1),而在X轴单位长度为2.Y轴单位长度为3一量则是(2,3)。
9、何谓逆矩阵?
Ma=Ib,之前已明了坐标点变换a-〉b等价于坐标系变换M-〉I,但具体M如何变为I呢,答曰让M乘以M的逆矩阵。以坐标系
为例,X轴单位度量长度变为原来的1/2,Y轴单位度量长度变为原来的1/3,即与矩阵
相乘,便成直角坐标系I。即对坐标系施加变换,即让其与变换矩阵相乘。 ”
1.1 一堆基础概念
根据wikipedia的介绍,在矩阵中,单位矩阵 如下图所示:
单位向量又是什么呢?数学上,赋范向量空间中的单位向量就是长度为 1 的向量。欧几里得空间中,两个单位向量的点积就是它们之间角度的余弦(因为它们的长度都是 1)。
一个非零向量u 的正规化向量(即单位向量)u',就是平行于u的单位向量,记作:
这里分母是u 的范数(长度)。
何谓点积?点积又称内积,两个向量
![]() a = [a1, a2,…, an],
a = [a1, a2,…, an],
![]() b= [b1, b2,…, bn]的点积定义为:
b= [b1, b2,…, bn]的点积定义为:
这里的Σ指示求和符号。
例如,两个三维向量[1, 3, -5]和[4, -2, -1]的点积是:
使用矩阵乘法并把(纵列)向量当作n×1 矩阵,点积还可以写为:
除了上面的代数定义外,点积还有另外一种定义:
几何定义。在欧几里得空间中,点积可以直观地定义:
正交是垂直这一直观概念的推广,若内积空间中两向量的内积(即点积)为0,则称它们是正交的,相当于这两向量垂直,换言之,如果能够定义向量间的夹角,则正交可以直观的理解为垂直。而正交矩阵(orthogonal matrix)是一个元素为实数,而且行与列皆为正交的单位向量的方块矩阵(方块矩阵,或简称方阵,是行数及列数皆相同的矩阵。)
若数字

![]() 和非零向量
和非零向量
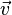
![]() 满足
满足
![]()
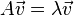 ,则
,则

![]() 为
为
![]()
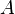 的一个特征向量,
的一个特征向量,
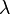
![]() 是其对应的特征值。 换句话说,在
是其对应的特征值。 换句话说,在

![]() 这个方向上,
这个方向上,
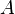
![]() 做的事情无非是把
做的事情无非是把
![]()
 沿其
沿其

![]() 的方向拉长/缩短了一点(而不是毫无规律的多维变换),
的方向拉长/缩短了一点(而不是毫无规律的多维变换),
 则是表示沿着这个方向上拉伸了多少的比例。 简言之,
则是表示沿着这个方向上拉伸了多少的比例。 简言之,
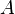 对
对
 做了手脚,使得向量
做了手脚,使得向量
 变长或变短了,但
变长或变短了,但
 本身的方向不变。
本身的方向不变。

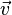
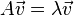 ,则
,则

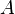 的一个特征向量,
的一个特征向量,
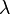

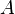
 沿其
沿其

 则是表示沿着这个方向上拉伸了多少的比例。 简言之,
则是表示沿着这个方向上拉伸了多少的比例。 简言之,
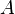 对
对
 做了手脚,使得向量
做了手脚,使得向量
 变长或变短了,但
变长或变短了,但
 本身的方向不变。
本身的方向不变。
矩阵的迹是
![]() 矩阵
矩阵
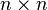 的对角线元素之和,也是其
的对角线元素之和,也是其
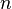
![]() 个特征值之和。
个特征值之和。
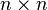 的对角线元素之和,也是其
的对角线元素之和,也是其
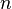
更多矩阵相关的概念可以查阅相关wikipedia,或《矩阵分析与应用》。
2 拉普拉斯矩阵
2.1 Laplacian matrix的定义
拉普拉斯矩阵(Laplacian matrix)),也称为
基尔霍夫矩阵, 是表示图的一种矩阵。给定一个有n个顶点的图
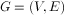 ,其拉普拉斯矩阵被定义为:
,其拉普拉斯矩阵被定义为:
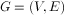 ,其拉普拉斯矩阵被定义为:
,其拉普拉斯矩阵被定义为:
其中
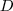 为图的度矩阵,
为图的度矩阵,
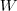 为图的邻接矩阵。
为图的邻接矩阵。
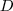 为图的度矩阵,
为图的度矩阵,
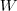 为图的邻接矩阵。
为图的邻接矩阵。
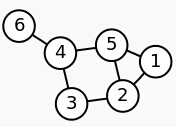
举个例子。给定一个简单的图,如下:
把此“图”转换为邻接矩阵的形式,记为
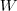
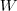
把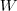
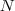

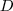
根据拉普拉斯矩阵的定义
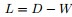 ,可得拉普拉斯矩阵
,可得拉普拉斯矩阵
 为:
为:
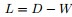 ,可得拉普拉斯矩阵
,可得拉普拉斯矩阵
 为:
为:
2.2 拉普拉斯矩阵的性质
介绍 拉普拉斯矩阵的性质之前,首先定义两个概念,如下:
①对于邻接矩阵,定义图中A子图与B子图之间所有边的权值之和如下:
其中,
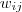 定义为节点
定义为节点
 到节点
到节点
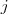 的权值,如果两个节点不是相连的,权值为零。
的权值,如果两个节点不是相连的,权值为零。
②与某结点邻接的所有边的权值和定义为该顶点的度d,多个d 形成一个度矩阵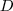 (对角阵)
(对角阵)
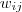 定义为节点
定义为节点
 到节点
到节点
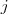 的权值,如果两个节点不是相连的,权值为零。
的权值,如果两个节点不是相连的,权值为零。
②与某结点邻接的所有边的权值和定义为该顶点的度d,多个d 形成一个度矩阵
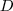 (对角阵)
(对角阵)
拉普拉斯矩阵
 具有如下性质:
具有如下性质:
 具有如下性质:
具有如下性质:
是对称半正定矩阵;
,即
的最小特征值是0,相应的特征向量是
。证明:
*
= (
-
) *
= 0 = 0 *
。(此外,别忘了,之前特征值和特征向量的定义:若数字
和非零向量
满足
,则
为
的一个特征向量,
是其对应的特征值)。
有n个非负实特征值
- 且对于任何一个属于实向量
,有以下式子成立
其中,
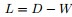 ,
,
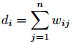 ,
,
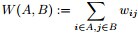 。
。
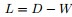 ,
,
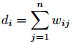 ,
,
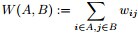 。
。
下面,来证明下上述结论,如下:








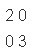

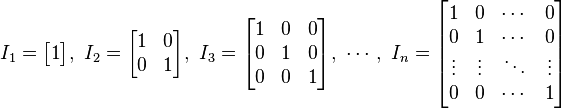
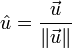
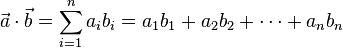
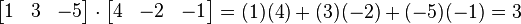
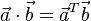
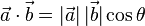



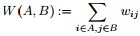
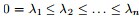
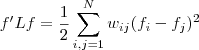
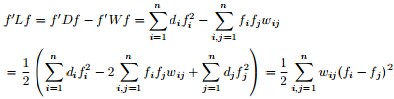














 608
608

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








