打卡信奥刷题（049）用C++信奥P10314[普及组/提高] [SHUPC 2024] 函数Composition

[SHUPC 2024] 函数

题目描述

小 A 正在学习函数，有一天她发现了一个奇妙的函数：
$$f(x)=x-0.5+\frac{\arctan (\cot (\pi x))}{\pi }$$

她非常喜欢这个函数。现在，她会对你提出 $T$ 个询问，每个询问包含一个浮点数 $x$ ，而你只需要回答 $f(x)$ 的值是多少。

选手输出与标准答案的绝对误差或相对误差不超过 $10^{-6}$ 即视为正确。

输入格式

第一行一个整数 $T(T\le 10^4)$ 表示数据组数。

接下来 $T$ 行，每行一个浮点数 $x$ ，保证 $0\le x\le 10^9$ 且 $x\notin \mathbb{N}$（即 $x$ 不为自然数）。

输出格式

输出 $T$ 行，每行一个数，代表答案。

选手输出与标准答案的绝对误差或相对误差不超过 $10^{-6}$ 即视为正确。

样例 #1

样例输入 #1

3
1.10
1.72
2.34

样例输出 #1

1.000000
1.000000
2.000000

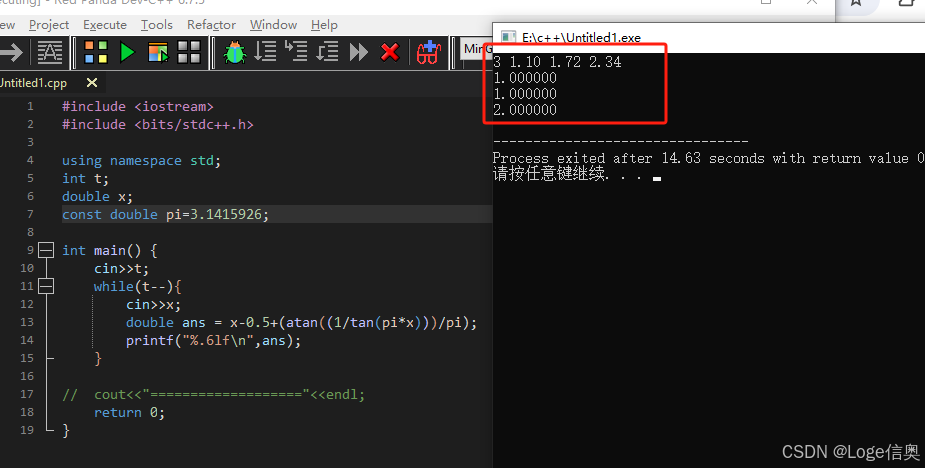
C++实现

#include
#include <bits/stdc++.h>

using namespace std;
int t;
double x;
const double pi=3.1415926;

int main() {
cin>>t;
while(t–){
cin>>x;
double ans = x-0.5+(atan((1/tan(pi*x)))/pi);
printf("%.6lf\n",ans);
}

// cout<<"==================="<<endl;
return 0;
}

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，感兴趣的请关注，我后续将继续分享相关内容