打卡信奥刷题（182）用C++工具信奥P1583[普及组/提高] 魔法照片_一共有 n 个人(以 1 ～ 1～n 编号)向佳佳要照片,而佳佳只能把照片-CSDN博客

魔法照片

题目描述

一共有 $n$ 个人（以 $1∼n1\sim n$ 编号）向佳佳要照片，而佳佳只能把照片给其中的 $k$ 个人。佳佳按照与他们的关系好坏的程度给每个人赋予了一个初始权值 $W_i$ 。然后将初始权值从大到小进行排序，每人就有了一个序号 $D_i$ （取值同样是 $1∼n1\sim n$ ）。按照这个序号对 $10$ 取模的值将这些人分为 $10$ 类。也就是说定义每个人的类别序号 $C_i$ 的值为 $10+1(D_i-1)\bmod 10 +1$ ，显然类别序号的取值为 $\sim 10$ 。第 $i$ 类的人将会额外得到 $E_i$ 的权值。你需要做的就是求出加上额外权值以后，最终的权值最大的 $k$ 个人，并输出他们的编号。在排序中，如果两人的 $E_i$ 相同，编号小的优先。

输入格式

第一行输入用空格隔开的两个整数，分别是 $n$ 和 $k$ 。

第二行给出了 $10$ 个正整数，分别是 $E1∼E10E_1\sim E_{10}$ 。

第三行给出了 $n$ 个正整数，第 $i$ 个数表示编号为 $i$ 的人的权值 $W_i$ 。

输出格式

只需输出一行用空格隔开的 $k$ 个整数，分别表示最终的 $W_i$ 从高到低的人的编号。

样例 #1

样例输入 #1

10 10
1 2 3 4 5 6 7 8 9 10
2 4 6 8 10 12 14 16 18 20

样例输出 #1

10 9 8 7 6 5 4 3 2 1

提示

对于 $100%100\%$ 的数据， $1≤n≤200001\leq n\leq 20000$ ， $1≤k≤n1\leq k\leq n$ ，保证所有数据均在 int 范围之内。

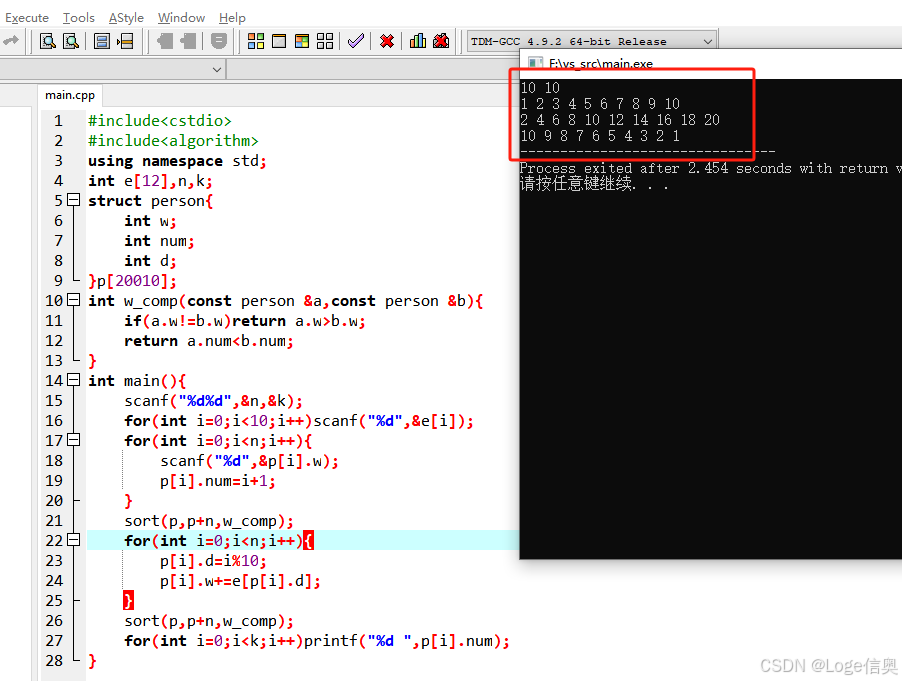
C++实现

#include
#include
using namespace std;
int e[12],n,k;
struct person{
int w;
int num;
int d;
}p[20010];
int w_comp(const person &a,const person &b){
if(a.w!=b.w)return a.w>b.w;
return a.num<b.num;
}
int main(){
scanf(“%d%d”,&n,&k);
for(int i=0;i<10;i++)scanf(“%d”,&e[i]);
for(int i=0;i<n;i++){
scanf(“%d”,&p[i].w);
p[i].num=i+1;
}
sort(p,p+n,w_comp);
for(int i=0;i<n;i++){
p[i].d=i%10;
p[i].w+=e[p[i].d];
}
sort(p,p+n,w_comp);
for(int i=0;i<k;i++)printf("%d ",p[i].num);
}