看图聊算法：超越二分法，探索大厂经典面试题

在上一篇文章的猜数游戏中，我们提到了如下思考题：

看图聊算法：一个游戏让你理解二分法的本质

题目：  你有一个天平和12个小球，其中有一个是假球，但我们不知道它是轻还是重。你至少需要称重多少次来确定哪个是假球？

这实际上是大厂面试中的经典问题。我曾经困惑，为什么一个益智题会出现在技术面试里，而且它似乎与技术无关。

但经过深入探究，我了解到这种题目的真正考察点。它旨在测试你是否能够灵活运用技术的核心原理，并在需要时迅速想到相应的解决方法。

试错法

现在回到这道题目，给自己几分钟思考一下，该如何称重？

为了解答这个问题，你或许会想到不断地进行试错，然后从中总结方法。

例如，你可以将球分成两组，称重后发现不能确定哪组包含假球。接下来，你再将它们分成四组，两两称重，从而确定有两组球是正常的，并与另两组比较……

这种方法虽然最终可以找到假球，但题目要求的是用最少的称重次数找出假球。

那如何确定你的方案是最优的呢？一个可能的方法是尝试多种方案，然后选取称重次数最少的。

你是不是会感觉这个方法有些不靠谱？

归约法

回想我们之前讨论的猜数字游戏，其中证明了二分法是猜数字的最优策略。

从猜数字游戏出发，我们提出了解决搜索问题的策略：

1. 定义解空间；

2. 基于问题特性减小解空间。

我们尝试一下，是否可以将此策略应用于称球问题。

解空间

在 0-31 的猜数游戏中，答案可能是这个区间内的任何数字，因此解空间有 32 个可能。

在称球问题中，假球可能是 12 个中的任何一个，共 12 种可能。考虑到假球可能是轻或重，总的解空间就有 12*2 = 24 种可能。

我们用 + 表示球重，用 - 表示球轻。

轻或重

24 种可能的解空间：

解空间 24 种可能

基于问题特性减小解空间

在猜数游戏中，回答只能是“是”或“否”，因此最优的策略是通过一个问题，将解空间的可能性减小一半。

那么在称球问题中，我们如何来有效地减少解空间呢?

天平可以提供三种结果：左边重、等重或右边重，也就是说一个问题有三种答案的可能。因此，根据猜数游戏的启发，我们最优的策略是每次都将解空间三等分。

也就是说，每次都可以将解空间的可能性减小 1/3。那么“最少需要多少次称重”的问题就变为：“3 的多少次方 >=24 且最接近 24？”

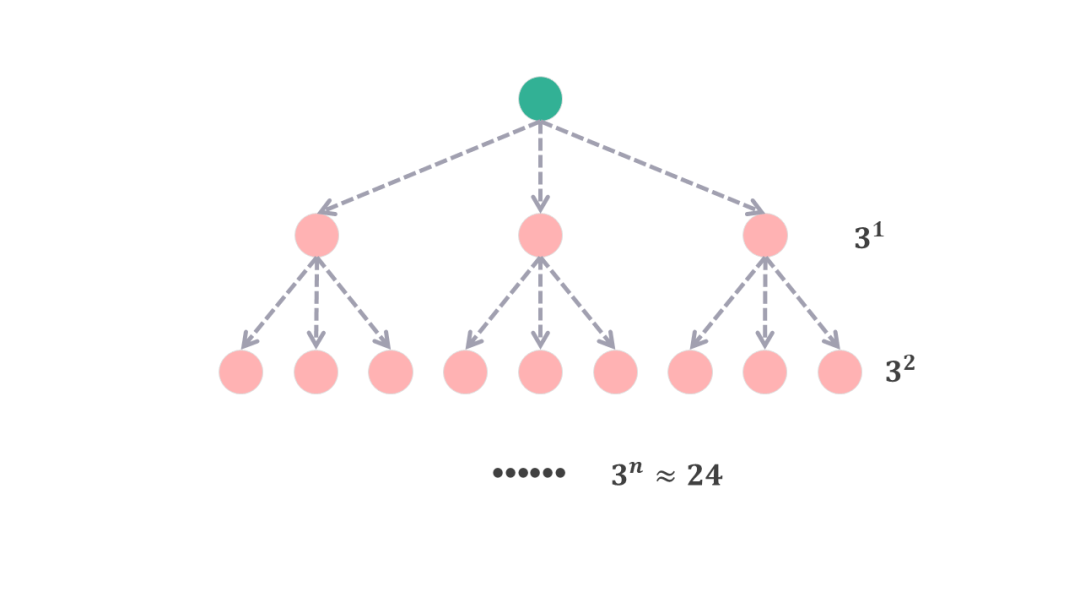
答案是 3 次，因为 3^3 = 27，最接近 24。

有了这个结论，如何来验证？我们不妨一步步试一下。

1. 第一步

第一步，我们要将 12 个球分为三组：A 组包括“1、2、3、4”；B 组包括“5、6、7、8”；C 组则包括“9、10、11、12”。

接下来，我们把 A 组“1、2、3、4”（左边）与 B 组“5、6、7、8”（右边）放在天平两侧进行称重。

• 若左边更重，那么有两种可能：要么假球重且位于 A 组中，解空间为“1+、2+、3+、4+”；要么假球轻且位于 B 组中，解空间为“5-、6-、7-、8-”。

• 若两边等重，则表明 A 组和 B 组的球都是正常的，假球则在 C 组中。这时假球可能是轻的，解空间为“9-、10-、11-、12-”，或者是重的，解空间为“9+、10+、11+、12+”。

• 若右边更重，则与左边更重的情况恰好相反。这时可能的情况是假球重且位于 B 组中，解空间标记为“5+、6+、7+、8+”，或者假球轻且位于 A 组中，解空间标记为“1-、2-、3-、4-”。

第一步

仅通过一次称重，我们就已经将解空间三等分，每等分只要 8 (24 除以 3) 种可能的解空间。

2. 第二步

第二步，以第一步中“左边更重”为例，此时的解空间为：“1+，2+，3+，4+”与“5-，6-，7-，8-”。

接下来，我们选取“1，2，6”放于天平的左边，而“3，4，5”则放在右边进行称重。

• 若左边更重，那么有两种可能性：要么假球较重并位于“1+，2+”中；要么假球较轻，且为“5-”。

• 若天平两端平衡，则说明这两边的球都是正常的。这样，未被称重的球中就隐藏着那颗假球，“7-，8-”。

• 若右边更重，那么假球可能较重并位于“3+，4+”中，或者假球较轻，正是“6-”。

第二步

此轮称重后，我们又进一步缩小了假球的潜在范围。

3. 第三步

第三步，我们继续以第二步中的“左侧较重”情境为基础，此刻面临的解空间缩减为：“1+，2+，5-”。

现在，将“1”置于天平左侧，而“2”则放在右侧进行称重。

• 若左侧更重，那么明确假球是较重的，“1+”。

• 若天平两端平衡，则这两侧的球均正常。因此，未进行称重的那颗球即为假球，“5-”。

• 若右侧更重，那么可以确定假球是重的，“2+”。

第三步

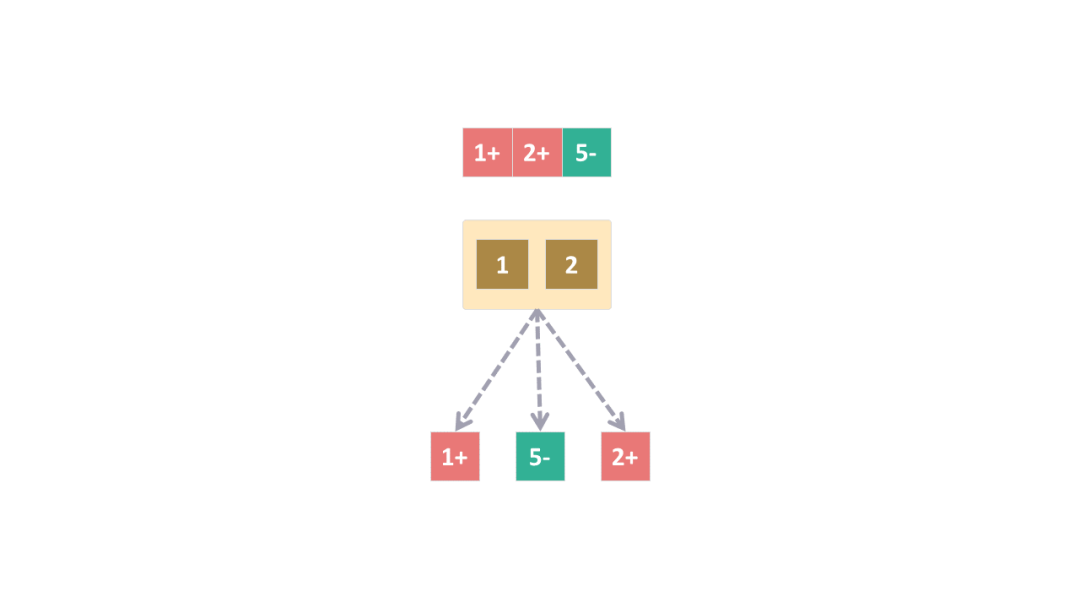
只需三次称重，我们便锁定了那颗不合群的假球。

称球问题图解

尽管我们上文中每次只走了其中一条分支，但三次称重后的所有可能答案，都在下图中清晰地展示。

称球问题图解

总结

当我们解答了整个问题后，不禁要问：为什么技术面试偏爱这类锻炼思维的益智题？

面试这样的题目，其实更多的是看你面对问题时，是否能够抽象思考，从深层次发现其本质。

回想猜数游戏，二分法似乎是显而易见的答案。但真正的挑战是：我们是否能够将这种思维方式抽象出来，应用于更广泛的问题呢？这并非易事。

面对问题，我们的首要任务是剥去外部的干扰，对其进行抽象，直达问题的本质。

现在，我们已经掌握了解决搜索问题的策略：

1. 定义解空间；

2. 基于问题特征减小解空间。

接下来，我们可以深入讨论一个更具技术性的问题：为何比较排序的最佳时间复杂度是 O(nlogn)。

本文参考资料：

1. http://mindhacks.cn/2008/06/13/why-is-quicksort-so-quick/
2. https://www.inference.org.uk/itprnn/book.pdf

---

WWH 系列文章列表：

[1] Why - 为什么 JS 更像一门编译型语言？

[2] What - 什么是依赖注入？

[3] What - 什么是 Big O？

[4] How - 不同的语言都如何处理错误？

[5] How - 面向对象语言如何处理异常？

最近文章列表：

[1] 计算机诞生之前，数据如何排序？

[2] 人生有没有意义？人类又有什么意义？

[3] 第一性原理

[4] 什么是好奇心？

[5] 需要多少内存来运行100万个并发任务？

[6] 在 C 语言中实现简单的哈希表

[7] 成就卓越：事业成功的核心要素

[8] PPT 发展简史

[9] C++异常处理的底层机制

[10] 看图聊算法：一个游戏让你理解二分法的本质

喜欢本篇文章，记得动动小手点个在看↓↓