Crashing Robots
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 11677 | Accepted: 4952 |
Description
In a modernized warehouse, robots are used to fetch the goods. Careful planning is needed to ensure that the robots reach their destinations without crashing into each other. Of course, all warehouses are rectangular, and all robots occupy a circular floor space with a diameter of 1 meter. Assume there are N robots, numbered from 1 through N. You will get to know the position and orientation of each robot, and all the instructions, which are carefully (and mindlessly) followed by the robots. Instructions are processed in the order they come. No two robots move simultaneously; a robot always completes its move before the next one starts moving.
A robot crashes with a wall if it attempts to move outside the area of the warehouse, and two robots crash with each other if they ever try to occupy the same spot.
A robot crashes with a wall if it attempts to move outside the area of the warehouse, and two robots crash with each other if they ever try to occupy the same spot.
Input
The first line of input is K, the number of test cases. Each test case starts with one line consisting of two integers, 1 <= A, B <= 100, giving the size of the warehouse in meters. A is the length in the EW-direction, and B in the NS-direction.
The second line contains two integers, 1 <= N, M <= 100, denoting the numbers of robots and instructions respectively.
Then follow N lines with two integers, 1 <= Xi <= A, 1 <= Yi <= B and one letter (N, S, E or W), giving the starting position and direction of each robot, in order from 1 through N. No two robots start at the same position.
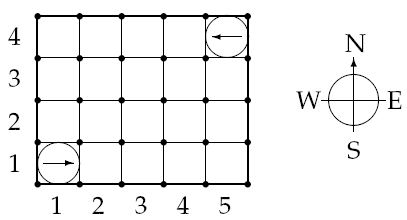
Figure 1: The starting positions of the robots in the sample warehouse
Finally there are M lines, giving the instructions in sequential order.
An instruction has the following format:
< robot #> < action> < repeat>
Where is one of
and 1 <= < repeat> <= 100 is the number of times the robot should perform this single move.
The second line contains two integers, 1 <= N, M <= 100, denoting the numbers of robots and instructions respectively.
Then follow N lines with two integers, 1 <= Xi <= A, 1 <= Yi <= B and one letter (N, S, E or W), giving the starting position and direction of each robot, in order from 1 through N. No two robots start at the same position.

Figure 1: The starting positions of the robots in the sample warehouse
Finally there are M lines, giving the instructions in sequential order.
An instruction has the following format:
< robot #> < action> < repeat>
Where is one of
- L: turn left 90 degrees,
- R: turn right 90 degrees, or
- F: move forward one meter,
and 1 <= < repeat> <= 100 is the number of times the robot should perform this single move.
Output
Output one line for each test case:
Only the first crash is to be reported.
- Robot i crashes into the wall, if robot i crashes into a wall. (A robot crashes into a wall if Xi = 0, Xi = A + 1, Yi = 0 or Yi = B + 1.)
- Robot i crashes into robot j, if robots i and j crash, and i is the moving robot.
- OK, if no crashing occurs.
Only the first crash is to be reported.
Sample Input
4 5 4 2 2 1 1 E 5 4 W 1 F 7 2 F 7 5 4 2 4 1 1 E 5 4 W 1 F 3 2 F 1 1 L 1 1 F 3 5 4 2 2 1 1 E 5 4 W 1 L 96 1 F 2 5 4 2 3 1 1 E 5 4 W 1 F 4 1 L 1 1 F 20
Sample Output
Robot 1 crashes into the wall Robot 1 crashes into robot 2 OK Robot 1 crashes into robot 2
Source
解题思路:
明显的模拟题,输入输出稍有点复杂,将四个方向抽象成四个坐标(1,0)(-1,0)(0,1)(0,-1)
然后利用模拟的思想对题目进行求解:
#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
typedef struct node
{
int x,y,dir;
}robit;
robit r[110];
bool s[110][110];
int dir[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
int a,b,n,m;
int num[110],rep[110];
char act[110];
bool judge(int x,int y)
{
if(x<1||x>a||y<1||y>b)
return true;
return false;
}
void solve()
{
int x,y;
for(int i=1;i<=m;i++)
{
bool flag=true;
if(act[i]=='F')
{
s[r[num[i]].x][r[num[i]].y]=false;
while(rep[i]--)
{
x=r[num[i]].x+dir[r[num[i]].dir][0];
y=r[num[i]].y+dir[r[num[i]].dir][1];
if(judge(x,y))
{
printf("Robot %d crashes into the wall\n",num[i]);
flag=false;
break;
}
if(s[x][y])
{
int k;
for(k=1;k<=n;k++)
if(r[k].x==x&&r[k].y==y) break;
printf("Robot %d crashes into robot %d\n",num[i],k);
flag=false;
break;
}
r[num[i]].x=x;
r[num[i]].y=y;
r[num[i]].dir=r[num[i]].dir;
}
s[x][y]=true;
}
rep[i]%=4;
if(act[i]=='R')
while(rep[i]--)
{
int mov=r[num[i]].dir-1;
if(mov==-1) mov=3;
r[num[i]].dir=mov;
}
if(act[i]=='L')
while(rep[i]--)
{
int mov=r[num[i]].dir+1;
if(mov==4) mov=0;
r[num[i]].dir=mov;
}
if(!flag) break;
if(i==m) printf("OK\n");
}
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
char ch;
memset(s,0,sizeof(s));
scanf("%d%d",&a,&b);
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
cin>>r[i].x>>r[i].y>>ch;
s[r[i].x][r[i].y]=true;
if(ch=='E') r[i].dir=0;
if(ch=='N') r[i].dir=1;
if(ch=='W') r[i].dir=2;
if(ch=='S') r[i].dir=3;
}
for(int i=1;i<=m;i++)
cin>>num[i]>>act[i]>>rep[i];
solve();
}
return 0;
}




 本文介绍了一个典型的机器人路径模拟问题——避免碰撞。通过定义机器人的初始位置、方向及一系列指令,确保机器人在限定区域内移动时不会发生碰撞。文章提供了一种解决方案,采用结构化的数据存储方式和详细的逻辑判断来实现。
本文介绍了一个典型的机器人路径模拟问题——避免碰撞。通过定义机器人的初始位置、方向及一系列指令,确保机器人在限定区域内移动时不会发生碰撞。文章提供了一种解决方案,采用结构化的数据存储方式和详细的逻辑判断来实现。
















 107
107

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








