＜ Introduction to Algorithms ＞( 理论，时空复杂度，数学函数，数学基础 )

森龙安

已于 2024-09-24 15:00:33 修改

阅读量659

点赞数 7

分类专栏：数据结构与算法数学文章标签：算法

于 2024-09-02 16:23:04 首次发布

本文链接：https://blog.csdn.net/sengyongan/article/details/141818457

版权

数据结构与算法同时被 2 个专栏收录

6 篇文章 0 订阅

订阅专栏

数学

4 篇文章 0 订阅

订阅专栏

理论

数据结构：存储和组织数据的方式，旨在便于访问和修改

算法：解决问题的方式，把输入转换为输出的计算步骤，任何具有明确的步骤或规则的代码片段，用于旨在高效、准确地解决特定问题。

设计模式：帮助开发者结构化和组织代码，提高代码的可维护性、可扩展性和复用性。

提取

$eq?%5Csum$ Θ $\bigcup$ $\Phi$ $\bowtie$ $\pi$ $\vee$ $\wedge$ $\delta$ $\Delta$ $\Omega$

渐进记号

应用于函数，用来表示算法的运行时间或使用的空间数量，根据输入自然数集n来定义

Θ（西塔）记号的数学定义：

渐进紧缺界——输入运行时间

Θ(g(n)) = { f(n) : 存在正常量 c1、c2 和 n0，使得对所有 n ≥ n0，有 0 （时间为正）≤ c1g(n) ≤ f(n) ≤ c2g(n) }

这里的g(n)表示一个多项式非形式化表示（比如n，n^2，log n，2^n……）
正常量 c1、c2 应用与g(n)，c1g(n) 和c2g(n)表示上下界，
n是输入规模，n0作为阈值
Θ(g(n))表示一个集合，如果f(n)是所有满足条件的函数，属于集合，g(n)是f(n)的渐进紧缺界（<=或>=)（渐进下界和渐进上界）

我们可以忽略掉低阶项以及高阶项的系数，如何证明？

方法一：

可以通过一个2次函数1/2 n^2 - 3n =（属于）Θ(n^2)，这里的n^2即为2次函数的非形式化表示

我们需要证明1/2 n^2 - 3n属于Θ(n^2)，首先确定两个正常量c1、c2，然后就能确定no，从而证明成立，但如果我们无法有上述选择，则2次函数不属于Θ(n^2)

可证，当c2>=1/2 , c1<=1/14, no=7时，条件成立

方法二；反证法

可以用比如3次函数6n^3是否 = （属于）Θ(n^2)，

可以简单假设c2和no , 6n^3 <= c2n^2 ,简化后 n <= c2 / 6,因为c2为常量（不变的量）如果n比较大上述不可能成立，因此可证条件不满足

如何通俗理解记号？

Θ(g(n))表示非形式化的算法时间，即所有满足条件（ 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n)）的函数，即满足渐进紧确界（上界，下界）的函数（f(n)即以输入规模n作为变量的多项式），都可以用Θ(g(n))表示

Θ(n^0) 或 Θ(1)常量表示，满足Θ(1)的函数都是0阶的多项式，不随输入规模 n 的增长而增长

O（大欧）记号的数学定义：

渐进紧确上界——最坏运行时间

O(g(n)) = { f(n) : 存在正常量 c和 n0，使得对所有 n ≥ n0，有 0 ≤ f(n) ≤ cg(n) }

Θ(g(n)) $\sqsubseteq$ O(g(n))

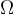$\Omega$ （大欧米伽）记号的数学定义：

Θ(g(n)) = { f(n) : 存在正常量 c 和 n0，使得对所有 n ≥ n0，有 0 ≤ cg(n) ≤ f(n) }

渐进紧确下界——最好运行时间

o（小欧）非渐进紧确上界（非<=)

是严格上限，不可以==

w（小欧米伽）非渐进紧确下界（非>=)

渐进记号的性质

传递

自反

对称

转置对称

类似于实数ab的比较

多项式非形式化g(n)表示

去掉运行时间中的加法常数项
忽略掉低阶项以及高阶项的系数
只保留保留最高项，去掉低阶项

记号和等式

f(n) = O(g(n)),， =号表示属于

T(n) = 2T(n/1) + O(n)，，O(n)出现在=右边公式内表示匿名函数（低阶项），

2n^2 + O(n) = O(n^2 ),出现在=左边公式内匿名函数,比右边更细节

常见的O(g(n))函数——时间

O（1）常数时间，算法的运行时间不依赖于输入规模
O(log n)对数时间，二分查找等分治算法
O(n)线性时间（多项式），归并排序、快速排序
O(n * log n)线性对数时间，速度较快，简单的线性查找或遍历
O(n^2)平方时间，速度较慢，冒泡排序、选择排序。
O(n^3)立方时间：通常是三重嵌套循环
O(2^n)指数时间,暴力解法、某些递归算法
O(n！)速度非常慢,暴力解法（旅行商问题）

常见的O(g(n))函数——空间

描述了算法在输入规模增加时，所需的存储空间的增长情况。考虑程序运行时占用内存的大小，而不是可执行文件的大小。

O(1)常数空间，只使用有限个变量，不额外申请空间
O(n)线性空间，需要额外数组或链表来存储输入数据。
O(n2)平方空间，需要一个二维数组来存储数据。

数学函数

多项式

函数p(n) = (i=0;i<=d) $eq?%5Csum$ ai n^i,

表示n的d次多项式（我们知道几次多项式都是根据最高次项决定）

ai是系数

当a>=0， n^a单调递增

a<=0 ， n^a单调递减

指数

a^n(a>0),

当a>=1时单调递增

任意底数a>1的指数函数比多项式增长快的多

自然对数e （欧拉数）= 2.71828…… = （i=0;i< $\bowtie$ ) $eq?%5Csum$ x^i / i!

对数

幂：一个数被多次相同的数相乘的结果：底数a^指数b，a 自身乘以自身 b 次

对数：指数的逆运算：给定一个幂的结果，求底数需要多少次方才能得到这个结果

转换：logb(x) = y -> b^y = x(b>0)

以 e 为底的对数，记作 ln⁡, 以 10 为底的对数，记作 log

对数 < 多项式 < 指数

阶乘

递归是指在定义或解决问题时，函数直接或间接地调用自己。递归可以简化代码层面的复杂度，而非时间空间复杂度

递归时间复杂度：递归的次数 * 每次递归中的操作次数。

当n=0时,n! =1,,n>0时，n! = n * (n-1)

阶乘：一个正整数的所有小于或等于该数的正整数的乘积

w(2^n) < n! < o(n^n)是极大的时间

int function2(int x, int n) {
    if (n == 0) {
        return 1; 
    }
    return function2(x, n - 1) * x;
}

多重函数表示

f^(i) (n)表示f(n)重复i次作用于初始值

斐波那契数

斐波那契数:，F(0)=0,F(1)=1，F(i) = F(i-1)+F(i-2)

int fibonacci(int i) {
       if(i <= 0) return 0;
       if(i == 1) return 1;
       return fibonacci(i-1) + fibonacci(i-2);
}

黄金分割率 φ（phi）：1.61803……

共轭数 $\delta$ := -0.61803……

数学基础

单调性

m <= n f(m) <= f(n) 单调递增， f(m) >= f(n) 单调递减

m < n f(m) < f(n) 严格递增， f(m) > f(n) 严格递减（因为不可以==，所以范围更严格）

a>=0时，n^a单调递增,a<=0时，n^a单调递减,

向下取整向上取整

向下取整： $\coprod$ 表示<=x的最大整数

向上取整： $\prod_{}^{}$ 表示>=x的最小整数

性质 $\coprod$ n/2 + $\prod_{}^{}$ n/2 = n，例如3/2 = 1.5 -> 1+2 = 3

无论 $\coprod$ 还是 $\prod_{}^{}$ 都是单调递增

不等式

题目1：

y = (x^2 - x + 4) /（ x - 1）求在x>1条件下y最小值

解：

首先化简y = (x−1) + （4 /（x−1））+1，

根据基本不等式公式，可以求出y的范围：(a+b)/2 >= $\vee$ ab , 将(x−1)作为a，将 4 /（x−1）作为b，求得(x−1) + （4 /（x−1））>=4, (x−1) + （4 /（x−1））+1>=5,

当结果为最小值5时，x为3，满足x>1因此，最小值为5

题目2：

c1<=1/2 - 3/n,已知c1<=1/14，则 n恒成立范围

可以将c1=1/14，带入不等式，求得n>=7，

为什么取最大值？因为当n>=7时，右边结果>=c1,当c1取更小的值，右边结果也依旧>=c1

求和

集合

笛卡尔积（Cartesian product）：集合A和B，A和B的笛卡尔积是一个集合，其中的元素是所有可能的(a, b)对

例如，如果有集合A = {1, 2}和B = {3, 4}，那么A和B的笛卡尔积A × B = {(1,3), (1,4), (2,3), (2,4)}。

有限集：有限的集合

计数

和规则：

应用于不相交集合（不相关），我选择一个，就无法选择另一个集合，通过两个集合元素数目求和，统计有多少种可能的选择方式

积规则：

应用于相交集合，选择集合1某一个，同时选择集合2某个的，通过两个集合元素数目相乘，统计有多少种可能的选择方式

串：

集合中的子序列，即连续若干个元素的有序序列，长度为k的串，称为k串，是整个集合序列的子串

如果想要在集合N中构造长度为k的串，N元素数量为n，求多少种可能的构成方式？

串的每个元素都有n中选择，我需要同时选择这些元素，因此需要利用积规则，即n^k

排列：

有限集S的排列：元素的有序序列，对于每种排列方式，每个元素仅出现一次

给定有限集S，元素数量为n，求排列数目？

第一个元素有n中选择，因为每个元素仅出现一次，我第二次无法选择这个元素，因此有n-1种选择，以此类推，并使用积规则，恰好符合n!

给定有限集S，元素数量为n，求k排列数目？

这次排列并非整个序列，而是长度为k的序列，当到第k个元素时，有n-k+1种可能，因此n(n-1)(n-2)……(n-k+1) = n! / (n-k)! (因为展开后上下抵消）

组合：

有限集S的k组合：属于s的子集，但是元素的顺序对组合没有影响

求k组合数目？

可以用k排列，表示k组合，每个组合对应k!个元素排列，因此 = n! / (n-k)! * k!

二项系数:

读作n选k，表示集合n种k组合的数目

概率

样本空间S是基本事件的集合{，，，}，每个事件是一个子集，是一种结果

必然事件：在一定条件下，一定会发生的事件

空事件：在一定条件下，绝对不会发生的事件

互斥事件：是指两个或多个事件，它们在同一次试验中不能同时发生，也就是集合交集为空

概率分布：

从事件到实数的映射

Pr{A}：事件A的概率分布>=0，也称为事件A的概率

Pr{Null} = 0

Pr{S-A} = 1 - Pr{A}

对于任意两个集合：Pr{A $\bigcup$ B) = Pr{A} + Pr{B} + Pr{A $\bigcap$ B}

对于两个独立事件：

Pr{A $\bigcup$ B) = Pr{A} + Pr{B}

Pr{A $\bigcap$ B} = 算{}内事件占总体的概率

均匀概率：

每个子事件发生的概率都为 1/ 总基本事件

事件A中基本事件概率和 / 所有基本事件概率和，其中A中每个基本事件

比如：

一枚硬币的事件为均匀事件，总共有两种（正反）基本事件，均匀性：每个事件都是1/2的概率，

如果抛n次，那么根据积规则计数方式，所有可能的组合方式为2^n

正或反的基本事件的概率为1/2^n

条件概率

B条件下A的概率，

例如：已知抛两枚均匀硬币，其中已知一枚硬币证明向上，问两个都正面向上的概率

ab同时发生的概率为1/4,b发生的概率为3/4，所以概率为1/3

离散随机变量

随机变量X：样本到实数的函数，假定随机变量是离散的

例如一对骰子有36个基本事件，每个基本事件s为 1 / 36 ，比如{1,3},{2,3}这样的基本事件，其中当x==3时，概率为5/36，

随机变量X的期望值(均值）E[X]:

数论

研究整数的性质以及整数之间的关系

整除与约数：
- 如果整数a除以整数b（b≠0）的余数为0，则称a能被b整除，记作b|a。
- 如果b|a，则称b是a的约数（或因数），a是b的倍数。
最大公约数与最小公倍数：
- 两个或多个整数共有的最大的能整除它们的正整数称为它们的最大公约数（GCD）。
- 两个或多个整数的公共倍数中最小的一个称为它们的最小公倍数（LCM）。
质数与合数：
- 一个大于1的自然数，除了1和它本身以外不再有其他因数的数称为质数（素数）。
- 不是质数的正整数称为合数。
算术基本定理：
- 任何一个大于1的自然数n都可以唯一地分解为有限个质数的乘积，即 n=p1e1p2e2⋯pkek，其中 p1,p2,…,pk 是质数，且 e1,e2,…,ek 是正整数。
同余与模运算：
- 如果两个整数a和b被某个正整数m除后余数相同，则称a和b模m同余（等价， $\not\equiv$ 不等价），记作 a≡b(modm)。
- 模运算是一种在整数集合上定义的运算，其结果是一个整数除以另一个整数后的余数。
- 取余：amodn = a - n $\coprod$ (a/n)我们指定程序中的除法都是默认向下取整的
- 0 < amodn < n
欧拉定理与费马小定理：
- 欧拉定理：如果a和n是互质的正整数，那么 aφ(n)≡1(modn)，其中 φ(n) 是欧拉函数，表示小于n且与n互质的正整数的个数。
- 费马小定理：如果p是一个质数，a是一个整数且p不整除a，那么 ap−1≡1(modp)。费马小定理是欧拉定理的一个特例。
二次剩余与二次互反律：
- 二次剩余：给定一个整数p（p是奇质数）和一个整数a，如果存在整数x使得 x2≡a(modp)，则称a是模p的二次剩余。
- 二次互反律：是关于模p的二次剩余的一个深刻定理，它给出了模p和模q的二次剩余之间的一个关系，其中p和q是不同的奇质数。

论证方式

每一步的推理都是基于已知事实或先前已证明的命题，目的证明新的命题是否成立

直接证明：
- 直接从已知事实或先前已证明的命题（前提）出发，通过一系列的逻辑推理，最终推导出要证明的结论。
反证法（归谬法）：
- 首先假设相反命题是成立的，然后通过逻辑推理，推导出与已知事实或先前已证明的命题相矛盾的结论。由于矛盾的存在，说明假设是错误的，从而证明了原结论的正确性。
数学归纳法：
- 它包括两个步骤：基础步骤（验证当n=1时命题成立）和归纳步骤（假设当n=k时命题成立，然后证明当n=k+1时命题也成立）。如果这两个步骤都能成功完成，那么就可以断定对于所有的自然数n，该命题都成立。