Bessel's inequality
In mathematics, especially functional analysis, Bessel's inequality is a statement about the coefficients of an element  in a Hilbert space with respect to an orthonormal sequence.
in a Hilbert space with respect to an orthonormal sequence.
Let  be a Hilbert space, and suppose that
be a Hilbert space, and suppose that  is an orthonormal sequence in
is an orthonormal sequence in  . Then, for any
. Then, for any  in
in  one has
one has
where 〈•,•〉 denotes the inner product in the Hilbert space  . If we define the infinite sum
. If we define the infinite sum
consisting of 'infinite sum' of vector resolute  in direction
in direction  , Bessel's inequality tells us that this series converges. One can think of it that there exists
, Bessel's inequality tells us that this series converges. One can think of it that there exists 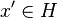 which can be described in terms of potential basis
which can be described in terms of potential basis  .
.
For a complete orthonormal sequence (that is, for an orthonormal sequence which is a basis), we have Parseval's identity, which replaces the inequality with an equality (and consequently 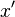 with
with  ).
).
Bessel's inequality follows from the identity:
which holds for any natural n.
Statement of the inequality[edit]
The Cauchy–Schwarz inequality states that for all vectors x and y of an inner product space it is true that
where 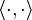 is the inner product also known as dot product. Equivalently, by taking the square root of both sides, and referring to the norms of the vectors, the inequality is written as
is the inner product also known as dot product. Equivalently, by taking the square root of both sides, and referring to the norms of the vectors, the inequality is written as
Moreover, the two sides are equal if and only if x and y are linearly dependent (or, in a geometrical sense, they are parallel or one of the vectors' magnitude is zero).
If  and
and  have an imaginary component, the inner product is the standard inner product and the bar notation is used for complex conjugation then the inequality may be restated more explicitly as
have an imaginary component, the inner product is the standard inner product and the bar notation is used for complex conjugation then the inequality may be restated more explicitly as
When viewed in this way the numbers x1, ..., xn, and y1, ..., yn are the components of x and y with respect to an orthonormal basis of V.
Even more compactly written:
Equality holds if and only if x and y are linearly dependent, that is, one is a scalar multiple of the other (which includes the case when one or both are zero).
The finite-dimensional case of this inequality for real vectors was proven by Cauchy in 1821, and in 1859 Cauchy's student Bunyakovsky noted that by taking limits one can obtain an integral form of Cauchy's inequality. The general result for an inner product space was obtained by Schwarz in the year 1888.
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces.
- Theorem (Hölder's inequality). Let (S, Σ, μ) be a measure space and let p, q ∈ [1, ∞] with 1/p + 1/q = 1. Then, for all measurable real- or complex-valued functions f and g on S,
- If, in addition, p, q ∈ (1, ∞) and f ∈ Lp(μ) and g ∈ Lq(μ), then Hölder's inequality becomes an equality if and only if |f |p and |g |q are linearly dependent in L1(μ), meaning that there exist real numbers α, β ≥ 0, not both of them zero, such that α |f |p = β |g|q μ- almost everywhere.
The numbers p and q above are said to be Hölder conjugates of each other. The special case p = q = 2 gives a form of the Cauchy–Schwarz inequality. Hölder's inequality holds even if ||fg||1 is infinite, the right-hand side also being infinite in that case. Conversely, if f is in Lp(μ)and g is in Lq(μ), then the pointwise product fg is in L1(μ).
Hölder's inequality is used to prove the Minkowski inequality, which is the triangle inequality in the space Lp(μ), and also to establish thatLq(μ) is the dual space of Lp(μ) for p ∈ [1, ∞).








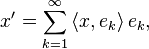

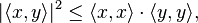
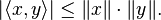
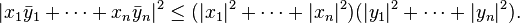
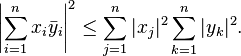
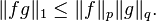













 2657
2657











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








