基本概念
- 复指数集包括连续时间的
est
e
s
t
和离散时间信号的
zN
z
N
信号,其中
s
s
和都是复数.一般来说,
s
s
和可以是任意复数,但傅里叶分析仅限于这些变量的特殊形式.
- 在连续时间情况下仅涉及 s s 的纯虚部值,即,因此仅考虑 ejwt e j w t 形式的复指数.
- 在离散时间情况下仅限于单位振幅的 z z 值,即,因此仅考虑 ejwn e j w n 形式的复指数.
线性时不变系统对复指数信号的响应
在研究线性时不变系统时,将信号表示为基本信号的线性组合是有利的,这些基本信号应该具有以下两个性质.
- 有这些基本信号能够构成相当广泛的一类有用信号
- 线性时不变系统对每一个基本信号的响应应该十分简单,以使系统对任意输入信号的响应有一个很方便的表达式
连续和离散时间信号集都具有上述两个性质,即连续时间的 est e s t 和离散时间信号的 zN z N 信号,其中 s s 和都是复数.
- 在研究线性时不变系统时,复指数信号的重要性在于这样一个事实.即一个线性时不变系统对复指数信号的响应也是同样一个复指数信号,不同的只是幅度上的变换,即
est→H(s)estzN→H(z)zN(1) (1) e s t → H ( s ) e s t z N → H ( z ) z N
其中 H(s) H ( s ) 或 H(z)) H ( z ) ) 是一个复振幅因子,一般来说是复变量 s s 或的函数.
对公式(1)的证明如下
- 连续时间系统,其单位冲激响应为
h(t)
h
(
t
)
,输入
x(t)=est
x
(
t
)
=
e
s
t
y(t)=∫+∞−∞h(τ)x(t−τ)dτ=∫+∞−∞h(τ)es(t−τ)dτ=est∫+∞−∞h(τ)e−sτdτ(1)(2)(3) (1) y ( t ) = ∫ − ∞ + ∞ h ( τ ) x ( t − τ ) d τ (2) = ∫ − ∞ + ∞ h ( τ ) e s ( t − τ ) d τ (3) = e s t ∫ − ∞ + ∞ h ( τ ) e − s τ d τ
令 H(s)=∫+∞−∞h(τ)e−sτdτ H ( s ) = ∫ − ∞ + ∞ h ( τ ) e − s τ d τ ,假定 H(s) H ( s ) 收敛,于是系统对 est e s t 的响应为
y(t)=H(s)est y ( t ) = H ( s ) e s t
其中 H(s) H ( s ) 是一个常复数,其值决定于 s s . - 离散时间系统,其单位冲激响应为,输入
x(n)=zn
x
(
n
)
=
z
n
y(n)=∑k=−∞+∞h(k)x(n−k)=∑k=−∞+∞h(k)zn−k=∑k=−∞+∞znh(k)z−k(4)(5)(6) (4) y ( n ) = ∑ k = − ∞ + ∞ h ( k ) x ( n − k ) (5) = ∑ k = − ∞ + ∞ h ( k ) z n − k (6) = ∑ k = − ∞ + ∞ z n h ( k ) z − k
令 H(z)=∑+∞k=−∞h(k)z−kdτ H ( z ) = ∑ k = − ∞ + ∞ h ( k ) z − k d τ ,假定 H(z) H ( z ) 收敛,于是系统对 zn z n 的响应为
y(n)=H(z)zn y ( n ) = H ( z ) z n
其中 H(z) H ( z ) 是一个常数,其值决定于 z z .
连续时间傅里叶级数
- 连续时间周期信号的傅里叶级数表示
- 傅里叶级数的收敛
- 问题引出:对于任何周期信号,总能求得一组 ak a k .然而,在某些情况下, ak a k 求得的值可能是无限大,导致求得的 x(t) x ( t ) 不收敛.
- 对于大部分周期信号而言不存在不收敛问题. 如果一个周期信号满足如下条件,就能保证该信号可用傅里叶级数表示.
- 在任何周期内,
x(t)
x
(
t
)
必须绝对可积,即
∫T|x(t)|<∞ ∫ T | x ( t ) | < ∞
这一条件保证了每一系数 ak a k 都是有限值, - 在任意区间内, x(t) x ( t ) 具有有限个起伏变化;也就是说,在任何单个周期内, x(t) x ( t ) 的最大值和最小值的数目有限.
- 在 x(t) x ( t ) 的任何有限区间内,只有有限个不连续点,而且在这些不连续点上,函数是有限值.
- 在任何周期内,
x(t)
x
(
t
)
必须绝对可积,即
- 傅里叶级数的收敛
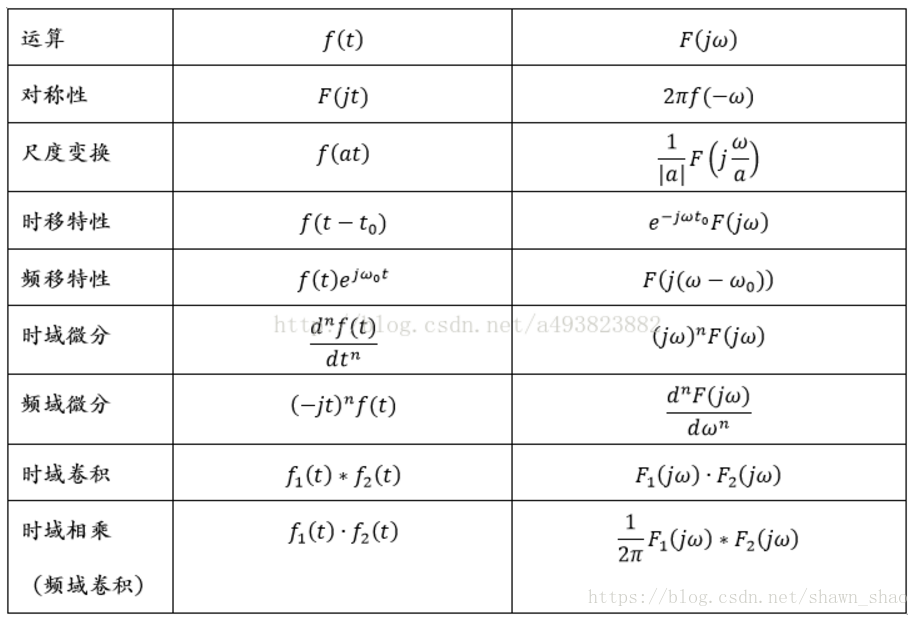
连续时间傅里叶级数性质
部分性质证明
- 时移性质
ak=1T∫Tx(t)e−jkw0tdt=1T∫Tx(t)e−jk(2π/T)tdt a k = 1 T ∫ T x ( t ) e − j k w 0 t d t = 1 T ∫ T x ( t ) e − j k ( 2 π / T ) t d t
bk=1T∫Tx(t−t0)e−jkw0tdt=1T∫Tx(τ)e−jk(2π/T)(τ+t0)dτ⇐τ=t−t0=1T∫Tx(τ)e−jk(2π/T)τdτ ⋅e−jk(2π/T)t0=e−jk(2π/T)t0 ⋅ak(7)(8)(9)(10) (7) b k = 1 T ∫ T x ( t − t 0 ) e − j k w 0 t d t (8) = 1 T ∫ T x ( τ ) e − j k ( 2 π / T ) ( τ + t 0 ) d τ ⇐ τ = t − t 0 (9) = 1 T ∫ T x ( τ ) e − j k ( 2 π / T ) τ d τ ⋅ e − j k ( 2 π / T ) t 0 (10) = e − j k ( 2 π / T ) t 0 ⋅ a k - 时域相乘 待证明,未完成
假设 x(t) x ( t ) , y(t) y ( t ) 是两个周期为T的周期信号,则乘积 x(t)y(t) x ( t ) y ( t ) 也是周期信号,周期为T.
x(t)↔aky(t)↔bkx(t)y(t)↔hk x ( t ) ↔ a k y ( t ) ↔ b k x ( t ) y ( t ) ↔ h k
ak=1T∫Tx(t)e−jkw0tdt=1T∫Tx(t)e−jk(2π/T)tdtbk=1T∫Ty(t)e−jkw0tdt=1T∫Ty(t)e−jk(2π/T)tdtx(t)=∑k=−∞+∞akejkw0t=∑k=−∞+∞akejk(2π/T)ty(t)=∑k=−∞+∞bkejkw0t=∑k=−∞+∞bkejk(2π/T)t a k = 1 T ∫ T x ( t ) e − j k w 0 t d t = 1 T ∫ T x ( t ) e − j k ( 2 π / T ) t d t b k = 1 T ∫ T y ( t ) e − j k w 0 t d t = 1 T ∫ T y ( t ) e − j k ( 2 π / T ) t d t x ( t ) = ∑ k = − ∞ + ∞ a k e j k w 0 t = ∑ k = − ∞ + ∞ a k e j k ( 2 π / T ) t y ( t ) = ∑ k = − ∞ + ∞ b k e j k w 0 t = ∑ k = − ∞ + ∞ b k e j k ( 2 π / T ) t
hk=1T∫Tx(t)y(t)e−jkw0tdt=1T∫T∑m=−∞+∞amejmw0t ⋅∑n=−∞+∞bnejnw0t ⋅e−jkw0tdt=1T∫T∑m=−∞+∞∑n=−∞+∞ambnej(m+n)w0t ⋅e−jkw0tdt=1T∫T∑m=−∞+∞∑n=−∞+∞ambnej(m+n−k)w0t}dt=1T∫T∑m=−∞+∞∑n=−∞+∞ambnej(m+n−k)w0t}dt(11)(12)(13)(14)(15) (11) h k = 1 T ∫ T x ( t ) y ( t ) e − j k w 0 t d t (12) = 1 T ∫ T ∑ m = − ∞ + ∞ a m e j m w 0 t ⋅ ∑ n = − ∞ + ∞ b n e j n w 0 t ⋅ e − j k w 0 t d t (13) = 1 T ∫ T ∑ m = − ∞ + ∞ ∑ n = − ∞ + ∞ a m b n e j ( m + n ) w 0 t ⋅ e − j k w 0 t d t (14) = 1 T ∫ T ∑ m = − ∞ + ∞ ∑ n = − ∞ + ∞ a m b n e j ( m + n − k ) w 0 t } d t (15) = 1 T ∫ T ∑ m = − ∞ + ∞ ∑ n = − ∞ + ∞ a m b n e j ( m + n − k ) w 0 t } d t
- 时域卷积
- 时域卷积








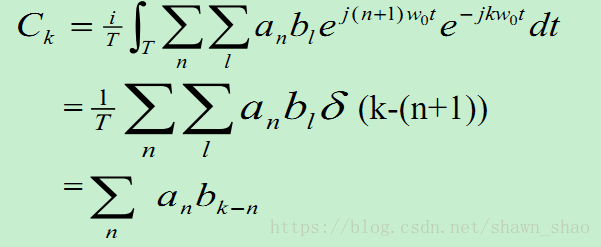














 8万+
8万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








