线性代数之向量基础点

                                    线性代数之向量基础点

向量的定义

由n个按照次序排成的数组成的数组叫n维向量，每个数称为该向量的n的分量，其中第i个数 称为第i个分量。按照行(列)排列的向量叫做行(列)向量。

n维列向量记作: 

几点说明：

• 如果kα=0,这里的0是零向量，k是常数，则要么k=0要么α=0。

 

向量组的定义

向量组：n个同维的行向量(列向量)组成的集合向量组。

向量组与矩阵

m个n维列向量所组成的向量组A：a1  构成了n*m的矩阵,记作A=(a1  ，a2  … am  )

注：这里n维列向量，即可看作行有n个。

m个n维行向量所组成的向量组构成了m*n的矩阵,记作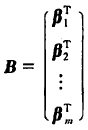

 

线性组合

给定向量组 ,对于任意一组实数 则表达式

则称为向量组A的线性组合。其中叫做该线性组合的系数。

 

线性表示

如果向量   则b是向量组A的线性组合，这是向量b可有向量组A线性表示。这里其实转换为了方程有解，全是0也是有解。

特别的：

• 线性表示时系数可以全是0
• 0向量可有任意向量组表示。
• 任何向量都可由 (1,0,...0),(0,1,0...0),(0,0,1...0) ...(0,0...0...1)表示

向量组等价

两个向量组可以相互线性表示，叫做第一个向量组等价于第二个向量组。向量组等价的性质：

反身性：向量组和自己等价，A～A。

对称性：向量组可以相互等价，A～B则B～A

传递性: 向量组1等价于向量组2，向量组2等价于向量组3则，向量1等价于向量组3，即A～B，B～C则A～C

 

线性相关

向量是n个m维(每个向量分量的个数)的向量，若存在一组不全为0的   使得 则α 是线性相关的，反之线性无关。

线性无关即等价于以下命题：

1. 线性不相关
2. 找不到一组不全0的 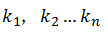   使得
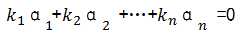
3.  全为0

几种情况:

关于单个向量

• 向量组中两个向量成比例，则两个向量必线性相关
• 含零向量的任向量组必线性相关(取0向量的系数为1或者k，其余均为0)
• 一个零向量必线性相关
• 一个非零向量必然线性无关
• 一个向量线性相关的充要条件是向量为0向量

关于向量组

• 部分组线性相关则整体组也线性相关(这里的部分组是指向量组的部分，即假设向量组有n个向量，则此时部分组是它的 “部分”，即有k个，k小于n)

              逆否命题整体组线性无关 则部分组也线性无关也成立。

• 线性无关的向量组的接长向量组也无关（线性无关的向量组的每个向量按相同位置随机增加一些分量得到的高维向量组也是线性无关的，这里涉及向量组里每个向量的维数即单个向量元素个数。这里的接长即对于于每个向量的维数的增加。

             逆否命题线性相关的向量组截短之后的向量组也线性相关。这里截断时仍保留原有的系数即可(因之前已经找不到不全为0的系数)。

比如 b=(3,0,0,4)， 则 

如果截短，如果须按 则即仍然线性相关。

延展阅读：

• 向量组部分相关则整体组相关的理解：

由定义则取原有系数不变(至少含不全为0系数)，新增的向量(组)系数全部取0即可。(外部部分行代替整体行，可理解成内部有线性关系再外延还是有这个线性关系)

• 逆否命题，整体组线性无关则部分组也线性无关的理解：

由线性无关定义则原系数均为0，则取部分组时也是线性无关。(外部全体不行则部分不行)

• 线性无关的接长向量组也无关的理解：

由线性无关定义则原系数均为0，则向量组里每个向量里新接个元素系数为0时才能满足线性表示的定义，亦无关。(内部无关则扩大后仍无关)

• 线性相关的向量组截短之后的向量组也线性相关的理解:

由定义则取原有系数不变(至少含不全为0系数)，截断的向量(组)系数仍取原有的。(内部相关则缩小后仍相关)

线性相关与方程组

针对n个n维的向量（向量的个数等于向量的维数，向量组的另外中说法）线性无关的充要条件是它的行列式不等于0(齐次方程系数行列式不等于0，必有唯一0解，即系数全为0)，线性相关的充要条件是它的行列式等于0

两点说明:

  线性组合充要条件方程有解(源于线性组合的定义)；

不是线性组合充要条件方程无解。

线性相关的充要条件是方程有非零解（源于线性相关的定义）；

    线性无关的充要条件是方程只有零解。

 

极大无关组

极大无关组

假设有向量组A：a1  ，a2  … am  的部分组和部分组a1  ，a2  … ak  (这里k小于等于m，可从向量组里挑选)满足如下条件：

       1) 部分组之间线性无关

       2) 向量组里每个向量均可由该部分组线性表示。

       3）该向量组的向量个数最大

则成这样的部分向量组为极大线性无关组。

不难发现，极大无关组有如下特点:

1. 任意两个极大无关组含向量个数是相同的。
2. 极大无关组不唯一

极大无关组求解步骤：

   1) 原始矩阵均按照列组成向量

   2) 只应用行变换，形成行简化阶梯型

    3) 首非零元所在列为极大无关组

    4) 其余向量的系数用简化阶梯型按列填充

 

向量组的秩

极大无关组含向量的个数，记作 即称为向量组的秩。

向量秩的特点：

一定小于等于向量的维数，因为当找的向量个数大于维数时线性相关。

向量组的秩大于0小于等于向量个数和向量维数的较小者。min{向量个数,向量维数}