《数据结构》学习笔记——时间复杂度

最新推荐文章于 2024-05-04 05:30:00 发布

呆瓜瓜瓜瓜

最新推荐文章于 2024-05-04 05:30:00 发布

阅读量695

点赞数

1.大O表示法

算法复杂度可以从最理想情况、平均情况和最坏情况三个角度来评估，由于平均情况大多和最坏情况持平，而且评估最坏情况也可以避免后顾之忧，因此一般情况下，我们设计算法时都要直接估算最坏情况的复杂度。大O表示法O(f(n)中的f(n)的值可以为1、n、logn、n²等，因此我们可以将O(1)、O(n)、O(logn)、O(n²)分别可以称为常数阶、线性阶、对数阶和平方阶，那么如何推导出f(n)的值呢？我们接着来看推导大O阶的方法。

推导大O阶，我们可以按照如下的规则来进行推导，得到的结果就是大O表示法：

1.用常数1来取代运行时间中所有加法常数。

2.修改后的运行次数函数中，只保留最高阶项

3.如果最高阶项存在且不是1，则去除与这个项相乘的常数。

常数阶

  int sum = 0,n = 100; //执行一次  
  sum = (1+n)*n/2; //执行一次  
  System.out.println (sum); //执行一次

上面算法的运行的次数的函数为f(n)=3，根据推导大O阶的规则1，我们需要将常数3改为1，则这个算法的时间复杂度为O(1)。如果sum = （1+n）*n/2这条语句再执行10遍，因为这与问题大小n的值并没有关系，所以这个算法的时间复杂度仍旧是O(1)，我们可以称之为常数阶。

线性阶
线性阶主要要分析循环结构的运行情况，如下所示。

for(int i=0;i<n;i++){
//时间复杂度为O(1)的算法
...
}

上面算法循环体中的代码执行了n次，因此时间复杂度为O(n)。

对数阶

int number=1;
while(number<n){
number=number*2;
//时间复杂度为O(1)的算法
...
}

可以看出上面的代码，随着number每次乘以2后，都会越来越接近n，当number不小于n时就会退出循环。假设循环的次数为X，则由2^x=n得出x=log₂n，因此得出这个算法的时间复杂度为O(logn)。

平方阶
下面的代码是循环嵌套：

  for(int i=0;i<n;i++){   
      for(int j=0;j<n;i++){
         //复杂度为O(1)的算法
         ... 
      }
  }

内层循环的时间复杂度在讲到线性阶时就已经得知是O(n)，现在经过外层循环n次，那么这段算法的时间复杂度则为O(n²)。

接下来我们来算一下下面算法的时间复杂度：

  for(int i=0;i<n;i++){   
      for(int j=i;j<n;i++){
         //复杂度为O(1)的算法
         ... 
      }
  }

需要注意的是内循环中int j=i，而不是int j=0。当i=0时，内循环执行了n次；i=1时内循环执行了n-1次，当i=n-1时执行了1次，我们可以推算出总的执行次数为：

n+(n-1)+(n-2)+(n-3)+……+1
=(n+1)+[(n-1)+2]+[(n-2)+3]+[(n-3)+4]+……
=(n+1)+(n+1)+(n+1)+(n+1)+……
=(n+1)n/2
=n(n+1)/2
=n²/2+n/2

根据此前讲过的推导大O阶的规则的第二条：只保留最高阶，因此保留n²/2。根据第三条去掉和这个项的常数，则去掉1/2,最终这段代码的时间复杂度为O(n²)。

其他常见复杂度

除了常数阶、线性阶、平方阶、对数阶，还有如下时间复杂度：
f(n)=nlogn时，时间复杂度为O(nlogn)，可以称为nlogn阶。
f(n)=n³时，时间复杂度为O(n³)，可以称为立方阶。
f(n)=2ⁿ时，时间复杂度为O(2ⁿ)，可以称为指数阶。
f(n)=n!时，时间复杂度为O(n!)，可以称为阶乘阶。
f(n)=(√n时，时间复杂度为O(√n)，可以称为平方根阶。

2.复杂度的比较

下面将算法中常见的f(n)值根据几种典型的数量级来列成一张表，根据这种表，我们来看看各种算法复杂度的差异。

n	logn	√n	nlogn	n²	2ⁿ	n!
5	2	2	10	25	32	120
10	3	3	30	100	1024	3628800
50	5	7	250	2500	约10^15	约3.0*10^64
100	6	10	600	10000	约10^30	约9.3*10^157
1000	9	31	9000	1000 000	约10^300	约4.0*10^2567

从上表可以看出，O(n)、O(logn)、O(√n )、O(nlogn )随着n的增加，复杂度提升不大，因此这些复杂度属于效率高的算法，反观O(2ⁿ)和O(n!)当n增加到50时，复杂度就突破十位数了，这种效率极差的复杂度最好不要出现在程序中，因此在动手编程时要评估所写算法的最坏情况的复杂度。

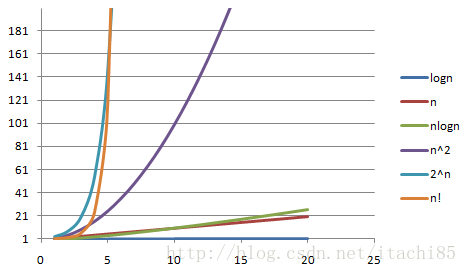
面给出一个更加直观的图：

这里写图片描述

其中x轴代表n值，y轴代表T(n)值（时间复杂度）。T(n)值随着n的值的变化而变化，其中可以看出O(n!)和O(2ⁿ)随着n值的增大，它们的T(n)值上升幅度非常大，而O(logn)、O(n)、O(nlogn)随着n值的增大，T(n)值上升幅度则很小。
常用的时间复杂度按照耗费的时间从小到大依次是：

O(1)<O(logn)<O(n)<O(nlogn)<O(n²)<O(n³)<O(2ⁿ)<O(n!)

3.常用的时间复杂度举例

名称	复杂度类	运行时间（ $T(n)$ ）	运行时间举例	算法举例
常数时间		$O(1)$	10	判断一个二进制数的奇偶
反阿克曼时间		$O(\alpha(n))$		并查集的单个操作的平摊时间
迭代对数时间		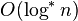$O(\log^{*}n)$		en:Cole-Vishkin algorithm
对数对数时间		$O(\log \log n)$		有界优先队列的单个操作^[1]
对数时间	DLOGTIME	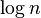$O(\log n)$	$\log n$ ， $\log n^2$	二分搜索
幂对数时间		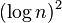$(\log n)^{O(1)}$	$(\log n)^2$
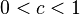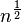（小于1次）幂时间		$O(n^c)$ ，其中 $0 < c < 1$	$n^{\frac{1}{2}}$ ， $n^{\frac{2}{3}}$	K-d树的搜索操作
线性时间		$O(n)$	$n$	无序数组的搜索
线性迭代对数时间		$O(n\log^{*}n)$		Raimund Seidel的三角分割多边形算法
线性对数时间		$O(n\log n)$	$n\log n$ ， $\log n!$	最快的比较排序
二次时间		$O(n^2)$	$n^2$	冒泡排序、插入排序
三次时间		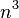$O(n^3)$	$n^3$	矩阵乘法的基本实现，计算部分相关性
多项式时间	P	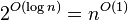$2^{O(\log n)} = n^{O(1)}$	$n$ ， $n \log n$ ， $n^{10}$	线性规划中的en:Karmarkar's algorithm，AKS质数测试
准多项式时间	QP	$2^{(\log n)^{O(1)}}$		关于有向斯坦纳树问题最著名的 $O(\log^2 n)$ 近似算法
次指数时间（第一定义）	SUBEXP	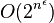$O(2^{n^{\epsilon}})$ ，对任意的ε > 0	$O(2^{(\log n)^{\log \log n}})$	Assuming complexity theoretic conjectures, BPP is contained in SUBEXP.^[2]
次指数时间（第二定义）		2^o(n）	2^{n^1/3}	Best-known algorithm for integer factorization and graph isomorphism
指数时间	E	2^O(n)	1.1ⁿ, 10ⁿ	使用动态规划解决旅行推销员问题
阶乘时间		O(n!)	n!	通过暴力搜索解决旅行推销员问题
指数时间	EXPTIME	2^poly(n)	2ⁿ, 2^n²
双重指数时间	2-EXPTIME	2^{2^poly(n)}	2^2ⁿ	Deciding the truth of a given statement in Presburger arithmetic

呆瓜瓜瓜瓜

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
《数据结构》学习笔记——时间复杂度

1.大O表示法算法复杂度可以从最理想情况、平均情况和最坏情况三个角度来评估，由于平均情况大多和最坏情况持平，而且评估最坏情况也可以避免后顾之忧，因此一般情况下，我们设计算法时都要直接估算最坏情况的复杂度。大O表示法O(f(n)中的f(n)的值可以为1、n、logn、n²等，因此我们可以将O(1)、O(n)、O(logn)、O(n²)分别可以称为常数阶、线性阶、对数阶和平方阶，那么如何推导出f(n...
复制链接

扫一扫