快乐地打牢基础（2）——强连通分量

最新推荐文章于 2022-08-23 17:08:20 发布

Miserable_ccf

最新推荐文章于 2022-08-23 17:08:20 发布

阅读量333

点赞数 2

分类专栏：快乐图论快乐打牢基础

本文链接：https://blog.csdn.net/sinat_40872274/article/details/99344104

版权

快乐打牢基础同时被 2 个专栏收录

13 篇文章 3 订阅

订阅专栏

快乐图论

8 篇文章 1 订阅

订阅专栏

一、定义

在有向图 ${G}$ 中，如果两个顶点 ${u,v}$ 间尊在一条 ${u}$ 到 ${v}$ 的路径且也存在一条 ${v}$ 到 ${u}$ 的路径，则称这两个顶点 ${u，v}$ 是强联通的（strongly
connected）。如果有向图 ${G}$ 是一个强连通图，有向非强连通图的极大强连通子图，称为强连通分量（strongly connected components）。

极大强连通子图： ${G}$ 是一个极大强连通子图，当且仅当 ${G}$ 是一个强连通子图且不存在另一个强连通子图 ${G'}$ ，使得 ${G}$ 是 ${G'}$ 的真子集。

举个例子：
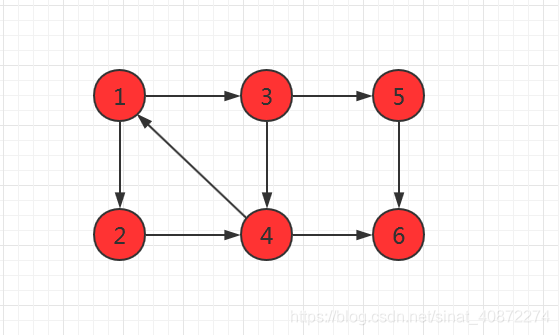
在下图中，子图 ${\{1,2,3,4\}}$ 是一个强连通分量，因为顶点 ${1,2,3,4}$ 两两可达， ${\{5\},\{6\}}$ 也是两强连通分量。
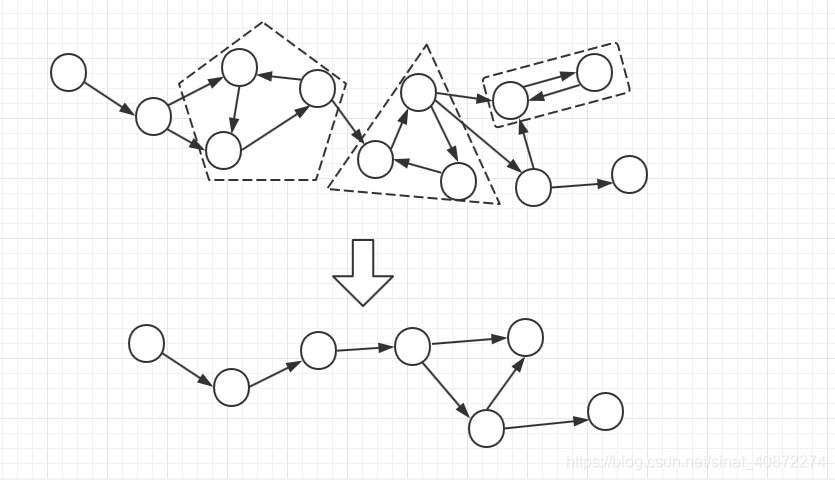
在这里插入图片描述
应用：若将原图所有的强连通分量都缩为一个点，那么原图就会形成一个DAG(有向无环图)

在这里插入图片描述

二、Kosaraju算法

基于两次DFS的有向图强连通子图的算法。时间复杂度 ${O(n+m)}$

算法过程：
Ⅰ.对原有向图 ${G}$ 进行DFS，记录结点访问完的顺序 ${d[i]}$ , ${d[i]}$ 表示第 ${i}$ 个访问完的结点是 ${d[i]}$ 。

Ⅱ.选择具有最晚访问完的顶点，对反向图 ${GT}$ 进行DFS，删除能够遍历到的顶点，这些顶点构成一个强连通分量。

Ⅲ.如果还有顶点没有删除，继续第二步，否则算法结束。

举个栗子：
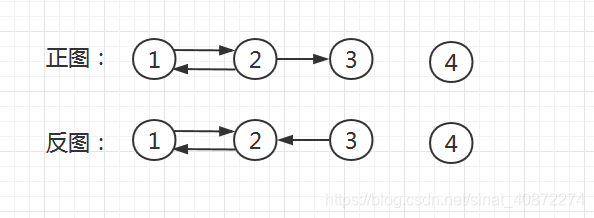
在这里插入图片描述
第一次遍历的访问次序是1,2,3,4；访问完成的顺序是3,2,1,4.。

第二次遍历是按照“访问完成的顺序”从后向前访问，所以第二次是先从4开始，然后是1,2，最后是3。

最后我们可以求出三个强连通分量： ${\{(4),(1,2),(3)\}}$ 。

算法模板：

#include<bits/stdc++.h>
using namespace std;

const int Max = 101;
int vis[Max]={0},mapp[Max][Max],d[Max],n,t=0;
void dfsone(int x) {
	vis[x] = 1;
	for(int i = 1; i <= n; i++) {
		if(!vis[i] && mapp[x][i]) dfsone(i);
	}
	d[++t] = x;
}
void dfstwo(int x) {
	vis[x] = t;
	for(int i = 1; i <= n; i++)
		if(!vis[i] && mapp[i][x]) dfstwo(i);
}

void Kosaraju() {
	int i;
	t = 0;
	//进行第一次DFS遍历
	for(i = 1; i<= n; i++)
		if(!vis[i]) dfsone(i);
	memset(vis,0,sizeof(vis));
	t = 0;
	printf("\nd[i]:\n");
	for(int i = 1; i <= n; i++)
		printf("%d ",d[i]);
	//进行第二次DFS遍历

	for(i = n; i >= 1; i--)
		if(!vis[d[i]]) {
			t++;
			dfstwo(d[i]);
		}
	printf("\nt = %d\n",t);
}
int main() {
	scanf("%d",&n);
	//使用邻接矩阵存储
	for(int i = 1; i <= n; i++) {
		getchar();
		for(int j = 1; j <= n; j++)
			scanf("%d",&mapp[i][j]);
	}
	Kosaraju();
		printf("\nvis[i]:\n");
	for(int i = 1; i <= n; i++)
		printf("%d ",vis[i]);
	return 0;
}
/*
4
0 1 0 0
1 0 1 0
0 0 0 0
0 0 0 0

*/

上述例子的运行结果:
在这里插入图片描述

三、Tarjan算法

1.一些概念和定义

Tarjan算法，由罗伯特·塔扬（Robert Tarjan）提出，是基于对图深度优先搜索（DFS）的算法，每个强连通分量为搜索树的一棵子树。搜索时，把当前搜索树中未处理的结点加入到一个栈，回溯时可以判断栈顶到栈中的结点是否构成一个强连通分量。

DFS过程中会遇到的四种边：

树枝边：DFS时经过的边，即DFS搜索树上的边
前向边：与DFS方向一致，从某个结点指向其某个子孙的边
后向边：与DFS方向相反，从某个结点指向其某个祖先的边
横叉边：从某个结点指向搜索树中另一子树中某结点的边

定义 ${DFN（u）}$ 为结点 ${u}$ 的搜索次序编号（时间戳）， ${Low（u）}$ 为 ${u}$ 或者 ${u}$ 的子树能够回溯到的最早的栈中结点的DFN值，也就是点 ${u}$ 及其子孙结点的中最小的DFN值。

由上面四种边的定义可以得到：

如果 ${(u,v)}$ 为树枝边， ${u}$ 为 ${v}$ 的父结点，则 ${Low（u） =Min\{Low(u),Low(v)\}}$

如果 ${(u,v)}$ 为后向边或者指向栈中的结点的横叉边，则 ${Low（u）=Min\{Low(u),DFN(v)\}}$

当结点 ${u}$ 的搜索过程结束后，若 $D F N (u) = L o w (u)$ ，则以 ${u}$ 为根的搜索子树上所有还在栈中的结点（即 ${u}$ 和栈中在 ${u}$ 之后的所有结点）是一个强连通分量，可退栈。为什么呢？通俗地说，若 ${u}$ 为强连通分量的根，那么它的子孙中最高祖宗就是它本身。

2.算法的主要过程

数组初始化：当首次搜索到点 ${u}$ 时， ${DFN(u)}$ 为结点 ${u}$ 的搜索次序编号（时间戳）。
堆栈：将 ${u}$ 压入栈顶。
更新 ${Low(u)}$ ：
如果 ${(u,v)}$ 为树枝边（ ${v}$ 不在栈中）， ${u}$ 为 ${v}$ 的父结点，则 ${Low（u）= Min\{Low(u),Low(v)\}}$ 。

如果 ${(u,v)}$ 为后向边或者指向栈中结点的横叉边（ ${v}$ 在栈中），则 ${Low（u）=Min\{Low(u),DFN(v)\}}$
如果 ${u}$ 的子树已经全部遍历后 ${Low(u) = DFN(u)}$ ，则将 ${u}$ 和栈中在 ${u}$ 之后的所有结点弹出栈。这些出栈的元素组成一个强连通分量。
继续搜索（或许会更换搜索的起点，因为整个有向图可能分为多个不连通的部分），直到所有的点被遍历。

3.算法流程演示

下面直接用例子来演示算法过程，更为直观。
先复习一下定义：

树枝边：DFS时经过的边。
前向边：与DFS方向一致，从某个结点指向其某个子孙的边。
后向边：与DFS方向相反，从某个结点指向其某个祖先的边。
横叉边：从某个结点指向搜索树中另一子数中的某结点的边。
DFN（ ${u}$ ）：结点 ${u}$ 的搜索次序编号（时间戳）。
Low（ ${u}$ ）： ${u}$ 或者 ${u}$ 的子树能够回溯到的最早的栈中结点的DFN值。

从结点1开始DFS
从1进入 DFN［1］＝ Low［1］＝＋＋cnt = 1
入栈 1
由1进入3 DFN［3］＝Low［3］＝＋＋cnt = 2
入栈 1 3
之后由2进入5 DFN［4］＝Low［5］＝＋＋cnt = 3
入栈 1 3 5
之后由4进入 6 DFN［6］＝Low［6］＝＋＋cnt = 4
入栈 1 3 5 6
栈中结果是 $\rightarrow3 \rightarrow5 \rightarrow6}$ 。搜索到结点 ${u = 6}$ 时，DFN[6]= Low[6]，找到一个强连通分量。将 ${u}$ 和 ${u}$ 后面所有结点弹出栈，因为 ${u}$ 后面没有元素，弹出 ${u}$ ， ${\{6\}}$ 为一个强连通分量。
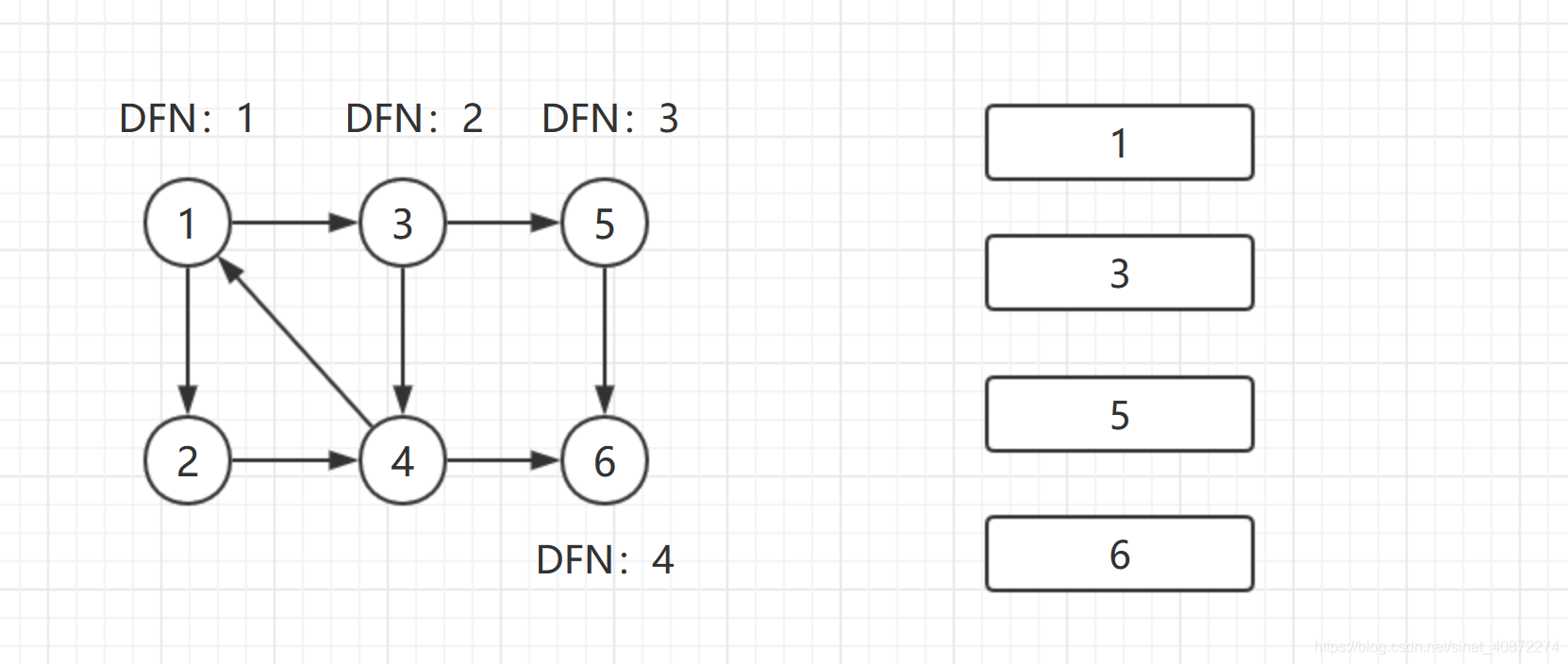
在这里插入图片描述
返回结点5，发现DFN[5] = Low[5]，退栈后， ${\{5\}}$ 为一个强连通分量。
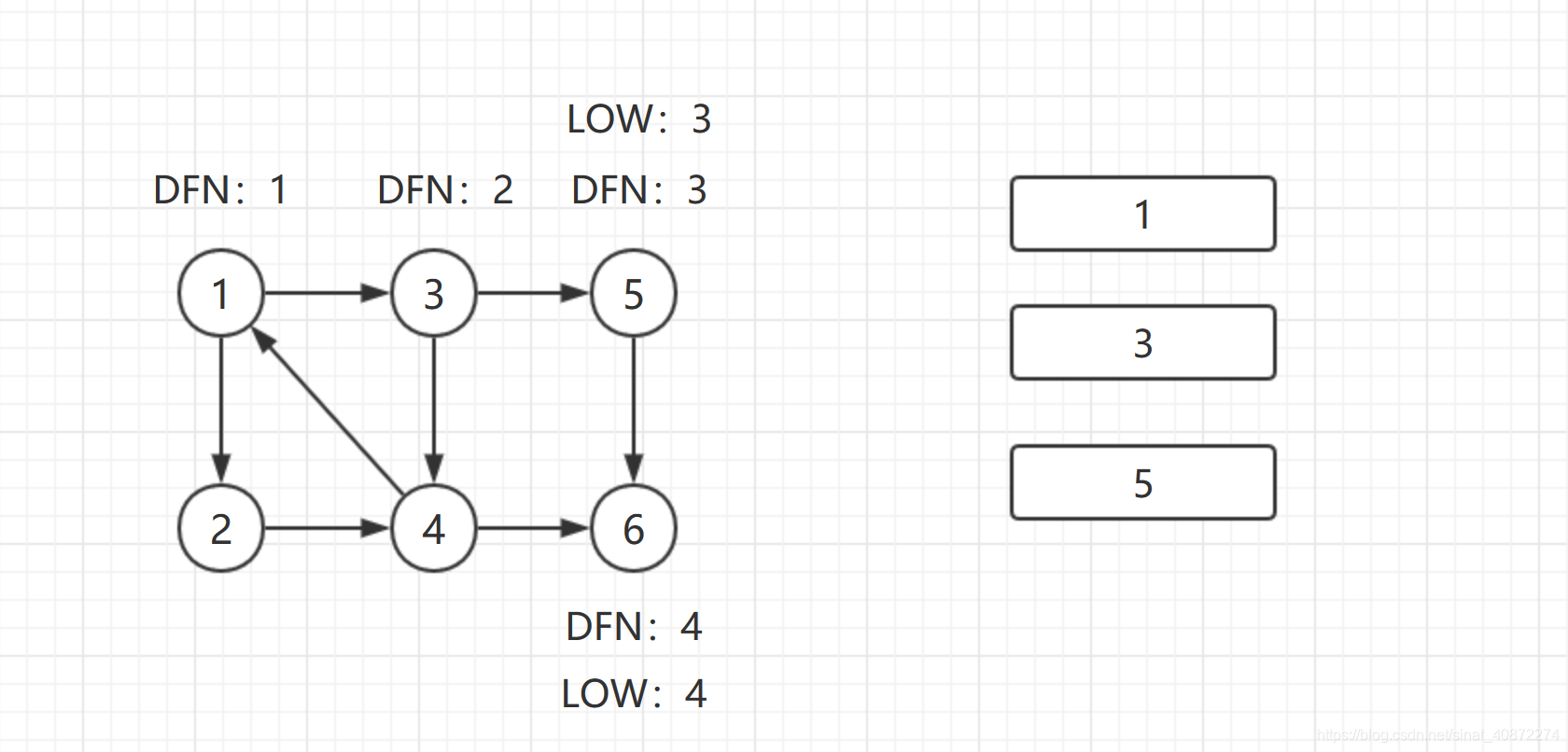返回结点3，继续搜索，到达结点4，把4加入栈。发现结点4向结点1有后向边，结点1还在栈中，所以 ${Low[4] = Min\{Low(4),DFN(1)\} = 1}$ 。结点6已经出栈，（4,6）是指向非栈中结点的横叉边，因此不更新 ${Low[4]}$ 返回3，（3,4）为树枝边，所以 ${Low[3] = Min\{Low[3],Low[4]\}}$ 。
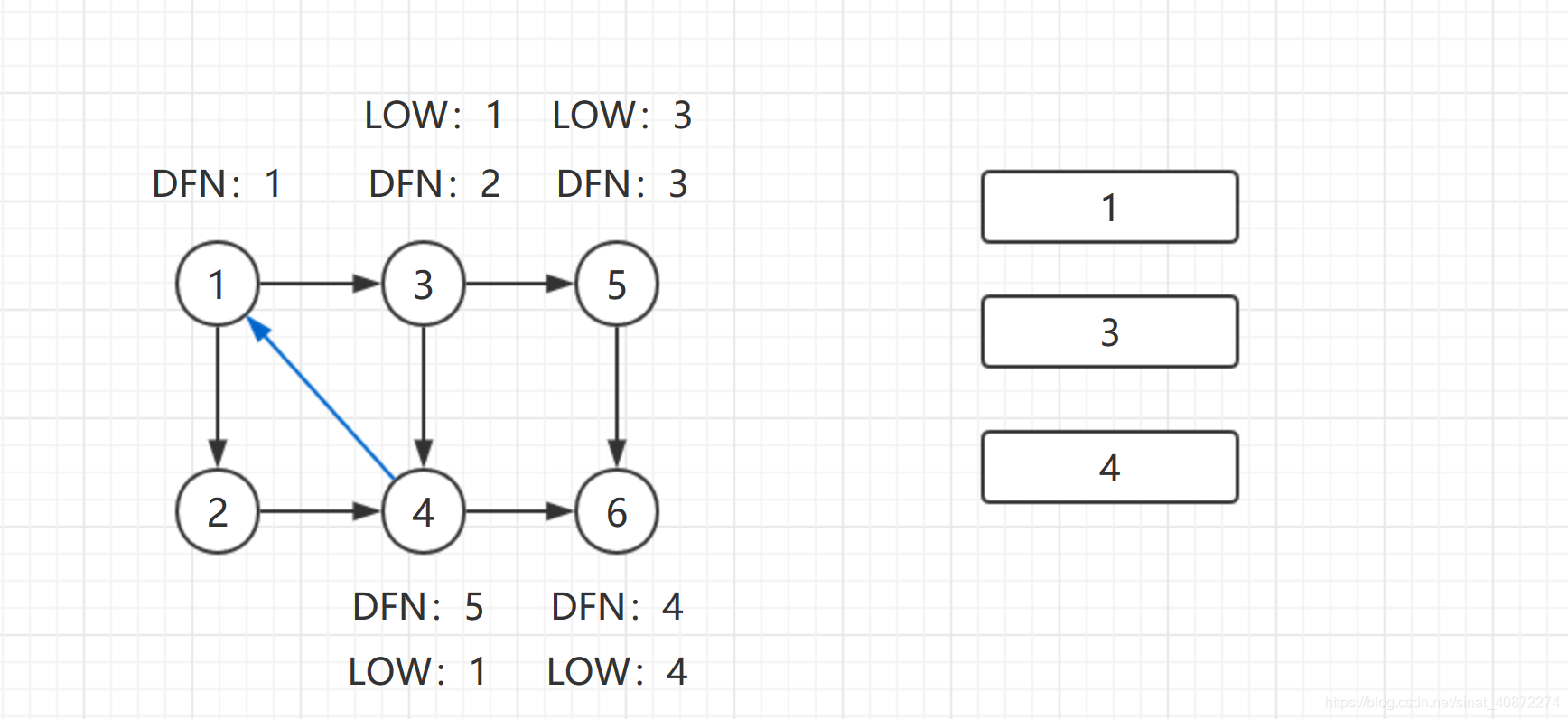在这里插入图片描述继续回到结点1，最后访问结点2。访问边（2,4）此边是指向栈中结点的横叉边，4还在栈中，所以 ${Low[2] = Min\{Low[2],DFN[4]\} = 5}$ .返回1后，发现 ${DFN[1] = Low[1]}$ ，把栈中1及以后的所有结点弹出，组成一个强连通分量 ${\{1,3,4,2\}}$ 。
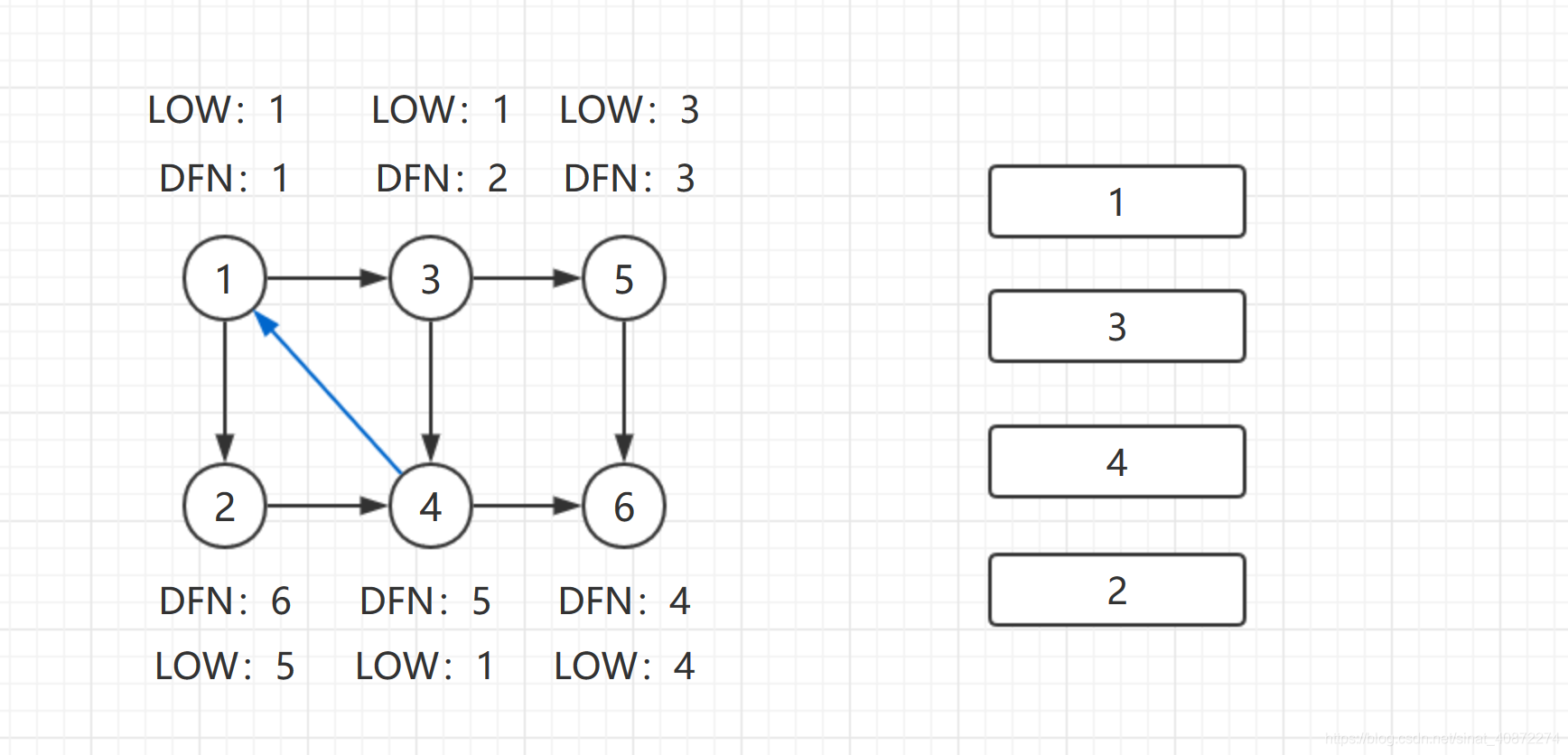
在这里插入图片描述

到此，算法结束。一共求出了三个强连通分量 ${\{6\},\{5\},\{1,3,4,2\}}$ 。

在运行Tarjan算法的过程中，每个顶点被访问了一次，且只进出一次栈，每条边也只访问了一次，所以该算法的时间复杂度为 ${O(n+m)}$ ，n为点数，m为边数。
模板代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e4+10;
const int M = 5e4+10;
vector<int> G[M];
//  sta ：栈     bk[u] : 结点u是否在栈中  dfn和low如提议描述
//  top是栈顶  col是染色标记  cnt：计数   n：点个数  m：边个数 
int dfn[N],low[N],sta[N],bk[N],cnt,top,color = 0;
int n,m;
void Tarjan(int u){
	dfn[u] = low[u] = ++cnt;//打上时间戳 并初始化low 
	sta[++top] = u;//u入栈
	int len = G[u].size(); 
	for(int i = 0 ; i < len; i++){
		int v = G[u][i];
		if(!dfn[v]){//如果后继点没有访问过就从后继点开始继续搜索 
			Tarjan(v);
			low[u] = min(low[u],low[v]);//树枝边，更新low[u] 
		}else if(!bk[v]){//若v在栈中 
			low[u] = min(low[u],dfn[v]); //后向边或者指向栈内结点的横叉边 
		}
	}
	if(low[u] == dfn[u]){
		bk[u] = ++color;
		while(sta[top] != u){
			bk[sta[top]] = color;//将sta[top]弹出，并染色为color 
			--top;
		}
		--top;//将u弹出 
	}
} 
int main(){
	scanf("%d %d",&n,&m);
	int x,y;
	for(int i = 1; i <= m; i++){
		scanf("%d %d",&x,&y);
		G[x].push_back(y);
	}
	for(int i = 1; i <= n; i++)
		if(!dfn(i))
			Tarjan(i);
	for(int i = 1; i <= n; i++)
		cout<<bk[i]<<" "; 
	return 0;
}
/*
6 8
1 2
1 3
2 4
3 4
3 5
4 1
4 6
5 6
*/

4.操作原理

Tarjan算法的操作原理如下：
Tarjan算法基于定理：在任何DFS中，同一强连通分量内的所有顶点均在同一棵深度优先搜索树中。 也就是说，强连通分量一定是有向图的某一棵深度优先搜索树的子树。

可以证明，当一个点既是强连通子图Ⅰ中的点，又是强连通子图Ⅱ中的点时，它是强连通子图Ⅰ ${\bigcup}$ 图Ⅱ中的点。

这样，我们用Low值记录该点所在强连通子图对应的搜索子树的根结点的DFN值。注意，该子树中的元素在栈中一定是相邻的，且根结点在栈中一定位于所有子树元素的最下方。

强连通分量是由若干个环组成的。所以，当有环形成时（也就是搜索的下一个点已在栈中），我们将这一条路的Low值统一，即这条路径上的点属于同一个强连通分量。

如果遍历完整棵搜索树后，某个点的DFN的值等于Low的值，则它是该搜索子树的根。 这时，它以上（包括它自己）一直到栈顶的所有元素组成一个强连通分量。

四、Tarjan算法的用途

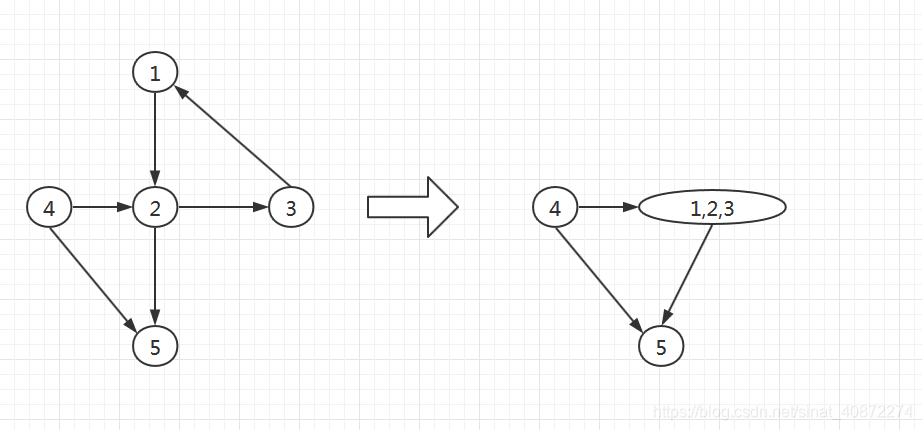
1.有向图的缩点

将同一个强连通分量中的点缩成一个新结点，对于两个新节点 ${a,b}$ ，它们之间有边相连，当且仅当存在两个点 ${u}$ 属于 ${a}$ ， ${v}$ 属于 ${b}$ ，且 ${<u,v>\in E}$ 。
在这里插入图片描述

2.解决2-SAT问题

通俗的sat问题表述一般是这样的：有很多个集合，每个集合里面有若干元素，现给出一些取元素的规则，要你判断是否可行，可行则给出一个可行方案。如果所有集合中，元素个数最多的集合有k个，那么我们就说这是一个k-sat问题，同理，2-sat问题就是k=2时的情况。
（摘自博客：https://blog.csdn.net/hawo11/article/details/74908233）
【例题】一本通 OJ 1513 （BZOJ 1051） USACO 2003 Fall 受欢迎的牛
题意：

有 N 头牛，给你 M 对整数 (A,B)，表示牛 A 认为牛 B 受欢迎。这种关系是具有传递性的，如果 A 认为 B 受欢迎，B 认为 C 受欢迎，那么牛 A 也认为牛 C 受欢迎。你的任务是求出有多少头牛被除自己之外的所有牛都认为是受欢迎的。

思路：

这题的思路就比较简单

把牛看成点，把“认为受欢迎”的这种关系变成一条有向边，A认为B受欢迎,那么A ${\rightarrow}$ B，形成一个有向图。

因为受欢迎有传递性，所以在有向图上找出强连通子图，可以知道每个子图中的牛一定是互相喜欢的（子图中的任意一头牛都可以被子图内的其他牛喜欢），把每一个强连通子图找出来，缩点，然后整个图就变成有向无环图（DAG）。因为一头牛需要受到其他所有牛的欢迎，那么它就不能喜欢任意除了自己这个连通子图的其他牛。

所以，找到一个出度为0的强连通子图（此时应该已经缩成了一个点），其中的牛的头数就是需要的答案，当然如果存在两个及两个以上的出度为0的点，那就说明这几个子图中的奶牛各自无法欢迎其他子图里的奶牛，输出0。
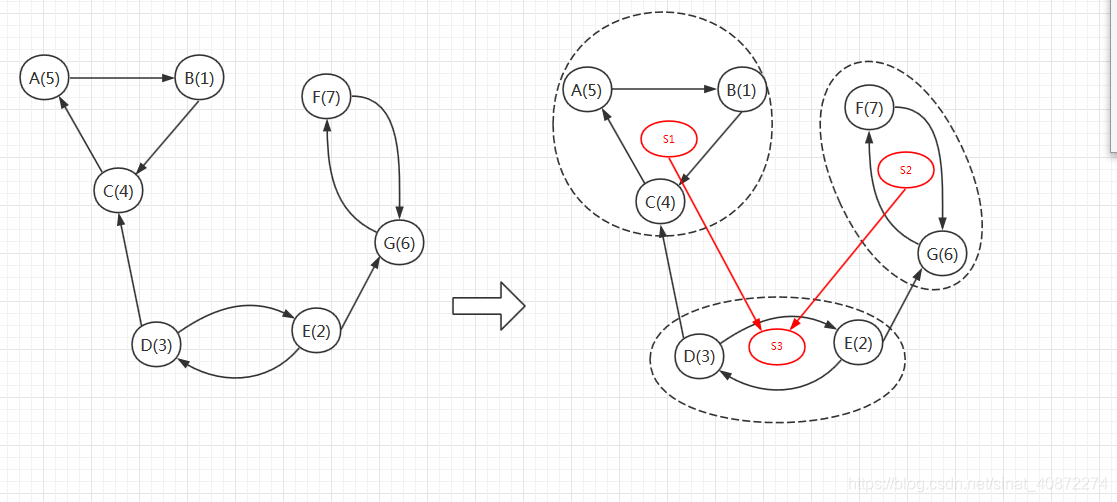
如下图举例
D和E就是所有牛都欢迎的。
在这里插入图片描述

#include <bits/stdc++.h>
using namespace std;

const int N = 1e4 + 10;
const int M = 5e4 + 10;
vector<int> G[M];
//de[i]:表示强连通子图i的出度  si[i]:表示 强连通子图i中的结点个数 
int dfn[N],low[N],bk[N],sta[N],de[N],si[N];
int n,m,cnt = 0,top,color=0,x,y;
void Tarjan(int u){
	dfn[u] = low[u] = ++cnt; 
	sta[++top] = u;
	int len = G[u].size();
	for(int i = 0 ; i < len; i++){
		int v = G[u][i];
		if(!dfn[v]){
			Tarjan(v);
			low[u] = min(low[u],low[v]);
		}else if(!bk[v]){
			
			low[u] = min(low[u],dfn[v]);
			
		}
	}
	if(low[u] == dfn[u]){
		bk[u] = ++color;
		++si[color];
		while(sta[top] != u){
			++si[color];
			bk[sta[top]] = color;
			--top;
		}
		--top;
	}
}
int main(){
	scanf("%d %d",&n,&m);
	for(int i = 0; i < m; i++){
		scanf("%d %d",&x,&y);
		G[x].push_back(y);// 建图 
	} 
	for(int i = 1; i <= n; i++)
		if(!dfn[i])
			Tarjan(i);
	//进行出度统计 
	for(int i = 1; i <= n ; i++){
		int len = G[i].size();
		for(int j = 0; j < len; j++){
			if(bk[i] != bk[G[i][j]])
				de[bk[i]]++;
		}
	}
	//计算出度为0的强连通子图的个数 
	int ans = 0,u = 0;
	for(int i = 1; i <= color; i++)
		if(!de[i]){ 
			ans = si[i];
			u++;//出度为0的强连通子图的个数 
		} 
	if(u == 1)
		printf("%d\n",ans);
	else
		printf("0\n");
	
	return 0;
}

练习题：一本通OJ

1515 网络协议
1516 消息的传递
1517 间谍网络
1518 抢掠计划
1519 和平委员会

本文完全照抄参考黄新军董永建《信息学奥赛一本通·提高》

Miserable_ccf

关注

2
点赞
踩
1

收藏

觉得还不错? 一键收藏
2
评论
快乐地打牢基础（2）——强连通分量

一、定义在有向图G{G}G中，如果两个顶点u,v{u,v}u,v间尊在一条u{u}u到v{v}v的路径且也存在一条v{v}v到u{u}u的路径，则称这两个顶点u，v{u，v}u，v是强联通的（stronglyconnected）。如果有向图G{G}G是一个强连通图，有向非强连通图的极大强连通子图，称为强连通分量（strongly connected components）。极大强连通子图...
复制链接

扫一扫