蒟蒻的图论总结（2）：用Floyd、Dij.和SPFA解决最短路

（特别感谢zrt大佬对本节目的大力滋磁）

讲完了图论的一些基本知识，我们也可以开始我们在图论海洋的畅游啦，当然现在要首先解决的是多年以来困扰NOIP图论界的基础问题：最短路

提起最短路，各位大佬们首先想到的肯定就是SPFA，然而实际上，作为一个PJ蒟蒻，我想到的就是时间复杂度为O（n^3），空间复杂度最少为O（n^2）的Floyd

无论如何，我们从头讲过

首先来讲讲最短路的分类：

最短路分为单源最短路和多源最短路两类：

        ·单源最短路：从一个点到每一个点的最短路径

        ·多源最短路：每两个点之间的最短路径

好了，然后我们来讲上述的第一种算法：Floyd

        Floyd,也称Warshall算法，是一种用DP来解决最短路的一种算法，此算法因为不需要使用邻接表，仅需邻接矩阵，而受到广大蒟蒻们的喜爱

        dp[i][j][k]表示从j到k只经过前i个点所得的最短路

        转移如下：

dp[i][j][k]=min(dp[i-1][j][i]+dp[i-1][i][k],dp[i-1][j][k]);

        

        由于dp[i][j][k]仅仅由dp[i-1][j][k]，dp[i-1][j][i]和dp[i-1][i][k]有关，所以可以省掉第一维

        因为Floyd用了特殊方法，所以n最大仅仅可能为300，否则会面临TLE或者RE的危险

附上代码：

int g[][];
int d[][];
memset(d,0x3f,sizeof d);
for(int i=1;i<=n;i++){
	for(int j=1;j<=n;j++){
		d[i][j]=min(d[i][j],g[i][j])
	}
}
for(int i=1;i<=n;i++)
	for(int j=1;j<=n;j++)
		for(int k=1;k<=n;k++)
	d[j][k]=min(d[j][k],d[j][i]+d[i][k]);
d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
for(int i=1;i<=n;i++)
	for(int j=1;j<=n;j++)
		for(int k=1;k<=n;k++)
			f[j][k]|=f[j][i]+f[i][k];

在讲Dij.算法之前，我们还是再来讲讲邻接表：

        邻接表所需要的，是以下几个数组：

int  head[N],to[M],nxt[M],w[M],tot;

        以上的四个数组，便是Dij.算法和SPFA算法所需的，至于他们的用处如下：

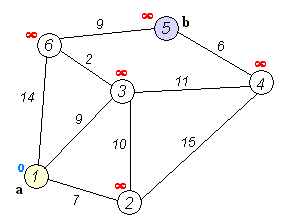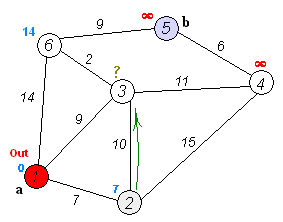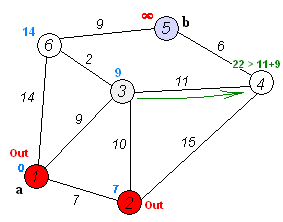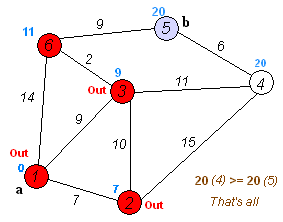
        首先给出一张图：

        上图为Dij.算法的全过程，利用这张图，我们来讲解

        举个栗子，“1”点与“2”、“3”、“6”点均有边相连，假设说head[1]=x，nxt[x]=y，那么to[y]=2或者3或者6，也就是说，上面的tot是当时的边数，而to[nxt[head[x]]]=y代表从x到y之间有一条边权为w[to[nxt[head[x]]]]]的边...

是不是很麻烦...

        说的通俗一点，运用打比方的说明手法，把每个点都当做是一个超大的火车站，这样一来有n个火车站，而每个火车站必然有一个入口，就是head[x]，同时，每个车站必然会有出站口，比如上图，“1”点的第一个点为“2”，也就是说1到2有一个出站口，而那个出站口恰好在火车站的入口旁边（不需要nxt），因为火车站太大，所以在火车站里，有一辆小列车，从head[1]也就是第一个出站口开到第3个出站口，而每一个出站口的名字就是to，车票价格为w

好了也就是这样，我们可以开始我们的加边工程了:

int  head[N],to[M],nxt[M],w[M],tot;
void add(int x,int y,int z){//
	++tot;
	to[tot]=y;
	w[tot]=z;
	nxt[tot]=head[x];
	head[x]=tot;
}

（add(x,y,z)表示从x到y有一条边权为w的边）

现在，我们来总结Dij.算法的精髓：

就是：

贪心！！！

嗯，你没看错，一部世人皆知的算法竟用的是贪心：从所有点中找到dis[i]值最小的顶点i并标记，随后松弛与i相连的所有顶点，以此反复直到所有点都被标记

附上代码：

#include<queue>
struct N{
	int x,w;
	N(int a=0,int b=0){
		x=a,w=b;
	}
	friend bool operator <(N a,N b){
		return a.w>b.w;
	}
}
priority_queue<N> pq;
bool vis[N];
int d[N];
memset(d,0x3f,sizeof d);
d[s]=0;
pq.push(N(s,0));
while(!pq.empty()){
	int x=pq.top().x;pq.pop();
	if(vis[x]) continue;
	vis[x]=1;
	for(int i=head[x];i;i=nxt[i]){
		if(d[to[i]]>d[x]+w[i]){
			d[to[i]]=d[x]+w[i];
			pq.push(N(to[i],d[to[i]]));
		}
	}
}

接下来我们来讲SPFA（队列优化的Bellman-Ford[贝尔曼·福德]）算法：

        与Dij.的思路类似，SPFA的核心同样是贪心：

            1.将源点（S）入队

            2.从队头中取出队头的点v，用源头到v的最短距离来更新源头到v相邻点的最短距离（松弛操作）

            3.将最短距离更新过且本身就不在队列中的点入队

            4.重复第2步知道队列为空

时间复杂度为：O（(n+m) log (n+m)）

附上代码：

#include<queue>


queue<int> q;


memset(d,0x3f,sizeof d);
q.push(s);
d[s]=0;
bool inq[];//是否已经在队列中
while(!q.empty()){
	int x=q.front();q.pop();
	inq[x]=0;
	for(int i=head[x];i;i=nxt[i]){
		if(d[to[i]]>d[x]+w[i]){
			d[to[i]]=d[x]+w[i];
			if(!inq[to[i]]){
				q.push(to[i]);
				inq[to[i]]=1;
			}
		}
	}
}

但是相对于Dij.算法，SPFA算法边权可出现负值，所以它在图论的最短路中仍使用较多，而它的复杂度几乎为O（km）[k为一个2左右的常数]，但是可能会被一些特殊的构造而卡成m^2，它在稀疏图中效率较高

以上便是本章的全部内容，下一部分我也不知道该讲什么好呢...