转载一下牛顿法求解，抽时间再理解一次

原文作者链接，侵删：https://blog.csdn.net/xyz599/article/details/53212848

 

 

平时经常看到牛顿法怎样怎样，一直不得要领，今天下午查了一下维基百科，写写我的认识，很多地方是直观理解，并没有严谨的证明。在我看来，牛顿法至少有两个应用方向，1、求方程的根，2、最优化。牛顿法涉及到方程求导，下面的讨论均是在连续可微的前提下讨论。

 

1、求解方程。

并不是所有的方程都有求根公式，或者求根公式很复杂，导致求解困难。利用牛顿法，可以迭代求解。

原理是利用泰勒公式，在x0处展开，且展开到一阶，即f(x) = f(x0)+(x－x0)f'(x0)

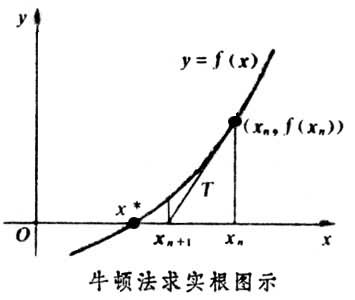
求解方程f(x)=0，即f(x0)+(x-x0)*f'(x0)=0，求解x = x1=x0－f(x0)/f'(x0)，因为这是利用泰勒公式的一阶展开，f(x) = f(x0)+(x－x0)f'(x0)处并不是完全相等，而是近似相等，这里求得的x1并不能让f（x）=0，只能说f(x1)的值比f(x0)更接近f（x）=0，于是乎，迭代求解的想法就很自然了，可以进而推出x(n+1)=x(n)－f(x(n))/f'(x(n))，通过迭代，这个式子必然在f（x*）=0的时候收敛。整个过程如下图：

 

2、牛顿法用于最优化

在最优化的问题中，线性最优化至少可以使用单纯行法求解，但对于非线性优化问题，牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f，求函数f的极大极小问题，可以转化为求解函数f的导数f'=0的问题，这样求可以把优化问题看成方程求解问题（f'=0）。剩下的问题就和第一部分提到的牛顿法求解很相似了。

这次为了求解f'=0的根，把f（x）的泰勒展开，展开到2阶形式：

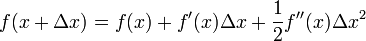
这个式子是成立的，当且仅当 Δx 无线趋近于0。此时上式等价与：

求解：

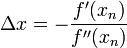
得出迭代公式：

一般认为牛顿法可以利用到曲线本身的信息，比梯度下降法更容易收敛（迭代更少次数），如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

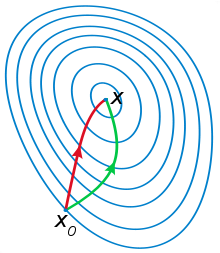
在上面讨论的是2维情况，高维情况的牛顿迭代公式是：

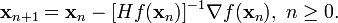
其中H是hessian矩阵，定义为：

 

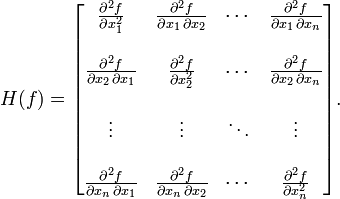
高维情况依然可以用牛顿迭代求解，但是问题是Hessian矩阵引入的复杂性，使得牛顿迭代求解的难度大大增加，但是已经有了解决这个问题的办法就是Quasi-Newton methond，不再直接计算hessian矩阵，而是每一步的时候使用梯度向量更新hessian矩阵的近似。

 

第一个例子

 

求方程f(x) = cos(x) ? x3的根。两边求导，得f '(x) = ?sin(x) ? 3x2。由于cos(x) ≤ 1（对于所有x），以及x3 > 1（对于x>1），可知方程的根位于0和1之间。我们从x0 = 0.5开始。

第二个例子

牛顿法亦可发挥与泰勒展开式，对于函式展开的功能。

求a的m次方根。

xm - a= 0

设f(x) = xm ? a，f'(x) = mxm ? 1

而a的m次方根，亦是x的解，

以牛顿法来迭代：

 

(或 )

 

 

square root by Newton method

 

转自 点击打开链接 

        点击打开链接